타일링(tiling) 문제- 다이나믹 프로그래밍

프로그래머스 2 x n 타일링

세로 길이 2, 가로 길이 n인 2 x n 보드가 있습니다. 2 x 1 크기의 타일을 가지고 이 보드를 채우는 모든 경우의 수를 리턴해야 합니다.
(n은 1 이상 자연수)

return 밑에 console.log(solution(60000)); 을 적으면 통과되고, 안적으면 런타임 에러로 통과가 안된다. (맞은 거 맞겠지..?🤔)

제한사항

• 가로의 길이 n은 60,000이하의 자연수 입니다.
• 경우의 수가 많아 질 수 있으므로, 경우의 수를 1,000,000,007으로 나눈 나머지를 return해주세요.

입출력 예시

let output = tiling(2);
console.log(output); // --> 2
output = tiling(4);
console.log(output); // --> 5

처음에 이 문제가 왜 재귀함수인지도 이해가 안돼서 그림으로 그렸다. 😂
재귀함수 문제라는 것만 이해하면, 그 뒤 풀이는 그렇게 어렵진 않은 편...

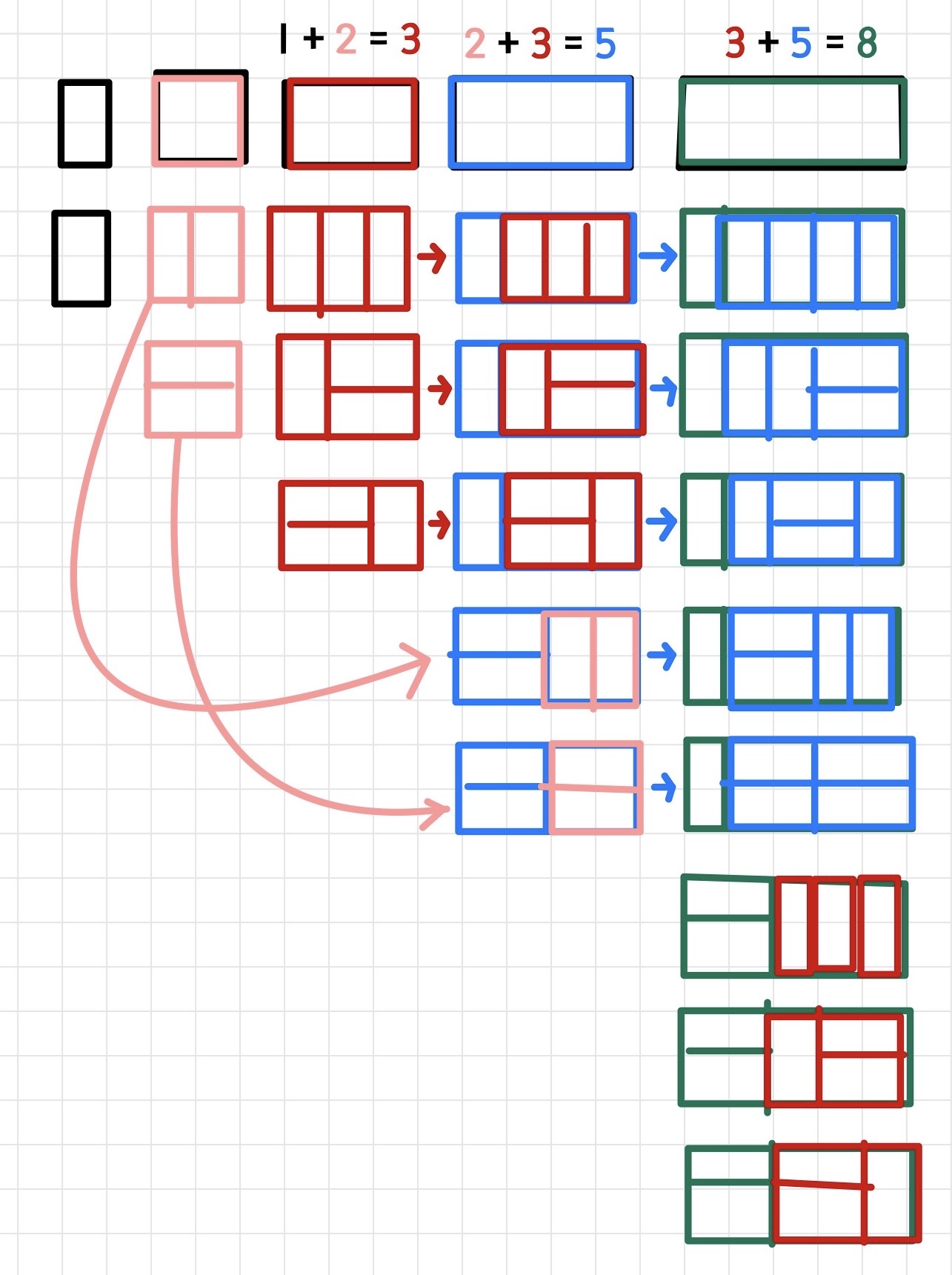
풀이 1. 재귀함수 + 메모이제이션(memoization)

정확성 테스트는 통과하지만, 효율성 테스트는 런타임 에러로 통과하지 못한다.

let tiling = function (n) {
  let memo = [0, 1, 2];
  const func = (size) => {
    if (memo[size]) return memo[size];
    memo[size] = func(size - 2) + func(size - 1);
    return memo[size];
  };
  return func(n);
};

❓ 궁금한 점 - 알고리즘 스터디에서 물어볼 것

프로그래머스 문제에서 왜 return return memo[n] % 1000000007; 이 아닌,
memo[size] = (memo[size - 2] + memo[size - 1]) % 1000000007; 로 풀어야 하는지 좀 이해가 안된다.

memo[size] = (memo[size - 2] % 1000000007) + (memo[size - 1] % 1000000007);
구하려는 경우의 수가 이전 경우의 수를 1000000007로 나눈 나머지들의 합인게 맞는 건가..?

❗️ 궁금증 해결

자바스크립트의 자료형 숫자는 아주 큰 수에 대해 한계점이 존재하고, 아주 큰 수들의 계산에 대한 계산 속도가 느려질 수 있어서 1,000,000,007로 나눈 값의 나머지의 합을 memo 배열에 넣어주게 되는데,

나눠서 몫이 있는 계산이라면 나눠서 더한 결과와 결과를 나눈 값이 달라지겠지만

let x = (10 % 7) + (20 % 7); // x = 9
let y = (10 + 20) % 7 // y = 2
x !== y

문제의 조건에서 n은 60,000이하의 자연수 이고 나누는 값은 1,000,000,007 으로 몫이 0이고 나머지는 항상 자기 자신이기 때문에 값이 달라지지 않는다.

let x = (10 % 100) + (20 % 100); // x = 30
let y = (10 + 20) % 100 // y = 30
x === y

풀이2. tabulation

데이터를 테이블에 정리하면서 bottom-up 방식으로 해결하는 기법

• 시간복잡도 : O(N)

let tiling = function (n) {
  let memo = [0, 1, 2];
  for (let size = 3; size <= n; size++) {
    memo[size] = (memo[size - 2] + memo[size - 1]) % 1000000007;
  }
  return memo[n];
};

풀이3. dynamic with slicing window

필요한 최소한의 데이터만을 활용하는 것을 말합니다.
크기 n의 문제에 대한 해결을 위해 필요한 데이터는 오직 2개뿐이라는 사실을 이용합니다.

• 시간 복잡도: : O(N)

let tiling = function (n) {
  if (n <= 2) return n;
  let first = 1,
    sec = 2;
  for (let size = 3; size <= n; size++) {
    let next = first + sec;
    first = sec;
    sec = next % 1000000007;
  }
  return sec;
};

슬라이딩 윈도우 알고리즘과 비슷한 투포인터 알고리즘 문제