ERD란?
Entity Relationship Diagram.
요구 사항 기반으로 작성하는 릴레이션 간의 관계를 정의한 Diagram으로 데이터베이스의 뼈대 역할.
관계형 구조로 표현 가능한 데이터를 구성하는 데 유용함.
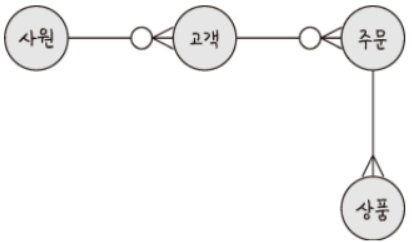
예시)
요구 사항
- 영업사원은 0~n명의 고객을 관리.
- 고객은 0~n개의 주문을 넣을 수 있음
- 주문에는 1~n개의 상품이 들어감
정규화란?
릴레이션 간의 잘못된 종속 관계로 인해 데이터베이스 이상 현상이 발생하여 해결하거나 저장 공간을 효율적으로 사용하기 위해 릴레이션을 분리하는 것.
이상 현상 (Anomaly)
1. 삭제 이상: 튜플 삭제 시 같이 저장된 다른 정보까지 연쇄적으로 삭제
2. 삽입 이상: 튜플 삽입 시 특정 속성 해당하는 값 없어 Null 삽입
3. 수정 이상: 튜플 수정 시 중복 데이터 일부만 삭제되어 데이터 불일치
- 제 1 정규형
릴레이션의 모든 도메인이 더는 분리할 수 없는 원자 값 만으로 구성.
한 개의 기본키에 대해 두 개 이상의 값을 가지는 반복 집합을 분리.
| 번호 | ID | 수강과목 | 성취도 |
|---|---|---|---|
| 1 | 길동 | {C++, Java} | {90%, 10%} |
| 2 | 영식 | {Python, Kotlin} | {30%, 40%} |
수강과목과 성취도 부분에 반복 집합이 존재하여 이를 분리해야 함
| 번호 | ID | 수강과목 | 성취도 |
|---|---|---|---|
| 1 | 길동 | C++ | 90% |
| 1 | 길동 | Java | 10% |
| 2 | 영식 | Python | 30% |
| 2 | 영식 | Kotlin | 40%} |
+) 부분 함수 종속과 완전 함수 종속
부분 함수 종속: {주민번호, 성별}에서, 주민 번호에 따라 사람 이름이 정해지는 상황이면 사람 이름은 {주민번호, 성별}에 부분 함수 종속된다고 한다.
완전 함수 종속: {아이디, 이벤트번호}에서, 둘 모두에 따라 당첨 여부가 정해지는 상황이면 당첨 여부는 {아이디, 이벤트번호}에 완전 함수 종속된다고 한다.
- 제 2 정규형
릴레이션이 제 1 정규형이며 부분 함수 종속성을 제거한 형태(완전 함수 종속).
기본키가 아닌 모든 속성이 기본키에 완전 함수 종속되면 제2 정규형에 속함.
| 번호 | ID | 수강과목 | 성취도 |
|---|---|---|---|
| 1 | 길동 | C++ | 90% |
| 1 | 길동 | Java | 10% |
| 2 | 영식 | Python | 30% |
| 2 | 영식 | Kotlin | 40%} |
제 1 정규형을 만족하는 위 테이블에서 기본 키인 {ID, 수강과목}에 완전 종속되지 못하는 번호 속성이 존재함. (번호는 ID 속성에 종속)
이를 분리하기 위해 테이블을 두 개로 나눔.
| 번호 | ID |
|---|---|
| 1 | 길동 |
| 2 | 영식 |
| ID | 수강과목 | 성취도 |
|---|---|---|
| 길동 | C++ | 90% |
| 길동 | Java | 10% |
| 영식 | Python | 30% |
| 영식 | Kotlin | 40% |
각 테이블은 각 기본 키인 {ID}와 {ID, 수강과목}에 완전 종속되어 제 2 정규형을 만족한다.
단 분해 시에 동등한 릴레이션으로 분리하며 무손실 분해로 진행되어야 한다.
+) 무손실 분해
테이블을 나누고 다시 조인 연산을 통해 합쳤을 경우 데이터 손실이 없는 분해.
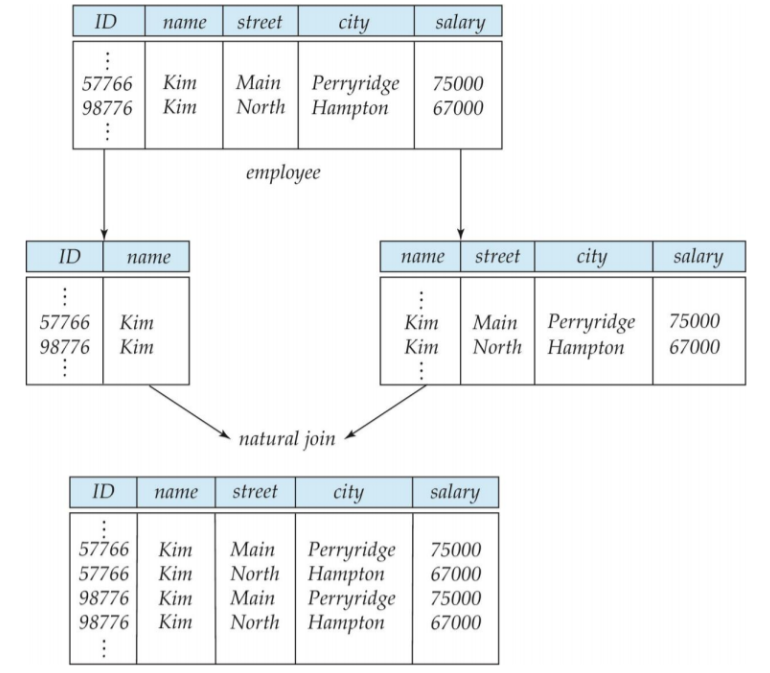
나눈 두 집합 R1, R2의 공통 속성이 R1 또는 R2의 키 인경우 무손실.
위의 경우에는 공통 속성인 name이 키가 아니므로 손실 발생가능.
- 제 3 정규형
제2 정규형이고 기본키가 아닌 모든 속성이 이행적 함수 종속을 만족하지 않는 상태.
+) 이행적 함수 종속
A->B를 만족하고 B->C를 만족할 때 C가 A에 이행적 함수 종속된다라고 함.
| ID | 등급 | 할인율 |
|---|---|---|
| 길동 | 실버 | 10% |
| 문철 | 골드 | 20% |
| 영식 | 다이아 | 40% |
위 테이블은 부분 함수 종속성이 없는 제 2 정규형 테이블이지만, ID -> 등급 을 만족하고 등급 -> 할인율 을 만족하므로 할인율이 ID에 이행적 함수 종속된다.
따라서 위 테이블을 {ID, 등급}과 {등급, 할인율}로 분리하면 제 3 정규형을 만족한다.
- BCNF 정규형 (보이스 / 코드)
제 3 정규형이고 결정자가 후보키가 아닌 함수 종속 관계를 제거한 상태로, 릴레이션의 함수 종속관계에서 모든 결정자가 후보 키인 상태.
| 학번 | 강좌 | 강사 |
|---|---|---|
| 100 | 수학 | 가우스 |
| 100 | 과학 | 뉴턴 |
| 101 | 영어 | 오바마 |
| 101 | 수학 | 가우스 |
| Null | 신강좌 | 새교수 |
위 릴레이션에선 {학번, 강좌} 또는 {학번, 강사}가 후보키가 된다.
하지만 위 테이블에 강좌를 추가하려는 경우, 강좌와 강사를 추가했을 때 학번이 Null이 삽입되는 경우가 발생한다.
후보 키가 아닌 속성이 결정자가 되는 경우 문제가 발생할 수 있으므로 강사 속성으로 테이블을 분리한다.
| 학번 | 강사 |
|---|---|
| 100 | 가우스 |
| 100 | 뉴턴 |
| 101 | 오바마 |
| 101 | 가우스 |
| 강좌 | 강사 |
|---|---|
| 수학 | 가우스 |
| 과학 | 뉴턴 |
| 영어 | 오바마 |
| 신강좌 | 새교수 |
강사 속성이 후보키에 속하도록 테이블을 분리하면 BCNF를 만족하게 된다.
단점
정규형을 이용해 효율적으로 데이터를 관리할 수 있지만 테이블을 나눈다고 무조건 성능이 좋아지는 것이 아님.
조인을 사용해야 하는 쿼리를 처리하는 경우 작은 테이블들 여러개를 합치는 작업을 여러 번 거칠 수 있어 막상 성능은 떨어질 수 있다.
