Minimum Spanning Tree (최소 신장 트리)

먼저, Spanning Tree란?

그래프의 모든 정점이 연결된 순환이 없는 트리 구조이다.

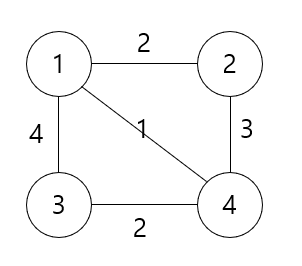
이러한 가중치가 있는 그래프가 있다고 하자.

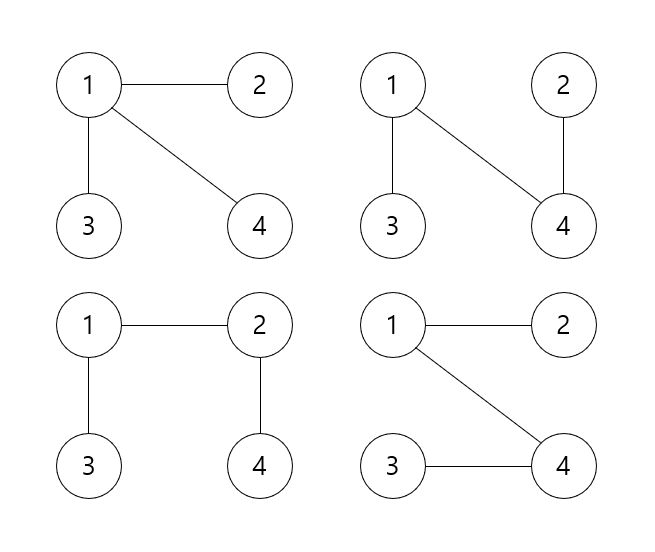
위처럼 그래프에서 순환이 없고 모든 정점들을 거치도록 간선을 선택하여 만들어진 트리라고 예를 들어볼 수 있겠다.

그럼 Minimum Spanning Tree란?

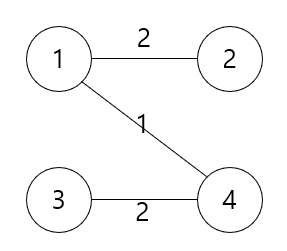
위의 다양한 Spanning Tree들 중 간선의 가중치의 합이 최소인 트리이다

이 Minimum Spanning Tree를 구하는 알고리즘은 두 가지가 있다.

1. Prim Algorithm

   한 정점을 시작점으로 해서, 현재 선택한 정점 그룹과 연결된 정점들 중 가장 가중치가 적은 정점들을 선택하며 트리를 확장하는 알고리즘이다.

   

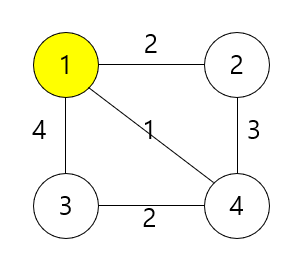
1번 정점을 시작점으로 선택해서 과정을 살펴보자.

1번 정점과 연결된 정점 2, 3, 4 중 가장 가중치가 낮은 정점은 4이다.
따라서 4를 정점 그룹에 추가한다.

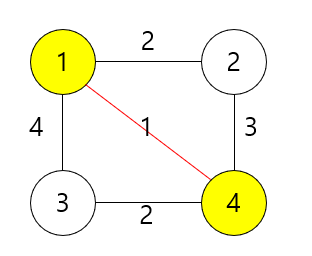
현재 정점 그룹인 (1, 4)와 연결된 정점은 2번과 3번 정점이다.
그룹과 연결된 간선 중 가장 가중치가 낮은 2번(같으면 숫자 낮은 정점 우선) 정점을 그룹에 추가한다.

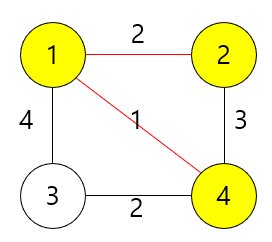
마지막으로 3번 정점을 가중치가 낮은 2짜리 간선을 선택하며 그룹에 추가한다.

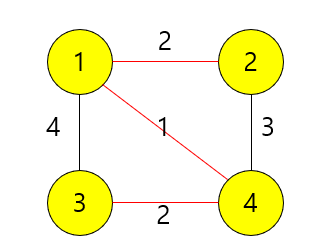
모든 정점을 지나면 Minimum Spanning Tree가 완성된다.

시간 복잡도는 아래와 같다 (정점 V개, 간선 E개라 하면).

1) 모든 정점 V개를 탐색하고 각 정점마다 다른 정점과 연결된 간선(최대 V-1개) 중 최솟값을 Priority Queue를 통해 얻으므로 O($VlogV$) (탐색)

2) 현재 그룹에 해당하는 Priority Queue에 최대 V개의 정점이 삽입될 수 있고 연결된 간선은 최대 E개가 있을 수 있으므로 O($ElogN$)이다.

따라서 시간 복잡도는 O($VlogV+ElogV$)인데 일반적으로 E > V이므로 O($ElogV$)라 할 수 있겠다.

2. Kruskal Algorithm

   간선을 기준으로, 순환이 생기지 않으며 가장 가중치가 적은 간선들부터 순서대로 선택하며 모든 정점이 포함된 하나의 그룹이 만들어지면 종료한다.

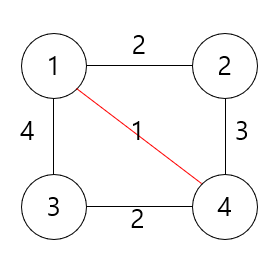
먼저 가장 낮은 가중치를 가진 간선인 1-4 연결 간선을 선택하여 1, 4번 정점을 그룹으로 묶는다.

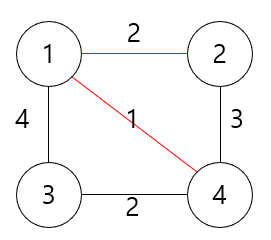
다음으로 낮은 가중치를 가진 간선인 1-2번 간선을 선택하여 2번 정점을 그룹에 추가한다.

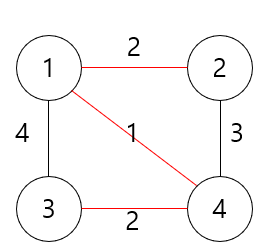
그 다음으로 낮은 가중치를 가진 간선인 3-4번 간선을 선택하여 3번 정점을 그룹에 추가하고, 모든 정점이 그룹에 추가되었으므로 종료한다.

시간 복잡도는 O(1)인 Union-Find 알고리즘을 통해 그룹화하고 그때그때 그룹에 정점이 몇개인지만 체크하면 된다.

따라서 간선을 오름차순으로 정렬하는 O($ElogE$)의 시간복잡도를 가진다.

따라서 Kruskal 알고리즘은 간선 개수가 적을수록 유리하다.