1. 동적 프로그래밍(Dynamic Programming, DP)의 기초
동적 프로그래밍(DP)은 문제를 작은 하위 문제로 나누어 해결하고, 하위 문제의 결과를 재활용하여 전체 문제를 효율적으로 해결하는 기법입니다. DP는 보통 중복 계산을 피하기 위해 하위 문제의 결과를 저장해두고, 필요할 때마다 다시 사용합니다.
• 적용 조건:
-
최적 부분 구조: 원래 문제의 최적 해가 하위 문제의 최적 해로 구성될 수 있어야 합니다.
-
중복되는 부분 문제: 동일한 하위 문제가 여러 번 계산되는 상황이 있어야 합니다.
• DP 구현 방식:
o 메모이제이션 (Memoization): 재귀 호출을 사용하되, 계산한 하위 문제의 결과를 저장하고, 필요할 때 다시 사용합니다. (Top-Down 방식)
o 타뷸레이션 (Tabulation): 작은 문제부터 점진적으로 큰 문제를 해결해 가며, 하위 문제의 결과를 표 형태로 저장합니다. (Bottom-Up 방식)
• 예시: 피보나치 수열 계산
o 단순 재귀로 피보나치 수열을 계산하면 중복된 계산이 많이발생하지만, DP를 사용하면 각 값이 한 번만 계산되어 효율이 크게 향상됩니다.
2. 트라이(Trie)
트라이(Trie)는 문자열이나 키를 효율적으로 저장하고 검색하기 위한 트리 기반 자료구조입니다. 주로 사전(Dictionary) 구현이나 문자열 검색 문제에서 많이 사용됩니다.
• 특징:
o 문자 단위로 노드를 분기하여, 문자열의 접두사(prefix) 단위로 저장됩니다.
o 공통 접두사를 공유하므로, 같은 접두사를 가진 키들을 효율적으로 관리할 수 있습니다.
• 활용 예:
단어 자동완성, 사전 검색, 문자열 검색
o 예를 들어, cat, car, dog라는 단어가 있을 때, c에서 a로 연결된 노드를 통해 cat과 car를 관리할 수 있습니다.
3. AVL 트리 (AVL Tree)
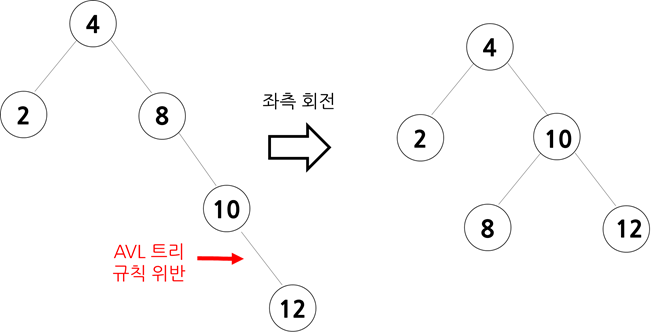
AVL 트리는 균형 이진 탐색 트리의 일종으로, 모든 노드에서 왼쪽과 오른쪽 서브트리의 높이 차이가 최대 1을 유지하도록 설계되었습니다. 이로 인해, AVL 트리는 탐색, 삽입, 삭제 연산에서 균형이 유지되어 빠른 속도를 보장합니다.
• 특징:
o 삽입이나 삭제 후 균형이 깨질 경우, 트리를 회전(Rotation)하여 높이를 조정합니다.
o 각 노드에서 왼쪽과 오른쪽 서브트리의 높이 차이가 1을 넘지 않도록 유지합니다.
• 활용 예:
검색 기능이 중요한 애플리케이션에서, 균형을 유지하면서 데이터 삽입/삭제가 빈번한 경우에 유용합니다.
4. 레드-블랙 트리 (Red-Black Tree)
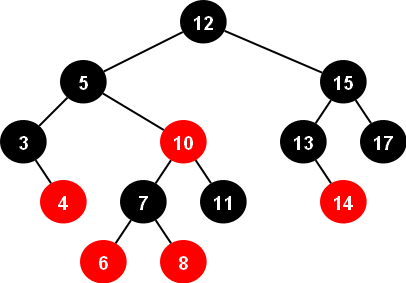
레드-블랙 트리는 균형을 유지하는 또 다른 이진 탐색 트리로, AVL 트리와 비슷하지만 다소 다른 규칙을 따릅니다. 자체적인 색상 규칙을 통해 균형을 유지하며, 삽입 및 삭제 연산 시 최대 O(log n)의 시간 복잡도를 보장합니다
• 특징:
o 각 노드에 색상(빨간색 또는 검은색)을 부여하여, 삽입과 삭제 시 균형을 조정합니다.
o 루트 노드와 리프 노드는 항상 검은색이어야 하며, 빨간색 노드의 자식 노드는 항상 검은색이어야 하는 등 특정 규칙을 지킵니다.
o 레드-블랙 트리는 AVL 트리보다 다소 덜 엄격하게 균형을 유지하므로, 삽입과 삭제가 빈번한 경우에 더 효율적일 수 있습니다.
• 활용 예:
자바의 TreeMap이나 TreeSet 같은 내부 구현에서 레드-블랙 트리를 사용합니다.
• 시간복잡도
레드-블랙 트리의 삭제 연산의 시간복잡도는 O(log n)
: 레드-블랙 트리가 항상 균형을 유지하기 때문에 높이가 최대 log(n)을 넘지 않기 때문입니다. 삭제 과정에서 색상 변경과 회전은 최대 O(log n) 번 수행되므로, 전체 삭제 연산의 시간복잡도는 O(log n)입니다.
Referance
https://velog.io/@nnoshel/AVL-%ED%8A%B8%EB%A6%AC
https://hongcoding.tistory.com/178
