트리의 기본 개념 및 용어
계층적 구조를 가진 형태의 그래프
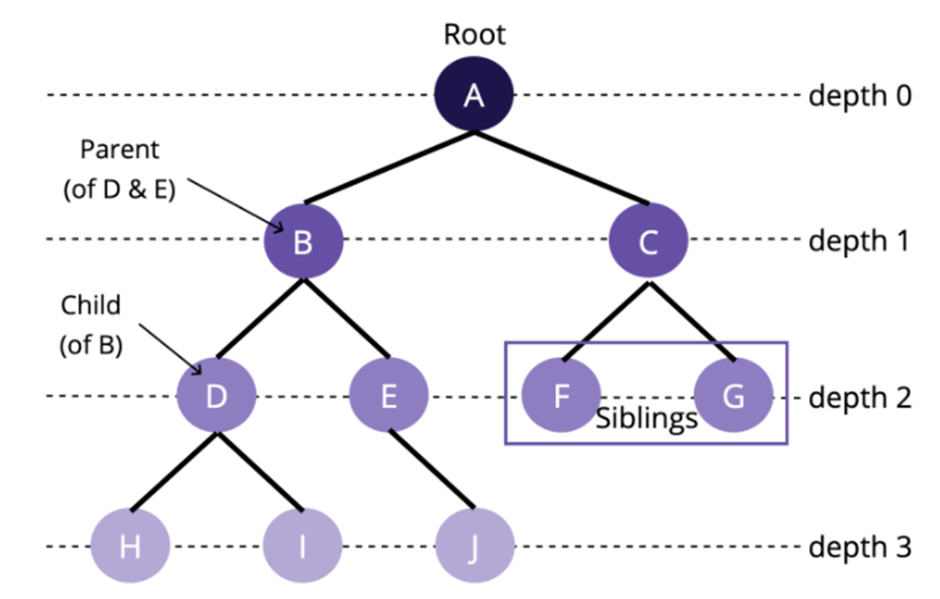
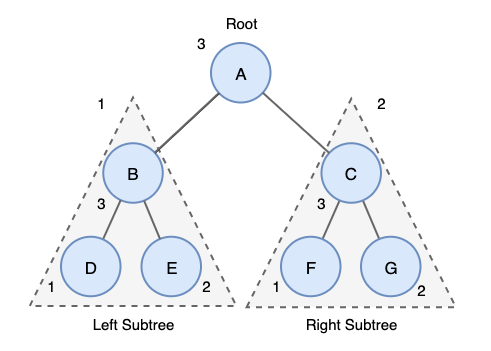
1. 루트 (Root):
o 트리의 최상위 노드입니다. 트리는 하나의 루트 노드를 가지며, 모든 노드는 루트에서 시작하여 내려가는 구조를 가집니다.
2. 노드 (Node):
o 트리의 구성 요소로, 각각의 노드에는 데이터가 저장됩니다.
o 각 노드는 부모 노드와 자식 노드를 가질 수 있으며, 트리의 계층을 이루는 기본 단위입니다.
3. 리프 (Leaf):
o 자식 노드가 없는 노드를 리프 노드라고 합니다. 트리의 가장 말단에 위치하며, 더 이상 분기가 없는 노드입니다.
4. 부모와 자식 관계:
o 부모 노드는 자식 노드를 가지며, 부모-자식 관계를 통해 트리의 계층 구조가 형성됩니다.
o 예를 들어, A가 B와 C의 부모라면 B와 C는 A의 자식입니다.
이진 트리 (Binary Tree)
이진 트리는 각 노드가 최대 두 개의 자식 노드만을 가지는 트리 구조입니다.
이진 트리는 간단하면서도 다양한 문제를 해결하기에 유용한 구조입니다.
• 특징:
o 각 노드가 왼쪽 자식과 오른쪽 자식을 최대 하나씩 가질 수 있습니다.
o 트리의 높이가 낮을수록 탐색 속도가 빠릅니다.
활용 예: 이진 트리는 데이터를 계층적으로 관리하거나, 특정 값 검색 및 정렬 등에 유용하게 사용됩니다.
이진 탐색 트리 (Binary Search Tree, BST)
이진 탐색 트리는 이진 트리의 한 종류로, 왼쪽 자식은 부모보다 작은 값, 오른쪽 자식은 부모보다 큰 값을 가지는 구조입니다. 이러한 규칙 덕분에 데이터 검색이 빠르게 이루어질 수 있습니다.
• 특징:
o 탐색 효율성: 트리의 균형이 잘 잡힌 경우, 특정 값에 대한 검색, 삽입, 삭제 작업이 평균 O(log n) 시간 복잡도를 가집니다.
o 정렬된 데이터 관리: 데이터가 정렬된 상태로 유지되므로, 정렬된 데이터를 빠르게 관리하고 검색할 수 있습니다.
활용 예: 숫자나 알파벳을 정렬된 형태로 관리할 때 유용하며, 주로 검색 기능이 중요한 애플리케이션에서 자주 사용됩니다.
트리의 순회 방법
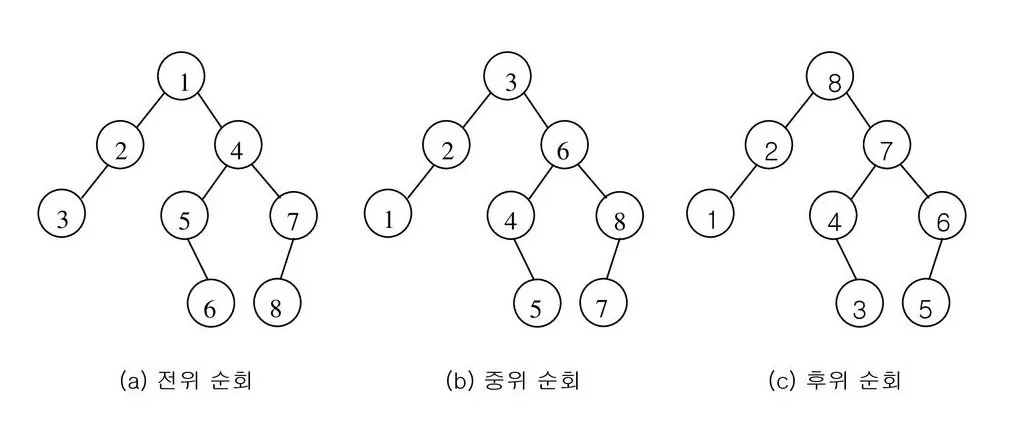
트리 순회는 트리의 모든 노드를 한 번씩 방문하는 과정입니다. 순회 방법에 따라 방문 순서가 달라지며, 각 순회 방식은 특정 문제를 해결하는 데 유용합니다.
1. 전위 순회 (Pre-order Traversal):
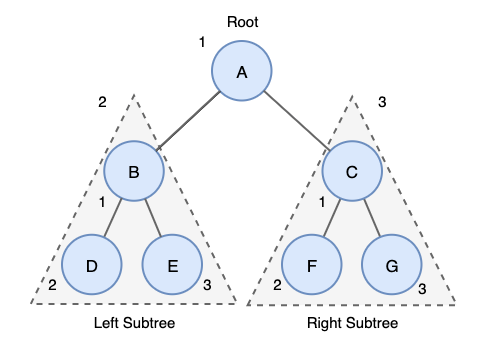
o 순서: 루트 → 왼쪽 자식 → 오른쪽 자식
o 특징: 루트를 먼저 방문하므로, 트리의 구조를 직관적으로 이해할 때 유용합니다.
2. 중위 순회 (In-order Traversal):
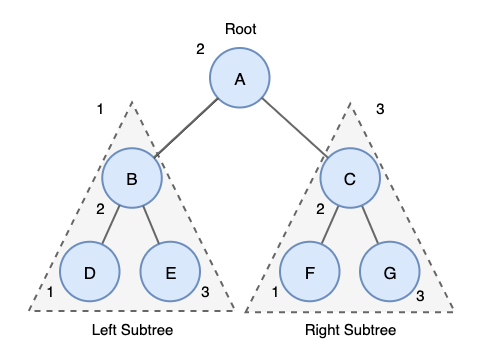
o 순서: 왼쪽 자식 → 루트 → 오른쪽 자식
o 특징: 이진 탐색 트리에서 중위 순회를 사용하면 노드가 정렬된 순서로 방문됩니다.
3. 후위 순회 (Post-order Traversal):
o 순서: 왼쪽 자식 → 오른쪽 자식 → 루트
o 특징: 리프 노드를 먼저 방문하고 루트를 나중에 방문하므로, 하위 작업을 모두 처리한 후 최종 결과를 계산할 때 유용합니다.
그래프의 기본 개념 및 용어
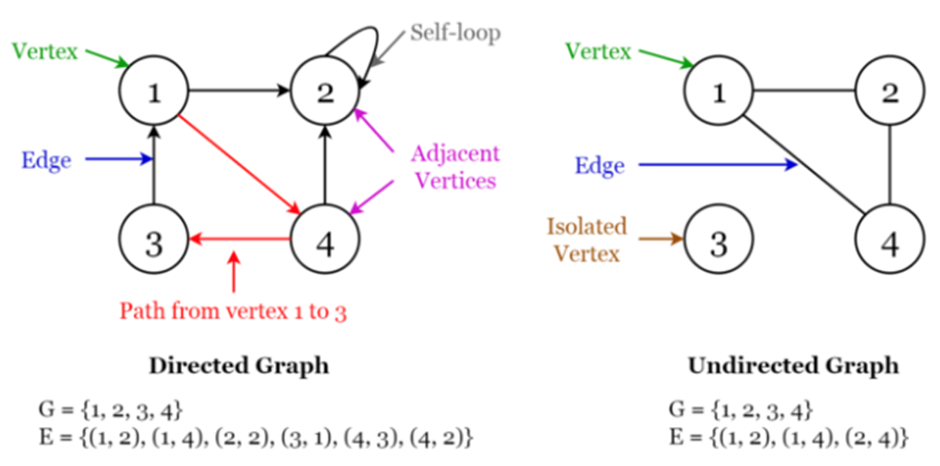
1. 정점 (Vertex, Node):
o 그래프에서 데이터를 담고 있는 요소를 말합니다. 예를 들어, 도시 지도에서는 도시가 정점이 될 수 있습니다.
2. 간선 (Edge):
o 두 정점을 연결하는 선으로, 두 정점 사이의 관계를 나타냅니다. 예를 들어, 도시 지도에서는 도시를 연결하는 길이 간선이 됩니다.
o 방향성:
1. 무방향 그래프: 간선에 방향이 없으며, 연결된 두 정점이 서로 상호작용할 수 있습니다.
2. 유방향 그래프: 간선에 방향이 있어, 한쪽 방향으로만 연결된 구조입니다.
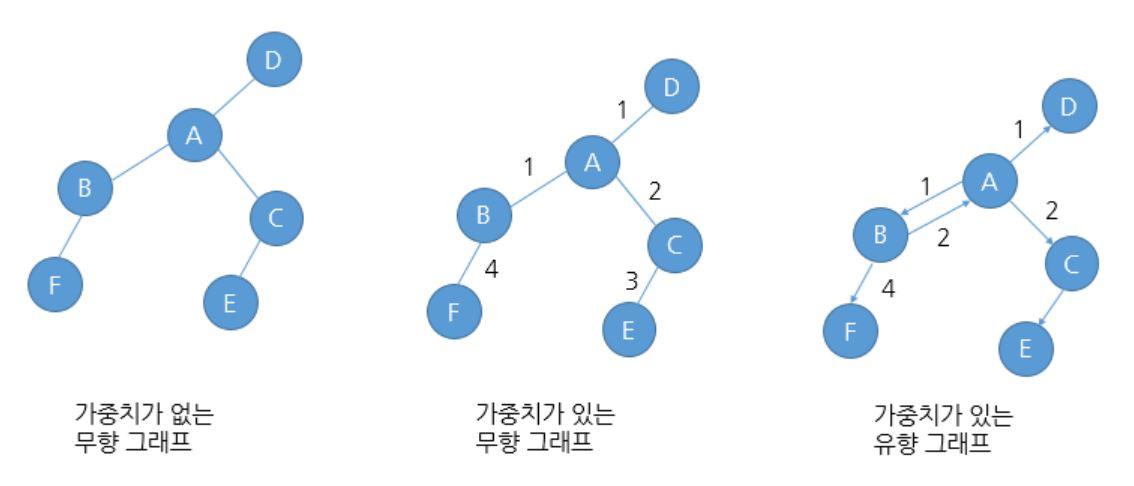
o 가중치 (Weight):
간선에 가중치가 부여되면, 이를 가중치 그래프라고 합니다. 예를 들어, 두 도시 사이의 거리나 비용이 가중치로 표현될 수 있습니다.
그래프의 표현 방식
그래프는 정점과 간선의 연결 관계를 표현하기 위해 인접 리스트와 인접 행렬을 주로 사용합니다.
1. 인접 리스트 (Adjacency List):
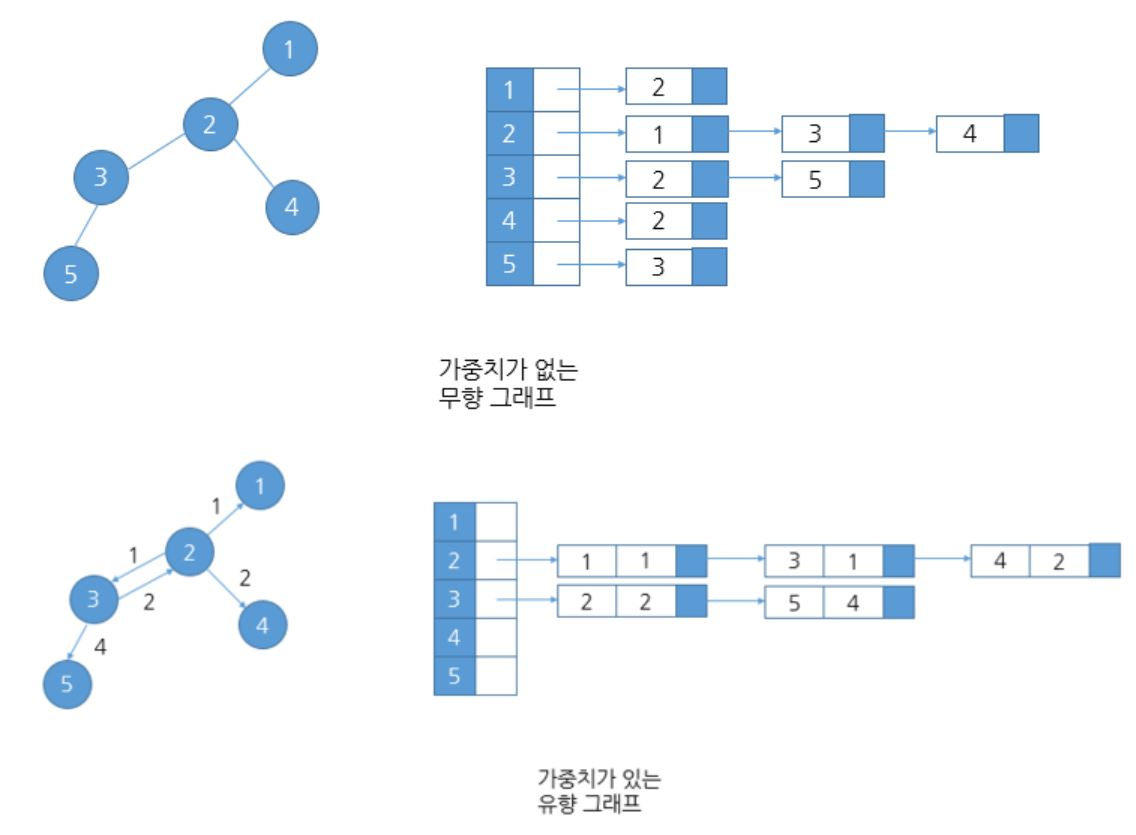
o 각 정점이 자신과 연결된 정점들을 리스트 형태로 저장하는 방식입니다.
o 효율성: 간선이 적은 희소 그래프(Sparse Graph)에 적합하며, 메모리를 절약할 수 있습니다.
2. 인접 행렬 (Adjacency Matrix):
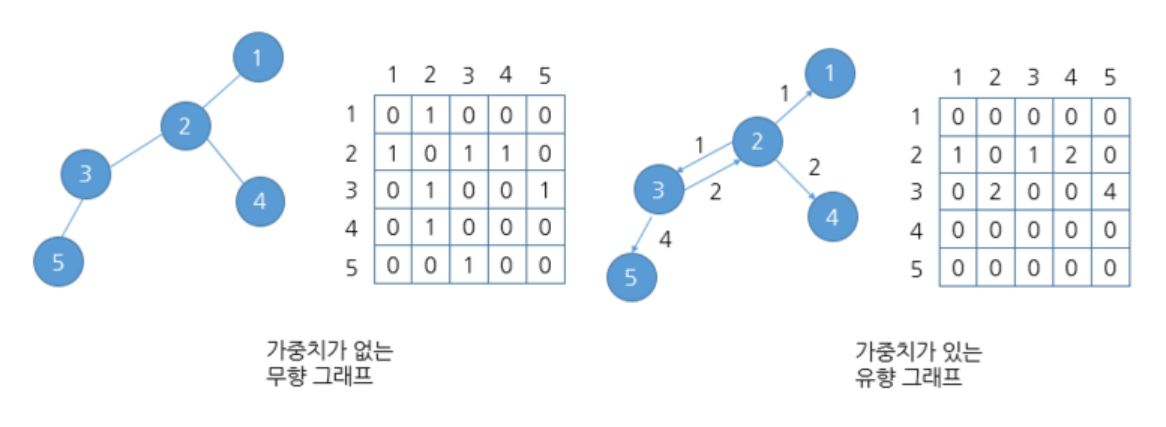
o 정점 간의 연결 관계를 2차원 배열(행렬)로 표현하는 방식입니다.
o 효율성: 간선이 많은 밀집 그래프(Dense Graph)에 적합하며, 특정 두 정점이 연결되어 있는지 확인할 때 빠릅니다.
그래프 탐색 방법
그래프 탐색은 모든 정점을 방문하거나 특정 조건에 맞는 정점을 찾는 방법으로, 대표적으로 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS)이 있습니다.
1. 깊이 우선 탐색 (Depth-First Search, DFS):
o 정점의 가장 깊은 곳까지 탐색한 후, 다시 돌아와 다음 정점을 탐색하는 방식입니다.
o 구현 방법: 스택(또는 재귀 호출)을 사용하여 현재 정점에서 갈 수 있는 한 끝까지 탐색합니다.
o 특징: 경로 탐색이나 백트래킹이 필요한 문제에 자주 사용됩니다.
o 예시: 미로 찾기에서 한 경로로 끝까지 이동한 후, 막히면 돌아와서 다른 경로를 탐색하는 경우.
2. 너비 우선 탐색 (Breadth-First Search, BFS):
o 시작 정점에서 가까운 정점부터 넓게 탐색하는 방식입니다.
o 구현 방법: 큐를 사용하여 현재 정점에서 연결된 모든 정점을 탐색한 후, 다음 깊이의 정점을 순차적으로 탐색합니다.
o 특징: 최단 경로 찾기(가중치가 동일한 경우)에 적합합니다.
o 예시: 두 정점 사이의 최단 거리를 찾는 경우.
트리와 그래프의 차이점
• 구조:
o 트리(Tree)는 사이클(순환)이 없는 그래프의 특별한 형태로, 부모-자식 관계가 명확합니다.
o 그래프(Graph)는 사이클이 존재할 수 있으며, 방향성이 있거나 없을 수 있습니다. 정점 간의 관계가 보다 자유롭습니다.
• 연결성:
o 트리는 하나의 루트 노드에서 시작하여 모든 노드가 연결됩니다.
o 그래프는 여러 개의 연결된 구성 요소를 가질 수 있으며, 루트 노드가 필요 없습니다.
• 용도:
o 트리는 계층적인 구조나 종속 관계를 나타낼 때 주로 사용됩니다.
o 그래프는 정점 간의 복잡한 연결 관계를 나타내는 데 주로 사용되며, 소셜 네트워크, 지도, 네트워크 연결 등 다양한 분야에 활용됩니다.
https://bnzn2426.tistory.com/115
https://velog.io/@yeonkr/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%ED%8A%B8%EB%A6%AC-%EC%88%9C%ED%9A%8CTree-Traversal
