문제 이해
공격수가 먼저 공격하고 수비수는 이후에 수비를 한다.
공격수는 격자에 놓인 도미노를 동, 서, 남, 북 중 원하는 방향으로 넘어뜨린다.
이 때 길이가 K인 도미노가 특정 방향으로 넘어질 때, 자기 자신을 포함한 K개의 도미노(즉, 방향으로 K-1개의 도미노)가 쓰러진다.
이 때, 도미노의 특성 상 연쇄적으로 도미노가 넘어질 수 있으며, 이 때는 넘어진 도미노의 길이만큼 진행되는 방향으로 도미노가 추가적으로 넘어질 수 있다.
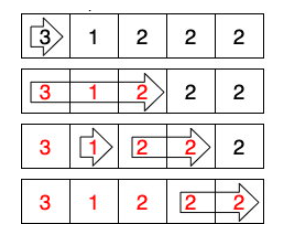
- 3을 넘어뜨리니 3,1,2가 넘어진다. 이 때 1은 오른쪽 0개를 넘어뜨리고 2는 오른쪽 1개를 넘어뜨린다. 따라서 2 오른쪽의 2도 넘어지게 되고, 오른쪽의 2도 그 오른쪽 도미노를 넘어뜨리므로 결국 1줄이 모두 넘어지는 것이다
수비수는 넘어진 도미노 중 하나를 세울 수 있는데, 넘어지지 않은 도미노를 세우면 아무 일도 일어나지 않는다(즉, 수비턴을 버린다)
공격수가 각 라운드에 넘어뜨린 도미노의 개수의 총합이 공격수의 점수가 된다.
공격수와 수비수의 행동 기록이 주어질 때 공격수의 점수와 게임판 최종 상태를 출력하는 문제이다.
문제 풀이
사실 복잡한 알고리즘보다는 Brute-force와 가까운 문제였던 것 같다.
단지, 오른쪽으로 넘어뜨리면서 앞으로 남을 넘어뜨릴 도미노 개수와 현재 넘어뜨린 도미노의 높이를 비교하여 더 큰 값으로 갱신하는 알고리즘이 추가되는 것 뿐이였다.
예를 들어 위에서 3, 1, 2, 2, 2가 넘어가는 과정을 보자.
3은 자기 자신을 넘어뜨렸으니 오른쪽 도미노로 갔을 때 (3-1, 1)이 비교되어야 한다.
이 중 큰 값을 저장해야하므로 2가 저장될 것이다.
이후 2를 넘어뜨릴 때 (2-1, 2)가 비교되고, 이 중 큰 값을 골라야 한다.
따라서 이 중 큰 값인 2가 저장될 것이다.
다음 2를 넘어뜨릴 때는 위에서 선택된 2를 활용하여 (2-1, 2)가 비교될 것이고, 이 중 큰 값인 2가 저장될 것이다. 그 다음 2도 똑같은 과정을 거치면 될 것이다.
코드
import java.io.*;
import java.util.*;
public class Main {
static StringBuilder sb = new StringBuilder();
static int N, M, R;
static int[][] arr;
static char[][] dominos;
public static void main(String[] args) {
FastReader sc = new FastReader();
N = sc.nextInt();
M = sc.nextInt();
R = sc.nextInt();
arr = new int[N+1][M+1];
// Domino의 높이가 저장된 배열
dominos = new char[N+1][M+1];
// Domino의 상태가 저장된 배열
for(int i=1;i<=N;i++) {
for(int j = 1;j<=M;j++) {
arr[i][j] = sc.nextInt();
if(arr[i][j]==0) {
dominos[i][j] = 'F';
}
else {
dominos[i][j] = 'S';
}
}
}
int ans = 0;
for(int r =0;r<R;r++) {
int s_x = sc.nextInt();
int s_y = sc.nextInt();
char s_dir = sc.next().charAt(0);
int want_x = sc.nextInt();
int want_y = sc.nextInt();
ans += domino(s_dir, s_x, s_y, want_x, want_y);
// (s_x, s_y)부터 s_dir 방향으로 무너뜨린다
// 또한 수비수 측이 (want_x, want_y) 도미노를 세운다
// 반환된 값을 모두 더한 것이 공격수의 점수가 될 것이다
}
sb.append(ans+"\n");
for(int i=1;i<=N;i++) {
for(int j = 1;j<=M;j++) {
sb.append(dominos[i][j]+" ");
}
sb.append("\n");
}
System.out.println(sb);
}
static int domino(char s_dir, int s_x, int s_y,
int want_x, int want_y) {
// (s_x, s_y)부터 s_dir 방향으로 무너뜨린다
// 또한 수비수 측이 (want_x, want_y) 도미노를 세운다
// 또한 이 때 넘어뜨린 도미노 개수를 반환한다.
if(dominos[s_x][s_y]=='F') {
// 도미노가 이미 넘어져 있는 상황이므로 공격에선 아무런 상황이 발생하지
// 않는다. 따라서 0을 반환하고 수비만 수행한다
dominos[want_x][want_y] = 'S';
return 0;
}
int sum = 0;
int go = 0;
int max = arr[s_x][s_y];
// 방향에 따라 배열의 이동 방향만 바뀔 뿐 알고리즘은 똑같다
// 따라서 E에서만 설명하고, 남은 방향은 알고리즘만 적용하면 된다
if(s_dir=='E') {
while(max>0 && s_y+go<=M) {
if(dominos[s_x][s_y+go]!='F') {
// 도미노가 넘어져 있는 상황이 아니다.
// 즉, 도미노를 넘어뜨려야 한다.
// 먼저 도미노가 넘어졌으므로 넘어뜨린 도미노 개수인 sum에
// 1을 더하고, 해당 도미노를 넘어뜨린다(F로 변환)
// 이후, 이전에 존재하던 "넘어뜨릴 수 있는 도미노 개수"와
// 현재 도미노 높이를 비교하여 큰 값을
// 다음 과정부터 넘어뜨릴 수 있는 도미노 개수로 설정해주면 된다
dominos[s_x][s_y+go] = 'F';
max = Math.max(arr[s_x][s_y+go], max);
sum++;
}
max = max - 1;
// 현재 도미노를 넘어뜨렸으므로 앞으로 max-1만큼의 도미노를
// 더 넘어뜨릴 수 있는 것이다.
go = go + 1;
// 방향을 한 칸 이동한다
}
}
else if(s_dir=='W') {
while(max>0 && s_y-go>0) {
if(dominos[s_x][s_y-go]!='F') {
dominos[s_x][s_y-go] = 'F';
max = Math.max(arr[s_x][s_y-go], max);
sum++;
}
max = max - 1;
go = go + 1;
}
}
else if(s_dir=='N') {
while(max>0 && s_x-go>0) {
if(dominos[s_x-go][s_y]!='F') {
dominos[s_x-go][s_y] = 'F';
max = Math.max(arr[s_x-go][s_y], max);
sum++;
}
max = max - 1;
go = go + 1;
}
}
else {
while(max>0 && s_x+go<=N) {
if(dominos[s_x+go][s_y]!='F') {
dominos[s_x+go][s_y] = 'F';
max = Math.max(arr[s_x+go][s_y], max);
sum++;
}
max = max - 1;
go = go + 1;
}
}
dominos[want_x][want_y] = 'S';
return sum;
}
static class FastReader // 빠른 입력을 위한 클래스
}결과

- 부분 맞았습니다 이유 : 이미 넘어뜨린 도미노를 공격할 경우 아무런 상황이 발생하지 않아야 한다. 하지만 이 부분을 고려하지 않았기 때문에 AC가 나오지 않았다.
