문제 이해

십자모양의 카드에 모서리마다 1 ~ 9 중 하나의 숫자가 쓰여 있다
쓰여진 숫자를 시계 방향으로 읽어서 만들 수 있는 수가 4개 존재한다.

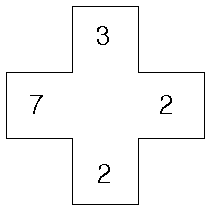
위 사진에서 3을 시작으로 보면 3227을 만들 수 있으며, 2를 시작으로보면 2273, 2732를 만들 수 있고, 7을 시작으로 보면 7322를 만들 수 있을 것이다.

이렇게 만들 수 있는 숫자 중 최소값을 시계수라고 한다.
(위 예시에서는 2273이 가장 작으므로 2273이 시계수이다)

시계 방향 순으로 숫자 4개가 입력될 것이다.
이 숫자로 만들 수 있는 시계수보다 작은 모든 시계수들을 구하는 것이 문제이다.

---

문제 풀이

1121을 예시로 보자.
우리가 1121 십자 카드로 만들 수 있는 수는 1121, 1211, 2111, 1112가 될 것이다.

나는 이 수를 보고 가장 오른쪽에 있는 수(가장 낮은 자릿수)를 가장 왼쪽에 붙이면 다음 십자 카드로 만들 수 있는 수를 만들 수 있다는 것을 알게 되었다.

(ex) 1234일 경우, 4를 왼쪽에 붙여 4123을 만들 수 있고, 4123에서 3을 다시 왼쪽에 붙여 3412를 만들 수 있고, 2341 또한 만들 수 있을 것이다.

1111이 최소 4자리 시계수 이기 때문에, 1111부터 주어진 숫자로 만들 수 있는 시계수 사이에 존재하는 모든 4자리 숫자에 대하여 시계수인지를 판단하여 개수를 세는 방식을 활용하였다.

---

코드

import java.io.*;
import java.util.*;

public class Main {
	static StringBuilder sb = new StringBuilder();
	static int size;
	static String answer_str;
	static String reverse_answer_str;
	
	static boolean check(int t) {
		int tmp = t;
		for(int i =0;i<3;i++) {
			if(tmp%10==0) return false;
            // 시계수는 0이 존재할 수 없으므로 False 반환
			
			tmp = tmp /  10 + 1000 * (tmp%10);
			// 가장 큰 자릿수를 가장 오른쪽에 붙이는 과정
            // tmp / 10 : 1 ~ 3번째 자릿수를 한칸씩 오른쪽으로 땡김
            // 1000 * (tmp%10) : 가장 낮은 자릿수를 가장 왼쪽에 붙임
			if(tmp < t) return false;
            // tmp < t라면 t로 만들 수 있는 더 작은 수가 존재한다는 의미이므로
            // t(Input 값)은 시계수가 아니다. 따라서 False 반환
		}
		
		return true;
	}
	
	public static void main(String[] args) {
		FastReader sc = new FastReader();

		int num = 1000 * sc.nextInt() + 100 * sc.nextInt() 
                                 + 10 * sc.nextInt() + sc.nextInt();

		int tmp = num;
		for(int i =0;i<3;i++) {
			tmp = tmp / 10 + 1000*(tmp%10);
			num = Math.min(num, tmp);
		}
		
		int ans = 0;
		for(int t = 1111;t<num;t++) {
			if(check(t)) ans++;
            // check(t) = true라면 t는 시계수. 따라서 ans에 1을 더해준다.
		}
		
		System.out.println(ans+1);
        // 앞에 9개의 숫자가 있으면 ans = 9이다.
        // 즉, 우리가 구하고 싶은 num은 10번째 시계수이기 때문에 ans+1을 출력한다.
	}

	static class FastReader // 빠른 입력을 위한 클래스
}

---

결과

• 3번째 틀렸습니다 : 디버그 할 떄 활용했던 출력문구를 삭제하지 않고 제출해서 발생했다.