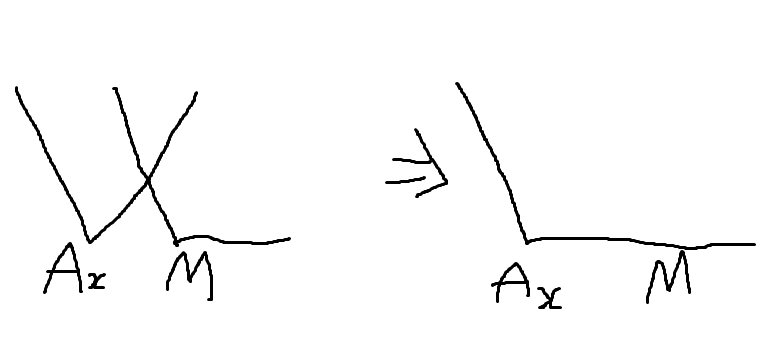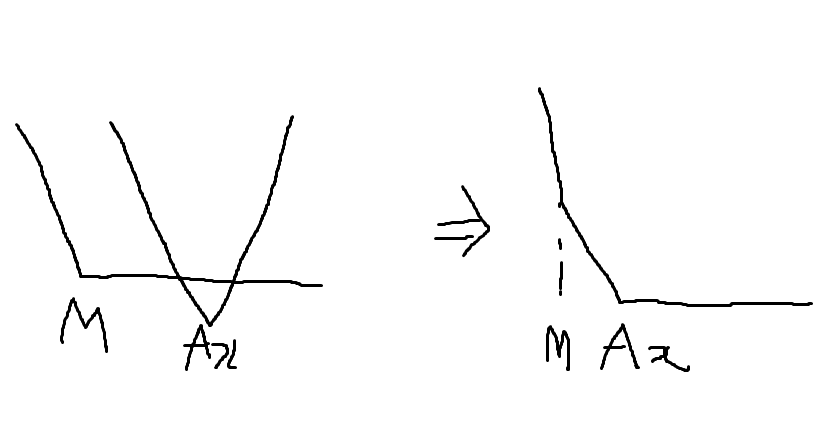Slope Trick

Slope Trick

백준 문제를 풀다가 처음 접하게된 용어로
관련 문제를 푸는 것도 너무 어려웠고 이 개념을 이해하는 과정도 꽤 힘들었다.

https://www.acmicpc.net/problem/13323

이 문제와 관련되어 있으니 먼저 풀어보실 분은 풀어봐도 된다.

관련 문제

https://codeforces.com/contest/713/problem/C
https://codeforces.com/contest/866/problem/D
https://github.com/ranaldmiao/sg_noi_archive/blob/master/2018/statements/NOI%202018%20Tasks.pdf

전부 수열과 관련된 문제들인데 백준 13323번이나 코드 포스 C번은 사실상 같은 문제다.
13323번은 A수열 안에 숫자가 무작위로 존재하고 B수열은 오름차순 순열인데 2개의 차이를 가장 작게 하는 B수열을 구하는 것이다.
즉, A수열 안의 각각 숫자를 1씩 증가, 혹은 감소시켜서 B수열을 만드는 최소 숫자 증감 횟수를 구하는 것과 같은 말로 C번과 같은 문제라고 봐도 된다.

어쨋든, A수열을 어떻게든 최소로 오름차순을 만들어야하는데 어떻게 접근해야할까?

접근

13323번의 예제1 입력을 예시로 사용하겠다.
A수열이 (9 4 8 20 14 15 18)라고 가정하자.
앞으로 $An$ = (A수열의 n번째 자리의 숫자)로 활용하겠다.
그리고 $F(x,k)$라는 함수를 만들어 사용하겠다.

x=1인 경우

ex) $F(1,2)$라는 것은 A수열의 1번째 자리수가 2가 되기 위한 최소 숫자 증감 횟수이다.
그렇다면 A수열의 첫번째 숫자는 9이므로 최소 7번 움직여야 한다.

즉, $F(1,k)$라는 것은 $|k-A1|$

x>=2인 경우

$F(x,k)$이라는 것은 A수열의 x번째 자리수가 k가 되야할 때
A수열 x번째자리까지 오름차순이 되기 위해서 전체적으로 증감해야하는 최소 숫자 개수이다.
그렇기에 $F(x,k) = min(F(x-1,k-1),...F(x-1,0)) + |k-Ax|$
min 수식 부분에서 k-1까지의 숫자만 존재하고 그 이상은 없는 이유는
A수열이 결국 오름차순이 되려면 아래 자리 숫자들이 k보다 작아야하기 때문이다.

ex) $F(2,3)$은 결국 $min(F(1,2),F(1,1),F(1,0)) + |3-4|$가 된다.

만약 x부분을 상수로 정해두고 $|k-Ax|$ 그래프를 그린다면 모두가 잘 아는 절대값 그래프가 나온다.

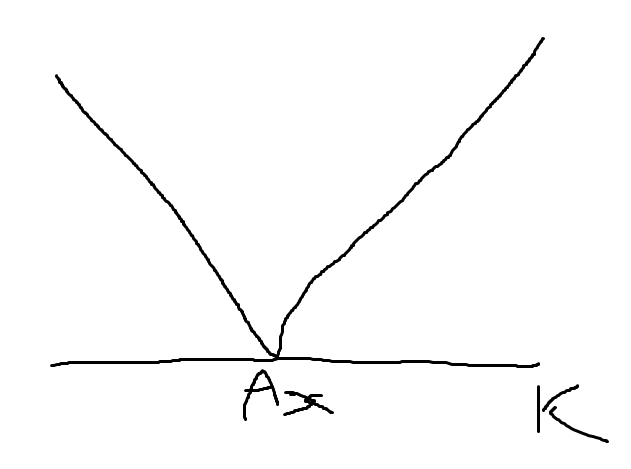
그렇다면 $min(F(x-1,k-1),...F(x-1,0))$를 그래프로 그릴 수만 있다면
어떻게든 최소 값을 찾을 수 있을 것이다.

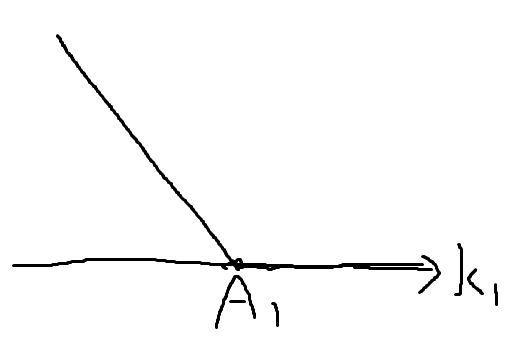
먼저 $x-1=1$인 경우의 $F(x-1,k1)$ 그래프를 그려보면 아래와 같다.
그 중 최소값인 $k1$은 $A1$이다.

그렇다면 $F(2,k) = min(F(1,k-1),...F(1,0)) + |k-A2|$는?

$F(1,9)$는 일단 예시1)에 따라 최솟 값인 0이다.
이 때, $k=9$가 된다면 $min(F(1,k-1),...F(1,0)) = F(1,8) = 1$이 된다.
$k=10$이라면 $min(F(1,k-1),...F(1,0)) = F(1,9) = 0$이 된다.

즉, $min(F(1,k-1),...F(1,0))$는 $F(1,k)$를 k축으로 1씩 평행이동하여 그래프로 나타낼 수 있는 것이다.

$F(2,k) = min(F(1,k-1),...F(1,0)) + |k-A2|$(예시에 따라, A2=4)
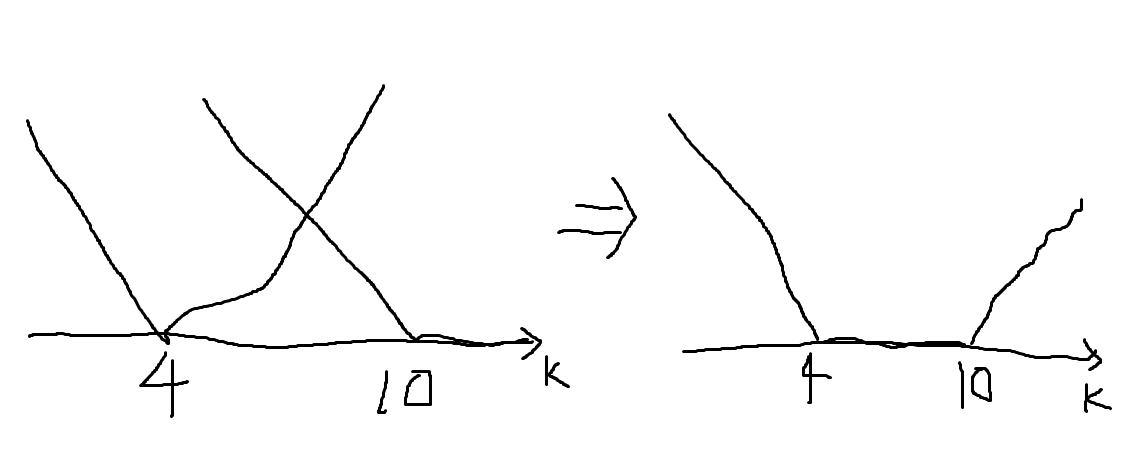
는 아래와 같이 2개의 그래프의 합으로 나타낼 수 있다.

사실상 그래프에서 기울기가 증가하는 부분에서는 최솟값이 나타나지 않기에
아예 0으로 만들어버려도 무방하다.

$F(x-1,k)$를 k축으로 1씩 평행이동한 그래프의 최솟 값이 M이라고 하면
$|k-Ax|$를 더해줄 시 3가지 경우로 상태를 나누어볼 수 있다.

1. $Ax<M$일 경우(Ax와 M 사이가 기울기가 0이될 때)
   
   그래프 전체의 최솟 값이 Ax와 M의 차이만큼 오르게되고
   k가 Ax일 때나 M일 때나 최솟 값을 가진다.

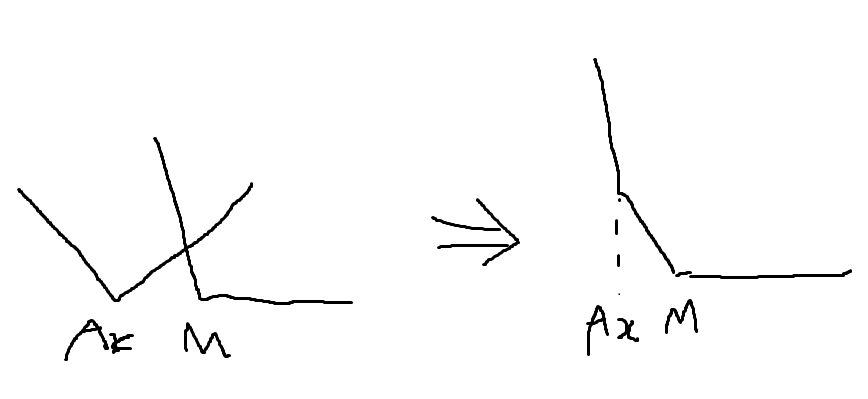
2. $Ax<M$일 경우(Ax와 M 사이가 기울기가 -가될 때)
   
   그래프 전체의 최솟 값이 Ax와 M의 차이만큼 오르게되고
   k가 M일 때만 최솟 값을 가진다.

3. $Ax>=M$일 경우
   
   그래프 전체의 최솟 값이 그대로이며
   k가 Ax일 때만 최솟 값을 가진다.

결국, 우선순위 큐를 활용하여 새로 들어온 숫자 $Ai$가
전에 들어왔던 숫자들보다 높거나 같으면 push만 적용하면 될 것이고

새로 들어온 숫자 $Ai$가
전에 들어왔던 숫자들보다 낮으면 제일 높은 숫자를 pop시키고
$Ai$를 push하면 되는 것이다.

결국, 우선 순위 큐 안에는 같은 숫자들이 여러 개 존재할 수도 있다.
만약에 큐 안에 (20,20)이 존재한다면
k=20을 기준으로 왼쪽은 기울기가 -2, 오른쪽은 기울기가 0이라는 뜻이다.

큐 안에 (4,20,20)이 존재한다면
k<4인 구역은 기울기가 -3
4<k<20인 구역은 기울기가 -2
k>20인 구역은 기울기가 0이다.