구간 합 - 이.코.테

📖 구간 합?

합 배열을 이용하여 연산의 횟수를 줄이는 것이 목적인 알고리즘입니다.

합배열

기존의 배열을 전처리한 배열이며 이를 활용하여 구간 합을 더 빠른 속도로 계산하기 위한 목적을 가지고 있습니다.

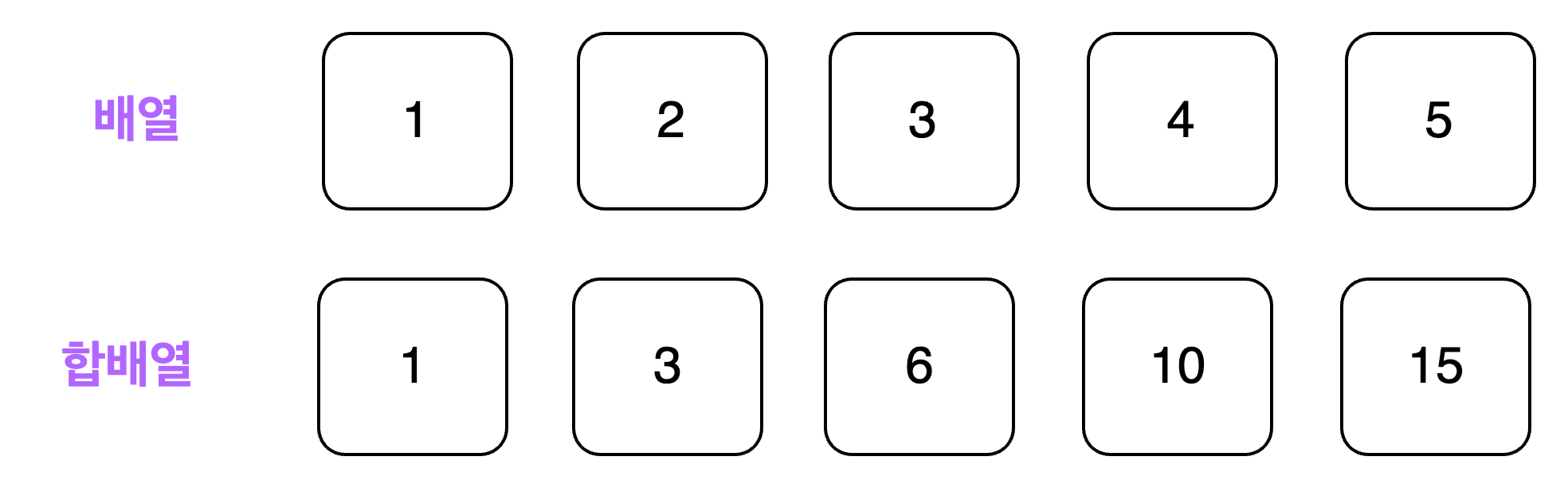
기존의 배열을 A, 합배열을 B라고 한다면 B[i] = B[i-1] + A[i] 라는 공식이 나옵니다.

구간합의 경우도 i부터 j까지 구간 합을 구한다면 S[j] - S[i-1]라는 공식이 나옵니다.

기존 배열로만 합을 구한다면 시간복잡도는 O(N)이지만 합배열을 미리 구현해놓으면 O(1)로 감소합니다. 기존 배열의 일정 범위의 합을 구하는 과정이 줄어 시간 복잡도가 감소하게 됩니다.

😮 사용되는 사례

구간 합 구하기2

BOJ 11660

해당 문제는 2차원배열을 입력받고 (x1,y1)부터 (x2,y2)까지 구간 합을 구하는 문제입니다. 제한시간은 1초입니다. 범위는 1..N..1024 , 1..M..100_000 입니다. 1초에 약 1억번을 연산하는데 최대 연산 회수가 1억번이 넘기 때문에 반복문으로 푸는 것은 시간초과 됩니다. 2차원 배열의 합배열을 먼저 구하여 문제를 풀어야합니다.

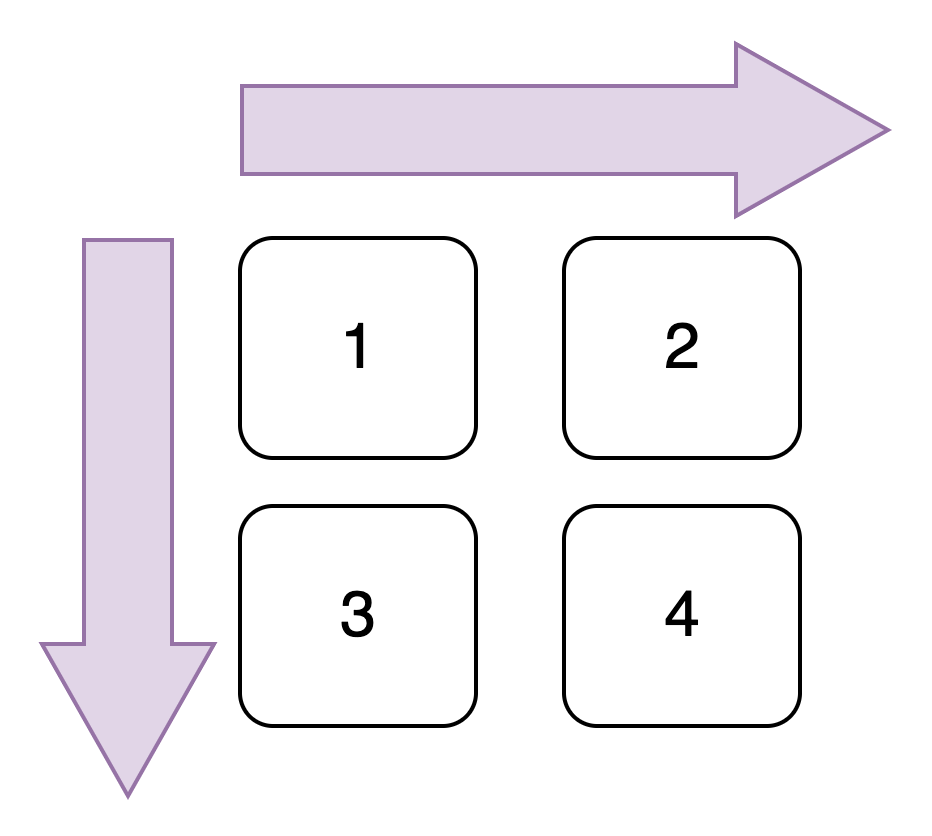
1차원 배열에서 사용한 공식을 활용하여 2차원의 배열의 경우에는 B[i][j] = B[i][j-1] - B[i-1][j] + A[i][j]라는 공식이 나오게 됩니다.

👨‍💻 구현

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class 구간합구하기2_11660 {
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static StringBuilder sb = new StringBuilder();
    static StringTokenizer st;
    static int N, M;
    static int[][] arr;
    static int[][] sumArr;

    public static void main(String[] args) throws IOException {
        inputArr();
        addArr();
        solution();
        System.out.println(sb.toString());
    }

    private static void solution() throws IOException {
        int result = 0;
        for (int i = 0; i < M; i++) {
            result = calculateArr();
            sb.append(result).append('\n');
        }
    }

    private static int calculateArr() throws IOException {
        st = new StringTokenizer(br.readLine());
        int x1 = Integer.parseInt(st.nextToken());
        int y1 = Integer.parseInt(st.nextToken());
        int x2 = Integer.parseInt(st.nextToken());
        int y2 = Integer.parseInt(st.nextToken());

        return sumArr[x2][y2] - sumArr[x1 - 1][y2] - sumArr[x2][y1 - 1] + sumArr[x1 - 1][y1 - 1];
    }

    private static void addArr() {
        for (int i = 1; i <= N; i++) {
            for (int j = 1; j <= N; j++) {
                sumArr[i][j] = sumArr[i - 1][j] + sumArr[i][j - 1] - sumArr[i - 1][j - 1] + arr[i][j];
            }
        }
    }


    private static void inputArr() throws IOException {
        st = new StringTokenizer(br.readLine());
        N = Integer.parseInt(st.nextToken());
        M = Integer.parseInt(st.nextToken());
        arr = new int[N + 1][N + 1];
        sumArr = new int[N + 1][N + 1];

        for (int i = 1; i <= N; i++) {
            st = new StringTokenizer(br.readLine());
            for (int j = 1; j <= N; j++) {
                arr[i][j] = Integer.parseInt(st.nextToken());
            }
        }
    }
}