그래프
그래프 단골 문제
bfs, dfs, prim, kruskal, dijkstra 알고리즘
최소 스패닝 트리(minimum spanning tree)
그래프가 주어졌을때 최소한의 비용으로 모든 정점을 연결하는 부분트리.
Kruskal, prim
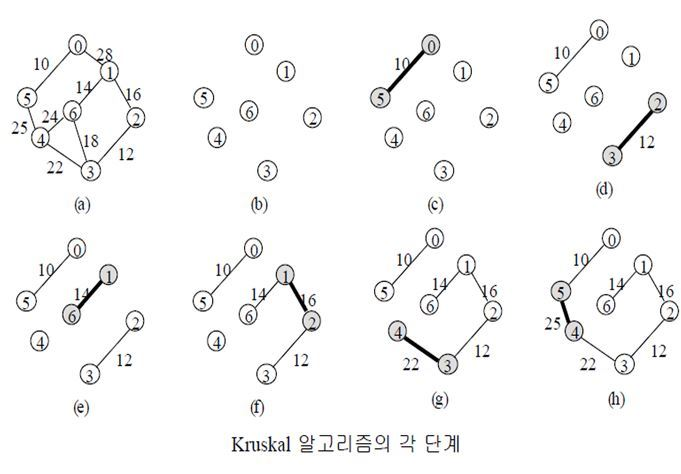
Kruskal
개념
1. 비용을 기준으로 간선을 정렬한다.
2. 간선이 잇는 두 노드의 Root노드를 찾는다.
3. Root 노드가 다르다면 연결해준다.
union find ++
이미지 출처
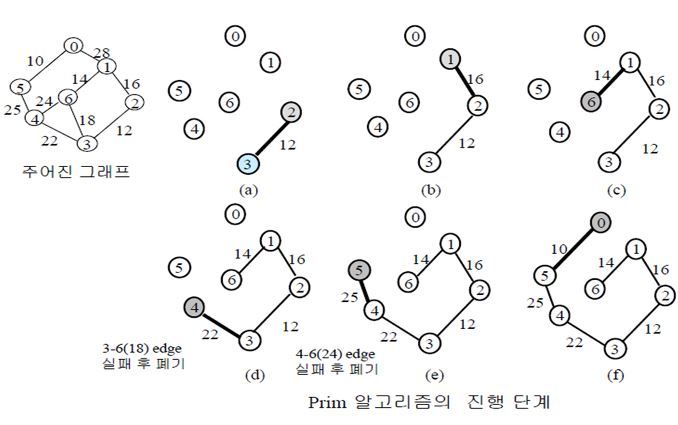
Prim
개념
1. 노드 하나 임의로 선택
2. 해당 노드에서 갈 수 있는 노드를 minheap에 넣음
3. heap에서 꺼내서 방문하지 않은 노드라면 해당 노드에서 갈 수 있는 노드를 minheap에 추가로 넣음
4. 모든 노드를 방문했으면 탈출
Kruskal vs Prim
Kruskal의 경우 cycle이 생기는지 확인하기위해 union find 알고리즘을 사용하는데 해당 알고리즘은 O(1)의 시간복잡도를 가진다. 따라서 정렬하는 알고리즘이 Kruskal의 성능을 좌지우지한다.
퀵,머지, 팀 등 빠른 정렬알고리즘의 시간복잡도는 nlogn을 따른다. 따라서 크루스칼의 시간복잡도는 O(ElogE)를 따른다.
Prim의 경우 노드에서 갈 수 있는 노드를 모두 min heap에 추가한다. 그렇다면 최대 E번 heap에 넣어야한다.
-> O(ElogV) : 모든 간선 x 간선을 통해 삽입된 가중치 기준 정렬
노드를 추가할 때 마다 heap 내부에선 heap 정렬을 진행한다.
또한 모든 노드를 탐색할때 heap에서 최소값을 pop하여 사용한다.
-> O(VlogV) : 모든 정점 x heap에서 pop
따라서 O(ElogV) + O(VlogV)의 복잡도를 가지는데
간선의 수 >= 노드의 수이기 때문에 시간복잡도는 O(ElogV)를 따른다.