시간복잡도와 빅오(Big-O)
알고리즘의 성능을 수학적으로 나타내는 표기법이다.
실제로 알고리즘의 시간을 표현할 때 사용하는 것이 아닌, 알고리즘의 성능을 예상할 때 사용한다.
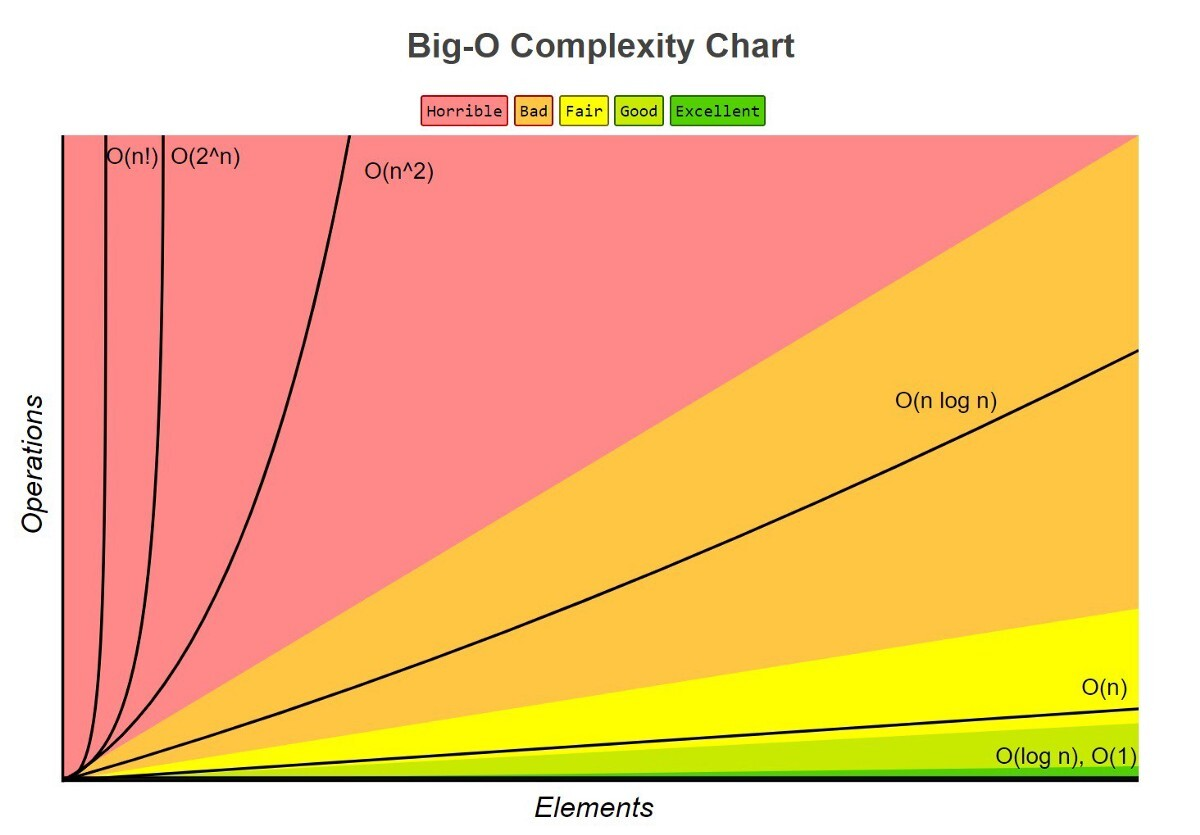
빅오와 관련된 학습을 하다보면 위와 같은 그래프를 쉽게 볼 수 있다.
그래프의 X축과 Y축을 통해, 빅오는 데이터의 증가율에 따른 알고리즘 성능을 나타낸 것임을 알 수 있다.
→ 상수와 같은 숫자들은 모두 1이 된다.
그렇다면 기본적으로 알고 있어야할 빅오 표기법의 예제에 대해 살펴보자.
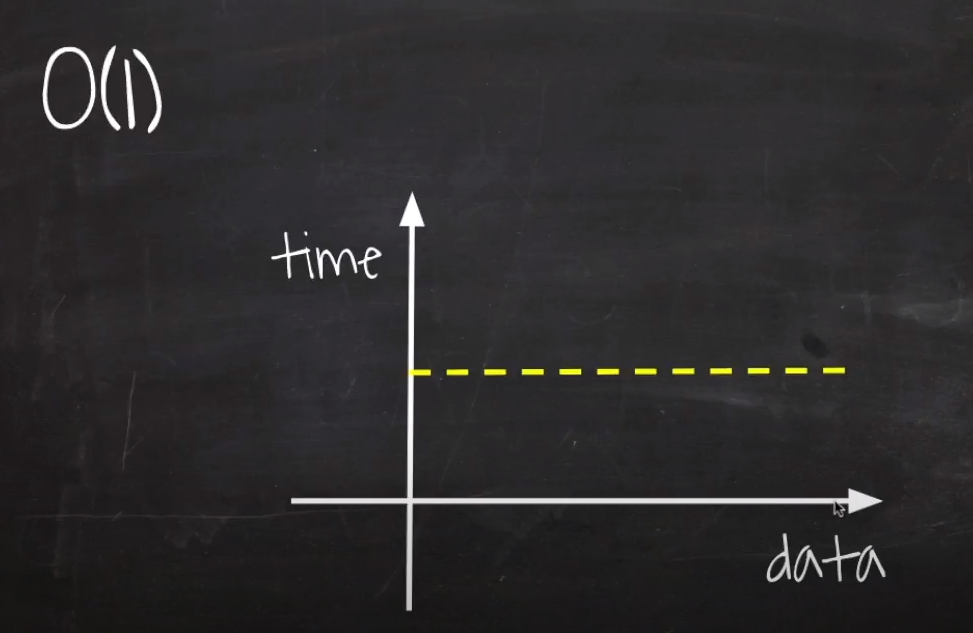
O(1) : Constant Time
입력 데이터의 크기에 상관 없이, 언제나 일정한 시간이 걸리는 알고리즘
//O(1)
const findO1 = (arr) => {
//배열의 첫 번째 인자가 0이면 true, 아니면 false 반환
return arr[0] === 0 ? true : false;
};위와 같은 함수가 있을 때, 함수의 인자로 어떤 배열이 들어오더라도 처리 시간과 성능에 변화가 없다.
이런 경우에 시간복잡도를 O(1)이라고 한다.
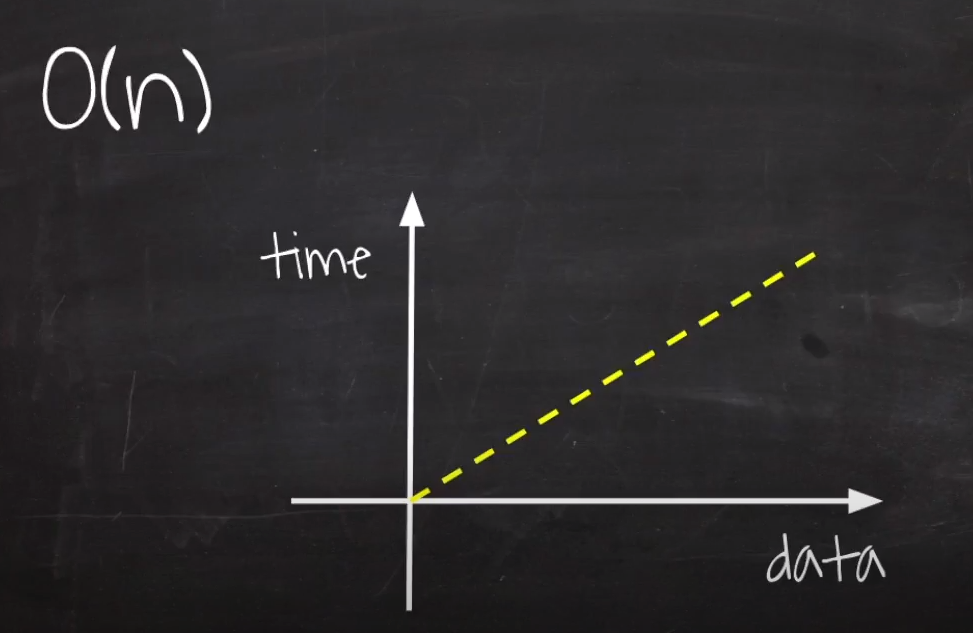
O(n) : Linear Time
입력 데이터의 크기에 비례하여, 처리 시간이 증가하는 알고리즘
//O(n)
const findO2 = (arr) => {
//arr 배열을 돌면서 원소 모두 출력
arr.map((a) => console.log(a));
};위와 같은 함수가 있을 때, 함수의 인자로 들어오는 배열의 크기가 커지면 커질 수록 처리 시간은 정비례하게 증가한다.
이런 경우에 시간 복잡도를 O(n)이라고 한다.
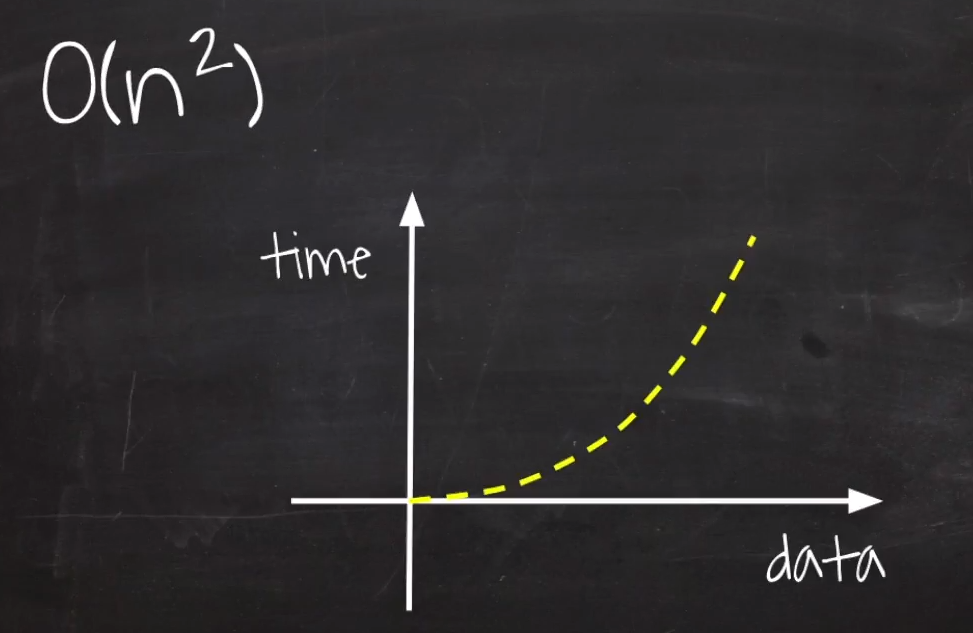
O(n^2) : Quadratic Time
입력 데이터의 크기의 제곱만큼 비례하여, 처리 시간이 증가하는 알고리즘
//O(n^2)
const findO3 = (array) => {
array.forEach((arr) => {
arr.forEach((a) => {
console.log(a);
});
});
};위 함수에서, 인자로 이차원 배열이 들어오는 경우 배열의 크기가 커지면 커질수록 처리 시간은 제곱하여 증가한다.
인자로 들어오는 배열의 크기가 작다면 처리 시간이 그리 오래걸리지 않지만, 크기가 커질수록 처리 시간이 기하급수적으로 증가한다.
O(nm) : Quadratic Time
O(n^2)와 유사하지만, m 값에 따라 크게 달라질 수 있다.
하지만, 빅오에서는 추정치를 기반으로 하기 때문에 O(n^2)의 그래프와 동일하게 표현된다.
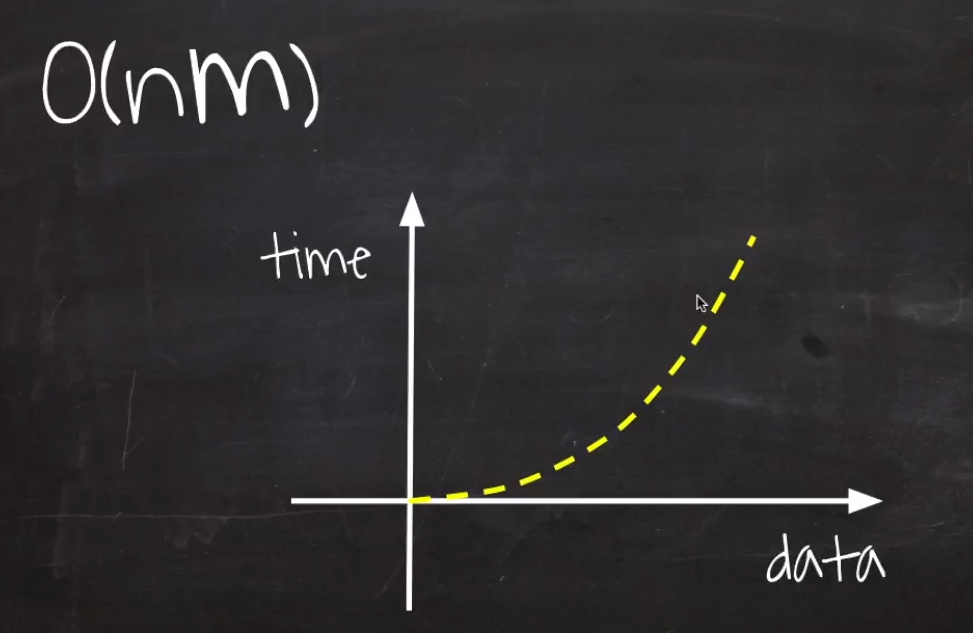
O(n^2)에서 사용한 forEach문은 모든 원소를 도는 루프문이다.
때문에 일반적인 for문을 사용하는 것이 아니라면 위의 에제와 동일하게 표현될 수 있으므로, 해당 예제는 생략한다.
O(n^3) : Polynomial / Cubic Time
O(n^2), O(nm)의 원리와 동일하다.
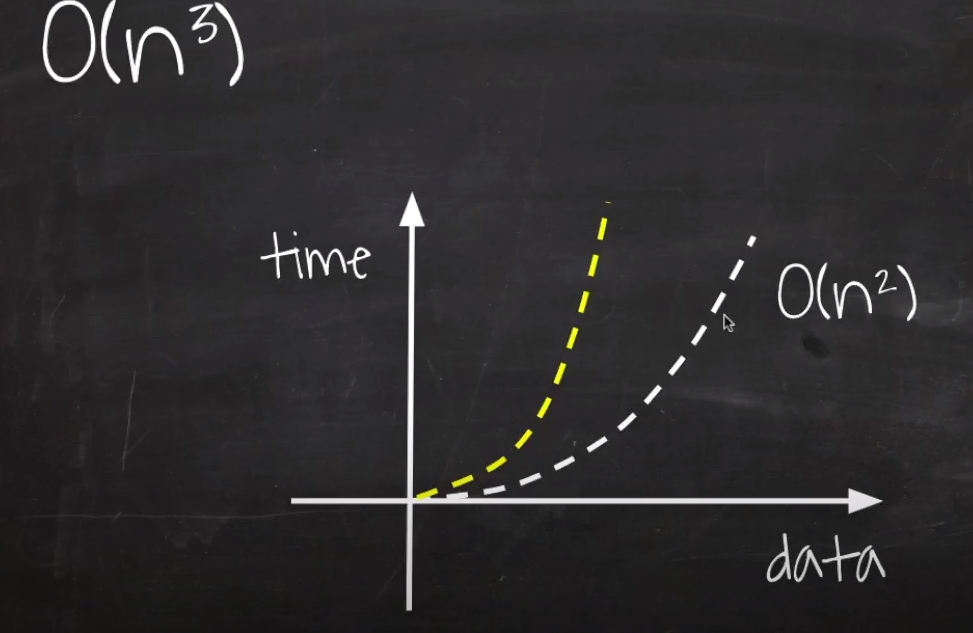
위의 Quadratic Time과 다른 점은 그래프가 더 빨리 가파라진다는 것이다.
O(nm)과 동일하게, 예제는 생략한다.
O(2^n) : Exponential Time
피보나치 수열과 같은, 재귀 함수를 떠올려보자.
함수에서 두번의 재귀 구문이 있다면, n(트리의 높이)만큼 탐색을 진행하기에 시간복잡도는 O(2^n)이 된다.
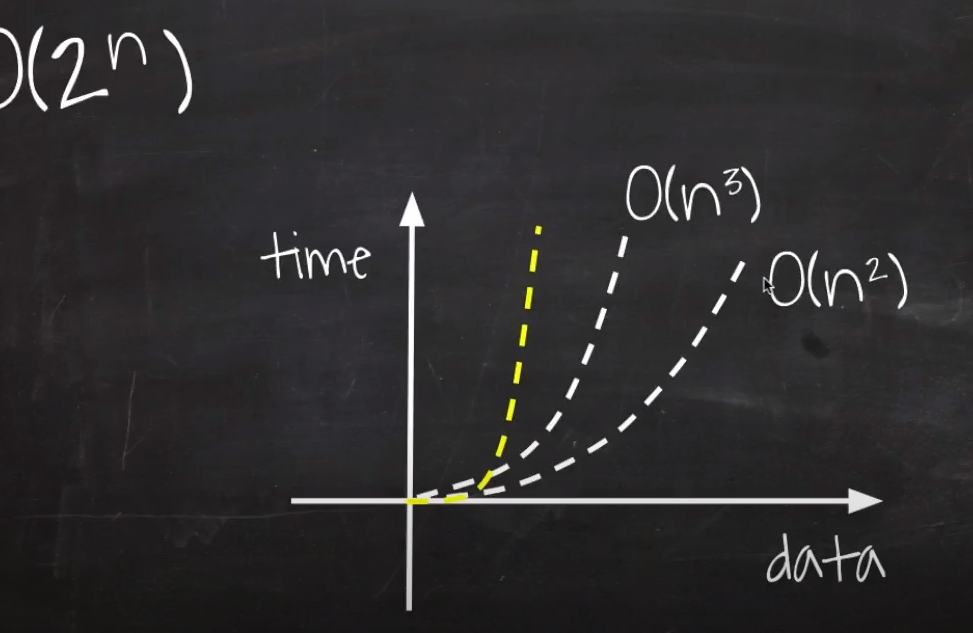
//O(2^n)
const findO4 = (n) => {
//피보나치 수열
if (n <= 0) return 0;
else if (n === 1) return 1;
return findO4(n - 1) + find(n - 2);
};피보나치 수열 예제 코드이다.
피보나치 수열의 트리 구조는 아래 그림과 같다.
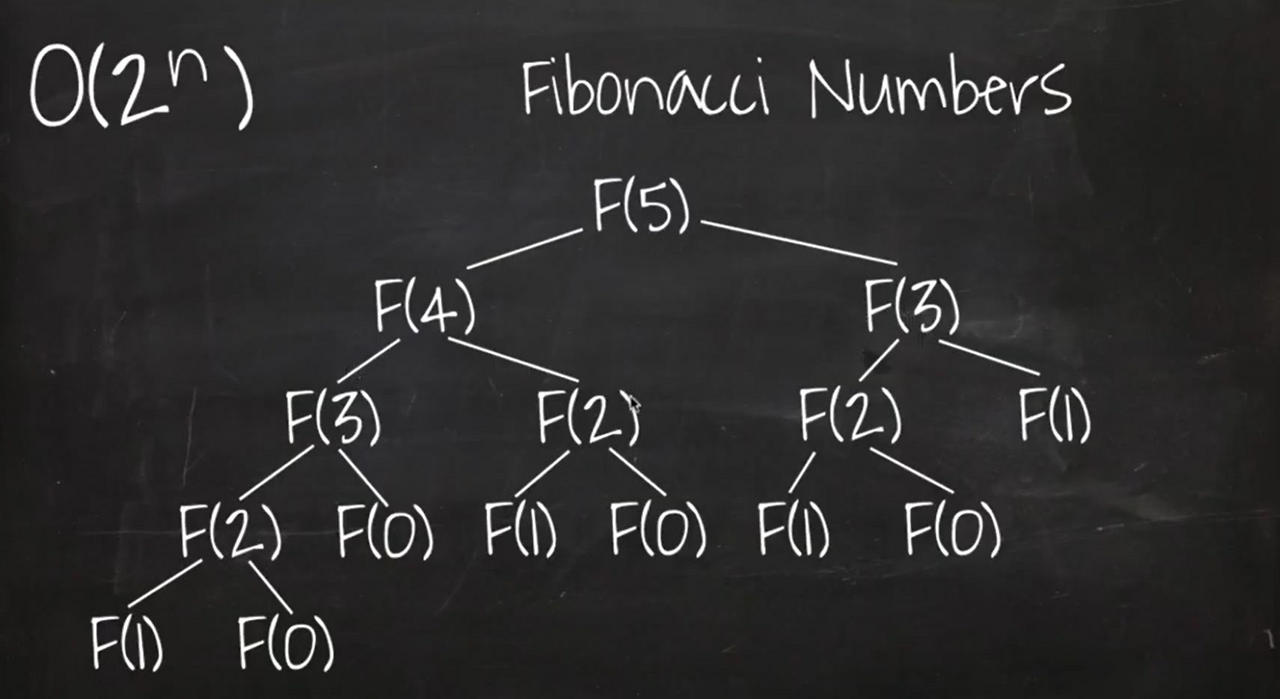
매번 함수가 호출 될 때마다, 2번씩 또 호출하는데 이를 트리의 높이만큼 반복하면 피보나치 수열이다.
그리고 이것의 시간복잡도가 곧 O(2^n)이 되며, 이 경우 시간복잡도의 증가율이 앞선 것들보다 훨씬 가파르다.
O(m^n) : Exponential Time
위 O(2^n)과 유사하지만, 함수가 호출되는 횟수가 다른 경우 사용된다.
경우에 따라 O(2^n) 보다 그래프 기울기가 가파를 수 있다.
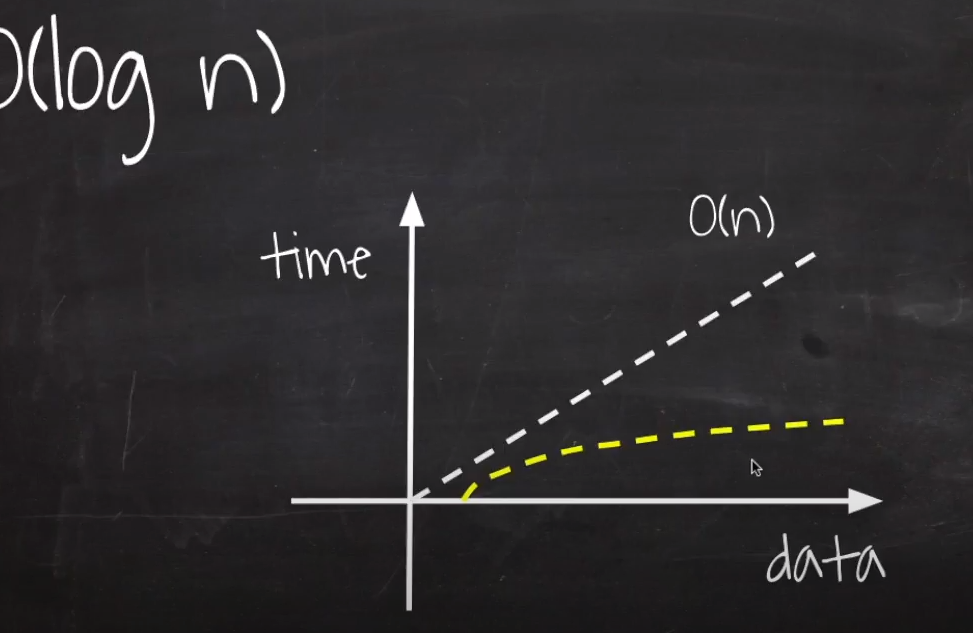
O(logn)
이진탐색 알고리즘과 같은 경우에 시간 복잡도는 O(logn)이 된다.
//O(logn)
const findO5 = (key, start, end) => {
for (let i = start; i <= end; i++) {
arr.push(i);
let m = (start + end) / 2;
if (arr[m] === key) {
console.log(m);
} else if (arr[m] > key) {
return findO5(key, start, m - 1);
} else {
return findO5(key, m + 1, end);
}
}
};- 배열의 가운데 값과 키값을 비교
- 대소에 따라서, 가운데 이전 혹은 가운데 이후 요소들 중 한쪽을 없앰
- 나머지 요소에서 또 가운데 값과 키값을 비교
- 반복
이렇게 한 번 반복 할 때마다, 처리해야하는 값이 절반씩 사라지는 알고리즘의 시간복잡도를 O(logn)이라고 한다.
데이터가 증가해도 성능에 큰 차이가 없음을 알 수 있다.
O(sqrt(n)) : Square Root
자연수 n이 소수임을 판별하는 경우, n을 2부터 n-1 까지 나누어보지 않아도 된다.
sqrt(N)까지만 나누어 봐도 소수임을 판별할 수 있는데, 이 경우 해당 알고리즘의 시간 복잡도는 O(sqrt(n))이 된다.
//O(sqrt(n))
const isPrime = (num) => {
if (num === 2) {
return true;
}
for (let i = 2; i <= Math.floor(Math.sqrt(num)); i++) {
if (num % i === 0) {
return false;
}
}
return true;
};모든 소수 판별 / 약수 찾기 등의 알고리즘은 O(sqrt(n))의 시간 복잡도를 갖는다.
이에 대한 자세한 정리는 후에 알고리즘을 공부하며 하도록 한다.
🐸 빅오에서 중요한 점 : Drop Constant
빅 오 표기법의 핵심은 함수의 러닝타임이 아닌 처리시간의 증가율을 예측하는 것이다.
때문에 상수가 나온다면? 과감히 버린다.
//Drop Constant
const findO6 = (arr) => {
//arr 배열을 돌면서 원소 모두 출력
arr.map((a) => console.log(a));
arr.map((a) => console.log(a));
};가령 위와 같은 코드에서, 시간 복잡도는 O(2n)이 될 것이라 예측할 수 있을 것이다.
하지만 실질적인 표기는 결국 O(n)으로 한다는 것이다.
끝으로
우선 모든 알고리즘의 기초가 되는 빅 오 표기법에 대해 정리해보았습니다.
사실 개념적으로 대충은 알고있었지만, 이렇게 깔끔하게 복기하고 넘어가니 좋네요!
글 작성하며 참고한 자료는 아래 첨부하였습니다. 직접 들어보는 것도 좋을 것 같아요.

