-
Q. Bayesian 확률을 정의해봐라.
A. 사전정보 또는 데이터를 통해 확립한 이론에 새로운 데이터를 첨가하는 이론에 기반한 통계이다. -
Q. Frequentist 확률을 정의해봐라.
A. 사전정보와 상관없이 실제 시행착오를 통한 통계이다. -
Q. Bayesian 정리가 왜 인공지능에 중요한지 설명해봐라.
A. 모델을 학습시킬때 파라미터를 업데이트시키는 과정에 새로운 데이터를 받아들일때 이전의 상태에 따라 달라지기 때문에 이에는 frequentist 이 아니라 bayesian 을 접목을 해야합니다.
인공지능 공부를 하다보면 베이즈 확률에 대한 이야기를 계속 듣게 된다. 계속 뭔가 얼렁뚱땅 넘어가는 것만 같아서 이번에는 확실하게 정리를 하고 넘어가고 싶다.
Bayes Probability , 베이즈 통계학.
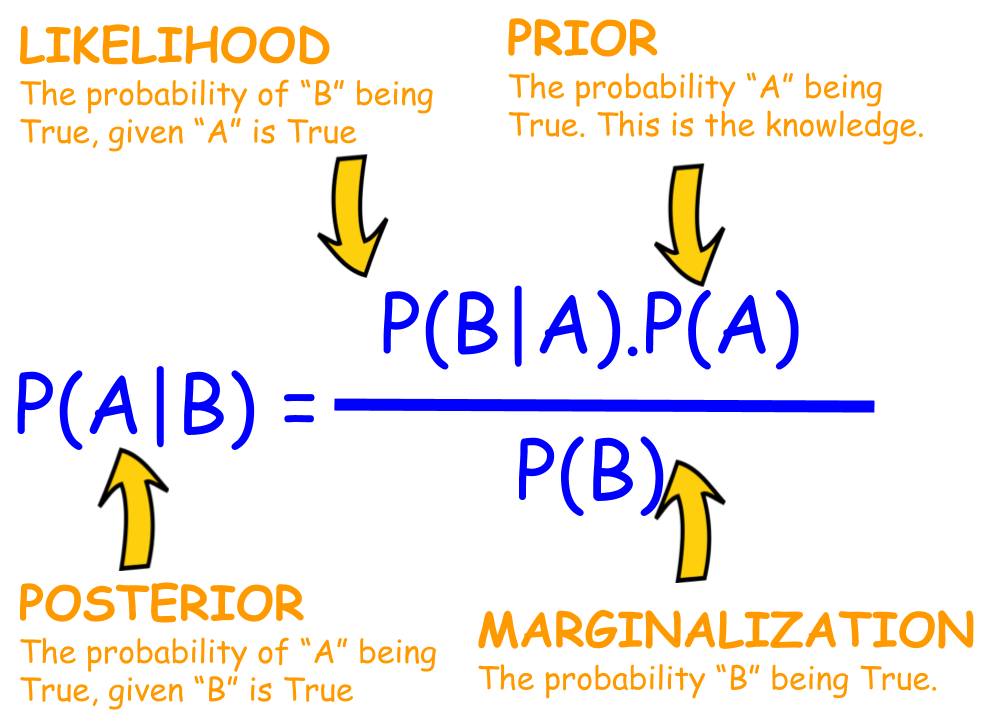
베이즈 정리란 한 마디로 사전정보 또는 데이터를 통해 사후확률을 예측하는 과정에서 사용되는 공식을 말합니다. 즉, 실제로 하는 것이 아니라 이전의 상태에 따른 통계입니다.
베이즈 통계학은 사후 확률을 추론하는 방식인 베이즈 정리를 이용해 통계학의 문제에 접근하는 것을 말한다. 이때 베이즈 정리는
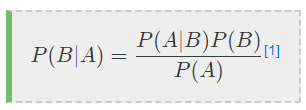
와 같은 식으로 정리 될 수 있다.
베이즈 통계학의 반대인 Frequentist Probability 을 알면 더 잘 이해할 수 있다.
Frequentist Probability 은 실제에 더 기반한 통계고 Bayes Probability 은 이론 및 가설에 기반한 통계이다.
Q. 동전을 뒤집어서 위 면이 숫자가 나올 확률은?
Frequentist 나 Bayes 둘 다 0.5, 또는 절반이라 대답한다.
동전을 뒤집고나서...
Q. 지금 내 손에 있는 동전의 위 면이 숫자가 나올 확률은?
Bayes 의 대답은 여전히 0.5, 절반. 이라고 할 것이지만
Frequentist 은 지금은 알 수 없지만 그 확률은 0 또는 1 이며 확인하고나서 확실해진다. 라고 대답할 것이다.
이처럼 Bayes 은 이론에 더 치중된 통계학이다.
이런 Bayes Probability 가 머신러닝 및 AI 에 매우 중요한 이유는 베이즈 통계를 이용해 새로운 데이터가 들어오면 그 데이터를 현재 있는 모델의 파라미터에 맞게 수정을 해 학습을 하기 때문이다. 다른 말로, 현재의 모델에 기반해 새로운 데이터가 일으키는 변화가 달라진다는 것이다.
이때 Bayes Probability 을 이용해 학습은 시키는데 위의 식에 기반한 계산이 아니라 Markov Chain Monte Carlo Method 을 이용해 update 시킨다.