
SciPy
Collection of packages that provide useful mathematical functions commonly used for scientific computing.
유용한 함수(수학적)를 제공하는 패키지 모음이다.
List of subpackages
- cluster : Clustering algorithms (군집화 알고리즘)
- constants : Physical and mathematical constants (물리 및 수학 상수)
- fftpack : Fast Fourier Transform routines
- integrate : Integration and ordinary differential equation solvers (적분 및 일반 미분 풀이)
- interpolate : Interpolation and smoothing splines (보간 및 평활 스플라인)
- io : Input and Output (입력 및 출력)
- linalg : Linear algebra (선형 대수)
- ndimage : N-dimensional image processing (N차원 이미지 프로세싱)
- odr : Orthogonal distance regression (직교 거리 회귀 분석)
- optimize : Optimization and root-finding routines (최적화 및 루트 찾기 루틴)
- signal : Signal processing (신호 처리)
- sparse : Sparse matrices and associated routines (희소 행렬 및 관련 루틴)
- spatial : Spatial data structures and algorithms (공간 자료 구조 및 알고리즘)
- special : Special functions (특수 함수)
- stats : Statistical distributions and functions (통계적 분포 및 함수)
많은 서브패키지 중에서도
interpolate
optimize
stats
integrate
에 대해 살펴 볼 예정이다.
Interpolation : scipy.interpolate
import scipy.interpolate as interpx = np.linspace(-1, 2, 5);
y = x**3
plt.plot(x, y, 'bo')를 실행해보면
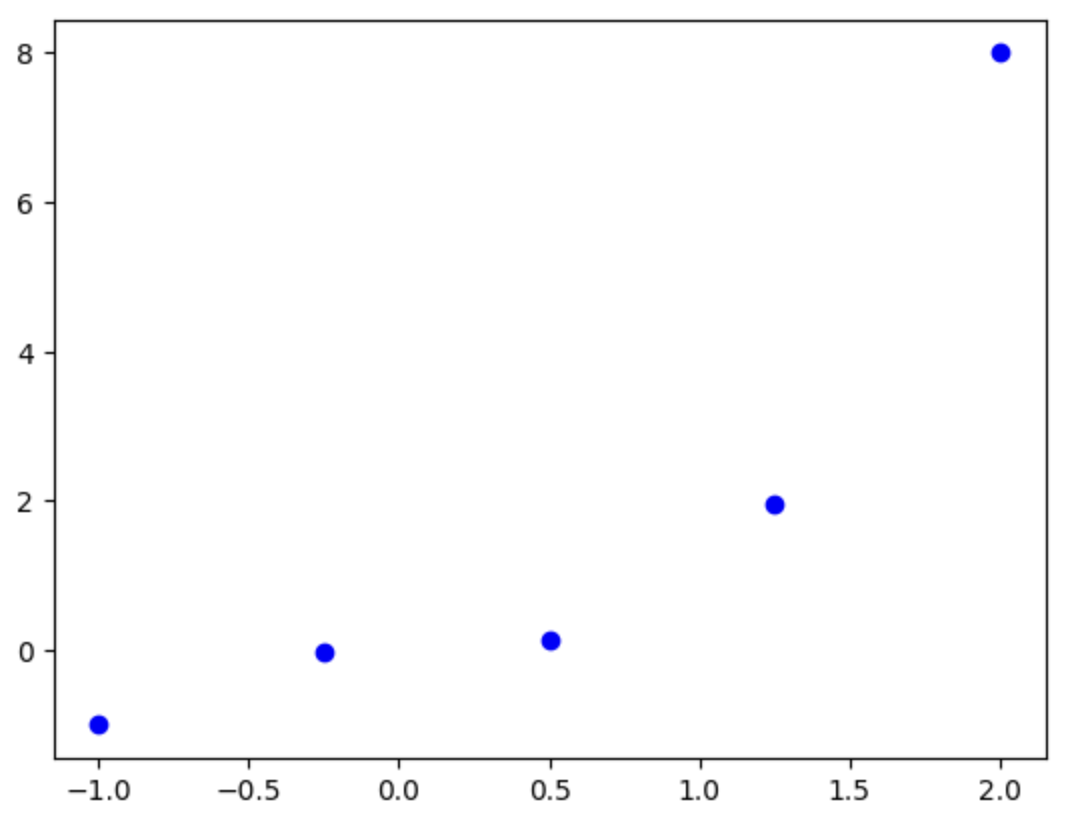
위와 같은 결과가 나온다.
이제 'scipy.interpolate'를 사용해보자.
f = interp.interp1d(x,y,kind="linear")interp.interp1d(x, y, kind="linear") 는 주어진 (x, y) 데이터 포인트에 대한 선형 보간 함수를 생성한다. x는 입력값, y는 이에 대응하는 출력값이다. kind="linear"는 선형 보간 방법을 사용한다는 것을 의미한다. 따라서 f는 입력 x 값을 받아 해당하는 선형 보간된 y 값을 반환하는 함수라고 할 수 있겠다.
x_fine = np.linspace(-1,2,100)
plt.plot(x_fine,f(x_fine))
plt.plot(x,y,'ro')따라서 위의 코드를 실행해보면 다음과 같은 결과가 출력된다.
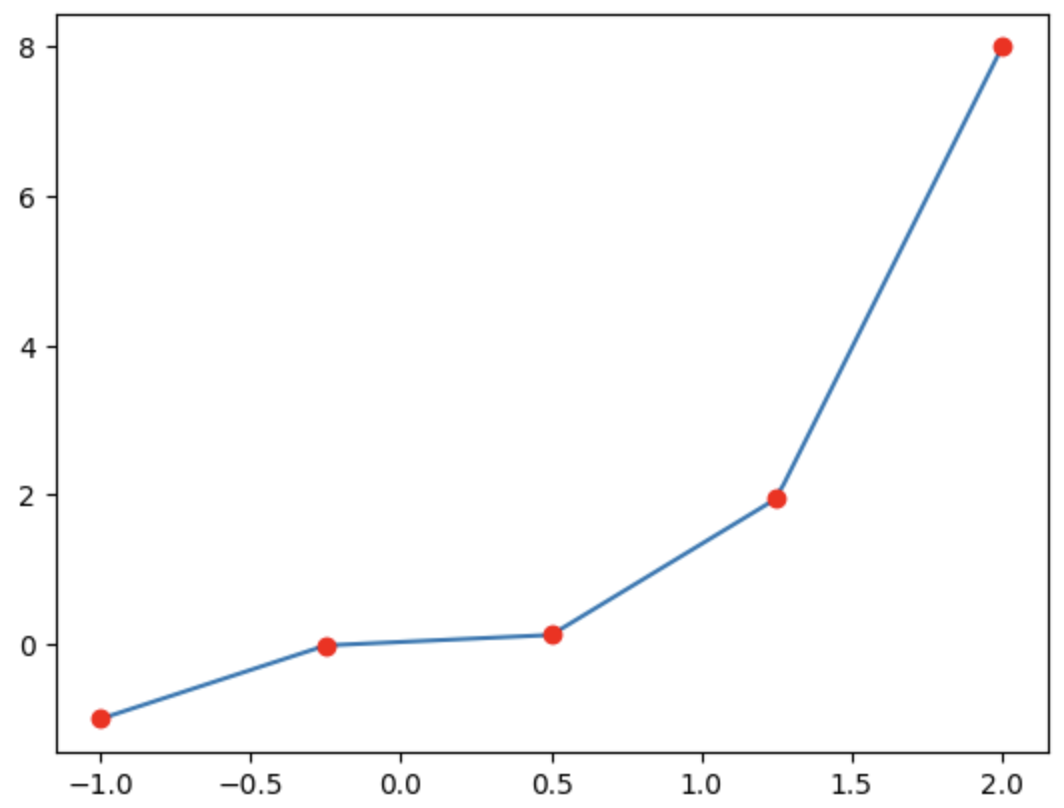
x_fine = np.linspace(-1, 2, 100) 은 -1과 2 사이를 100개의 동일한 간격으로 나눈 배열을 생성하는 코드이다.
plt.plot(x_fine, f(x_fine)) 는 x_fine을 x축으로, f(x_fine)을 y축으로 하는 그래프를 생성한다. f(x_fine)은 아까 언급했듯, x_fine 배열에 대한 보간된 y 값들을 반환한다. 따라서 x_fine에 대한 보간된 그래프가 그려진다.
Optimization : scipy.interpolate
from scipy import optimizedef f(x):
return x**4 - 10*x**2x = np.linspace(-5, 5, 100)
plt.plot(x, f(x))x = np.linspace(-5, 5, 100) 는 -5부터 5까지를 100개의 동일한 간격으로 나눈 배열을 생성한다.
plt.plot(x, f(x)) 는 배열 x와 이에 해당하는 f(x)값을 각각 x축 y축으로 하는 그래프를 그린다. 이는 다음과 같다.
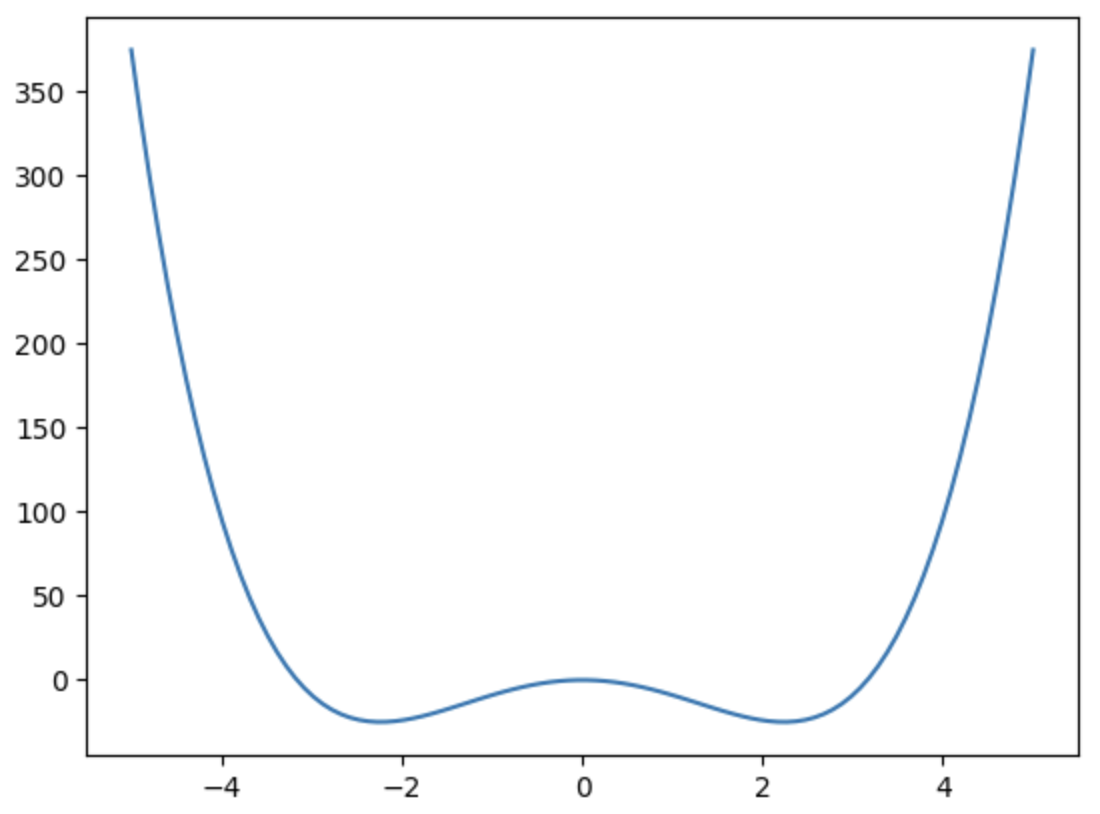
results = optimize.minimize(f, 4)optimize.minimize(f, 4) 는 함수 f를 최소화하는 값을 찾기 위한 최적화 알고리즘을 실행한다. 초기 추정값으로 4를 사용하게 되고 results 변수에 최적화 알고리즘의 실행 결과가 저장된다.
x_opt = results.xx_opt = results.x 는 최적화 알고리즘의 실행 결과에서 최적해를 가져와 x_opt 변수에 저장한다. results.x는 최적화 알고리즘을 통해 얻은 최적해를 의미한다.
plt.plot(x,f(x));
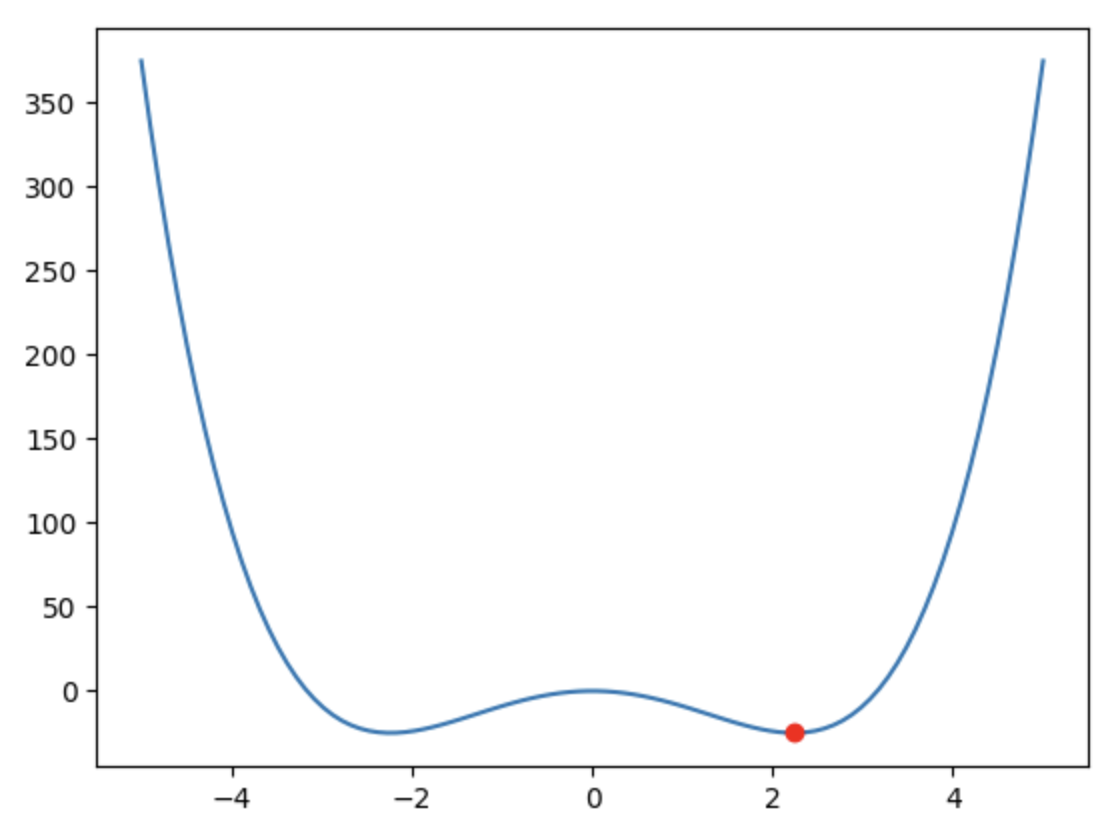
plt.plot(x_opt,f(x_opt),'ro');plt.plot(x, f(x)) 는 x를 x축으로, f(x)를 y축으로 하는 그래프를 그려준다.
plt.plot(x_opt, f(x_opt), 'ro') 는 x_opt를 x축으로, f(x_opt)를 y축으로 하는 그래프를 그린다. (x_opt, f(x_opt)) 좌표에 빨간색 동그라미로 표시된 점이 그려진다.
결과는 다음과 같다.
def f(x):
return x[0]*x[0] + x[1]*x[1] + 5*(np.sin(2*x[0]) + np.sin(2*x[1]))x = np.linspace(-5,5,100)
y = np.linspace(-5,5,100)
X,Y = np.meshgrid(x,y)X, Y = np.meshgrid(x, y) 는 x와 y 배열로부터 2차원 그리드를 생성한다. X는 x를 열 방향으로 복제한 결과를, Y는 y를 행 방향으로 복제한 결과를 가지는 2차원 배열이다. 이렇게 생성된 X와 Y는 f 함수를 2차원 입력으로 계산하기 위한 그리드를 형성한다.
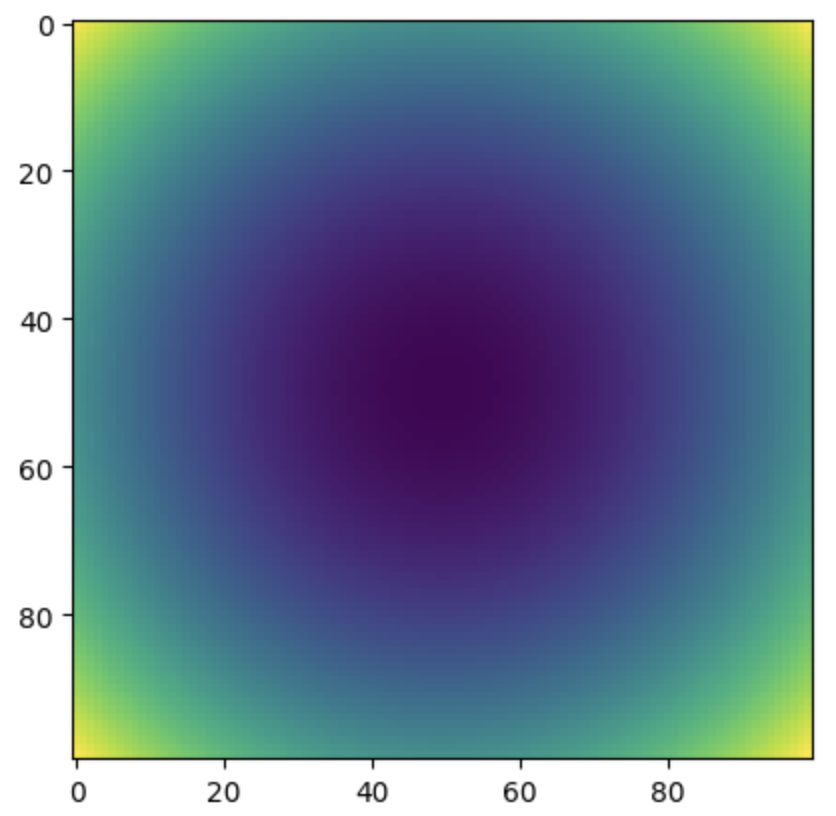
plt.imshow(X**2+Y**2)plt.imshow(X2 + Y2) 는 X의 제곱과 Y의 제곱을 더한 값을 이미지로 나타낸다. imshow() 함수는 2차원 배열을 이미지로 표현하는 함수인데, 이를 통해 (X, Y) 그리드 상의 각 점에 대해 X의 제곱과 Y의 제곱의 합을 색상으로 표현한 이미지를 생성하는 것이다.
실행 결과는 다음과 같다.
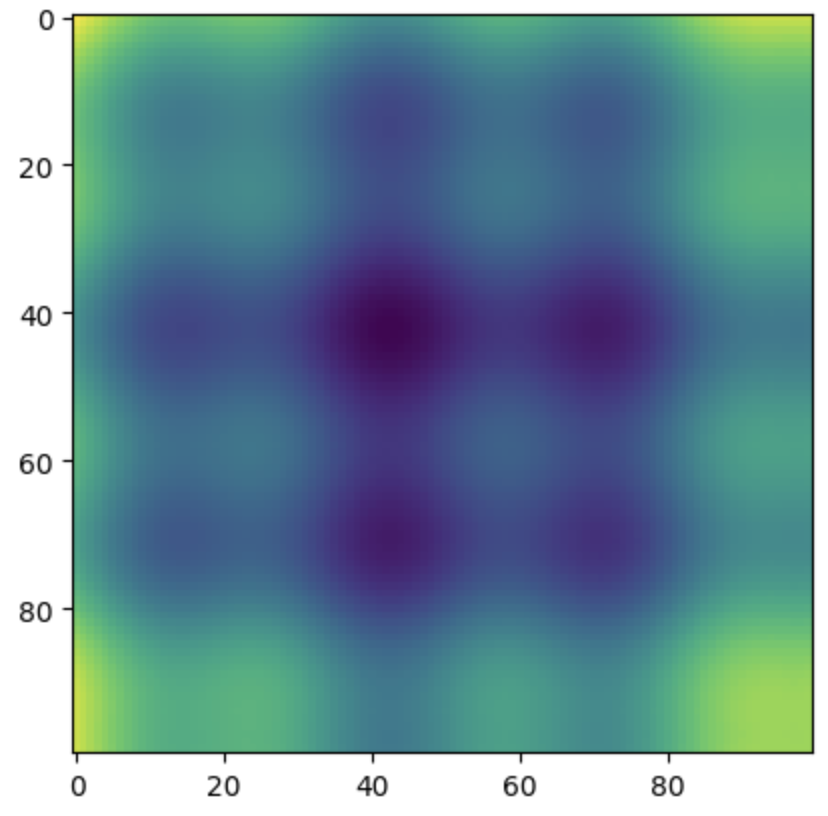
plt.imshow(f(np.array([X,Y])))plt.imshow(f(np.array([X, Y]))) 는 X와 Y로 구성된 2차원 배열을 f 함수에 전달하여 각 그리드 포인트에서의 함수 값을 계산한다. np.array([X, Y])는 X와 Y를 합쳐서 shape가 (2, 100, 100)인 배열을 생성하며, 이 배열은 f 함수에 전달되어 각 점에서의 함수 값을 계산하게 된다. plt.imshow() 함수는 2차원 배열을 이미지로 표시하는 함수이므로 여기서는 f 함수를 통해 계산된 값을 이미지로 나타낼 수 있다.
결과는 다음과 같다.
Curve Fitting
x = np.linspace(-2,2,30)
y = x+np.sin(6.5*x)+0.3*np.random.randn(30)
plt.plot(x,y,'ro')x = np.linspace(-2, 2, 30) 는 -2부터 2까지를 30개의 동일한 간격으로 나눈 배열을 생성한다.
y = x + np.sin(6.5*x) + 0.3*np.random.randn(30) 는 x에 대응하는 y 값을 계산하는데, x 값과 사인 함수(np.sin)를 사용한 항, 그리고 정규 분포에서 추출한 임의의 노이즈(0.3*np.random.randn(30))를 더하여 y 값이 생성된다.
def f(x,a,b):
return a*x +b((a,b),_) = optimize.curve_fit(f,x,y,(0,0))x_fine = np.linspace(-2,2,200)
plt.plot(x_fine,f(x_fine,a,b))
plt.plot(x,y,'ro')def g(x,a,b):
return a*x +b*np.sin(6.5*x)((a,b),_) = optimize.curve_fit(g,x,y,(0,0))x_fine = np.linspace(-2,2,200)
plt.plot(x_fine,g(x_fine,a,b))
plt.plot(x,y,'ro')