
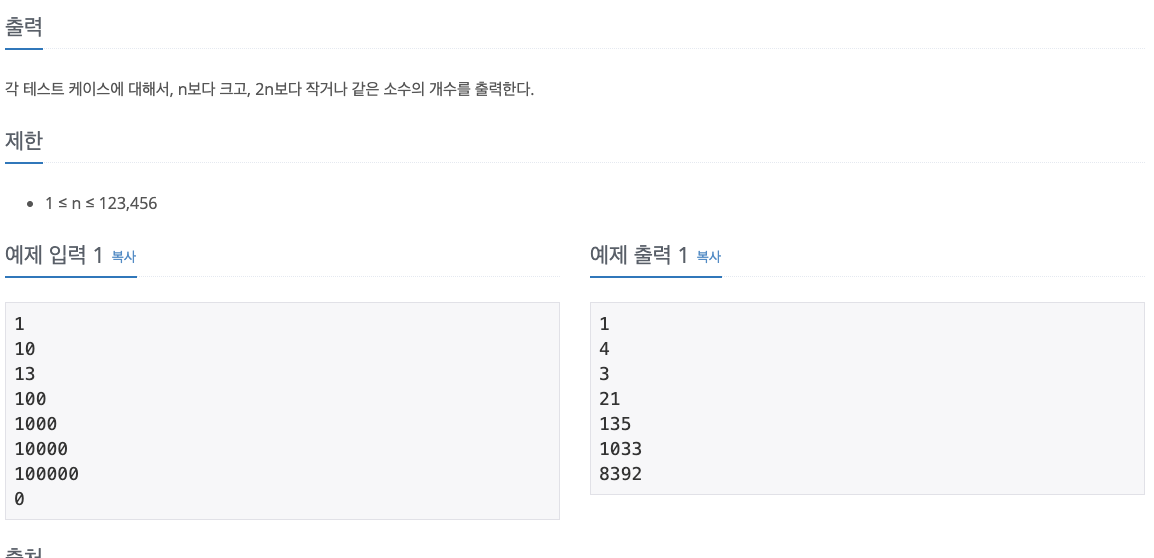
이번 문제는 n 부터 2n까지 소수를 구하는 문제 입니다.
이 문제는 위의 소수 구하기 문제에서 범위를 한정하는 것만 추가된
문제입니다.
해당 문제를 풀었을 때에는 x**0.5 로 루트 씌우는 걸 활용하요
제곱근외에 다른 약수가 없는 경우 출력하는 방법으로 풀었습니다.
이번에도 그와 같은 방식으로 풀었고,
문제에 추가된 것과 같이 범위를 추가하였습니다.
def sosu(x):
if x ==1: #1은 모든 수의 약수이기 때문에 pass
return False
for i in range(2,int(x**0.5)+1): #제곱근이 있는 수 중에
if x%i==0: #약수가 있으면 false
return False
return True #이외에는 소수
while True:
n = int(input()) #범위를 주기 위한 입력
count=0
if n == 0 : #0 입력하면 아웃되는 게 조건
break
for i in range(n,2*n+1): #n과 2n+1사이에서
if sosu(i): #sosu함수안에 있는 게 있다면
count+=1 #카운트를 세라
print(count) #개수를 출력하는 조건에 맞춰 카운트를 출력처음에는 이런 식으로 모든 소수를 구하고 입력 받은 n값 안에서의
소수를 찾게 했는데 시간 초과가 떴습니다.
크게 손보지 않는 한에서 해결 방안은 모든 소수가 아닌
문제에서 제한한 범위 1 <= n <=123,456 안에서의 소수만 저장하고
for 문을 돌리는 동안 소수 리스트에 있는 소수들을 꺼내오는 방식으로
풀었습니다.
def sosu(n):
if n ==1:
return False
for i in range(2,int(n**0.5)+1):
if n%i==0:
return False
return True #소수 구하는 방식은 위와 같다
all_list = list(range(2,246912)) #문제에서 제한한 범위
memo = [] #for문 밖에 리스트 정의
for i in all_list: #2부터 2*123,456 범위
if sosu(i): #sosu함수에 해당하면
memo.append(i) #리스트에 추가
n = int(input())
while True:
count=0 #갯수를 세야하는 조건 때문에 카운트
if n == 0 :
break
for i in memo: #memo리스트 중에서
if n < i <=2*n: #입력한 값의 범위 내에서 값이 있으면
count+=1 #있을 때 마다 카운트 +1
print(count)
n = int(input()) #0 입력받기 전까지 계속 해야하므로 입력 받음

