[TIL] CSAPP 2.4 부동소수점

부동소수점이란?

• Floating-Point 은 실수를 !근사적! 표현 하는 방법
• 컴퓨터는 데이터를 2진수로 저장하므로, 실수 또한 2진수로 저장\

부동소수점의 구조

부위	설명	예시(32bit)
부호 비트	양수/음수 구분	1비트
지수(exponent)	수의 크기 범위 조절	8비트
가수(fraction,mantisssa)	실제 숫자 정보	23비트

값 계산 공식

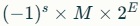
s: 부호 비트(0=양수, 1=음수)
E: 지수(지수 비트에서 bias를 뺀 값)
M: 가수(1 + fraction)

특징과 한계

1.정확한 실수 표현 불가 : 2진수로는 2^-1,-2,-3 식으로 0.5, 0.25, 0.125 밖에 표현만 가능하기에 근사값만 저장

반올림 오차 : 연산 결과가 표현 범위를 벗어나면 반올림됨
오버플로우/언더플로우 : 너무 큰 값(오버플로우)이나 너무 작은 값(언더플로우)는 표현이 불가

정규화

부동소수점 값은 정규화되어 저장.
이진수에서는 가수의 첫 자리가 항상 1이 되도록 표현해서, 그 1을 저장하지 않고(숨겨진 비트) 공간을 절약

지수의 바이어스

지수는 음수도 표현해야 하므로, 실제 지수에 바이어스를 더해 저장.
즉, 저장된 값 = 실제 지수 + 바이어스.

바이어스란?

지수부분에서도 필요한 음수를 표현하기위해 덧대는 값
실제 지수 0 → 저장값 127 (0 + 127)
실제 지수 -3 → 저장값 124 (-3 + 127)
실제 지수 5 → 저장값 132 (5 + 127)

특수값

• 0 : 모든 비트가 0이거나, 부호만 다르고 나머지가 0일 때 0또는 -0을 표현.
• infinity(무한대): 지수 all 1, 가수 all 0
• NaN : 지수 all 1,가수 중 1이라도 1
• 비정규화 수 : 지수 all 0, 가수에 1이 있음. 아주 작은 수를 표현할 때 사용 3 5

표현의 정밀도

부동소수점은 넓은 범위의 수를 표현할 수 있지만, 유효 숫자(가수 비트 수) 만큼만 정밀하게 저장할 수 있음.

대부분의 실수는 2진수로 정확히 표현할 수 없음 오차 누적될 수 있음
오차 누적과 비슷한 느낌으로 연산은 덧셈,곱셈 순서에 따라 결과가 달라질 수 있음.

부동소수점 연산

• 연산 (+,-,*,/)시 항상 반올림이 발생할 수 있음.
• 덧셈,곱셈 등은 내부적으로 정규화(normalization), 반올림(rounding) 과정을 거침.

예)
float에서 0.1 + 0.2 == 0.3

• false가 나옴 (근사값 오차)

이유)

• 부호 0 (양수)
• 2진수: 110.1
• 정규화 : 1.101 × 2²
• 지수 : 2+127(bias)=129 -> 10000001
• 가수 : 101(이후 0으로 채움)
• 최종 비트: 0 10000001 10100000000000000000000

float의 지수 부분이 모두 1이고 가수 부분이 0이 아닐 때, 이 수는 무엇을 의미하는가?
NaN (Not a Number)

Nan에 대해

계산 불능, 정의되지 않은 값, 예를 들어 0으로 나누기, 0/0, sqrt(-1)등에서 발생.
NaN이란 무엇인가?
Not a Number은 부동소수점 표준에서 "숫자가 아닌 값" 을 의미
NaN은 계산 결과가 수학적으로 정의되지 않거나, 표현 할 수 없는 경우에 사용

NaN의 비트 패턴
지수 비트가 모두 1, 가수 비트가 0이 아님.