아주아주 코딩이 잘 되는 하루!
알고리즘 문제 링크
https://programmers.co.kr/learn/courses/30/lessons/17676
문제
문제 설명
추석 트래픽
이번 추석에도 시스템 장애가 없는 명절을 보내고 싶은 어피치는 서버를 증설해야 할지 고민이다.
장애 대비용 서버 증설 여부를 결정하기 위해 작년 추석 기간인 9월 15일 로그 데이터를 분석한 후
초당 최대 처리량을 계산해보기로 했다.
초당 최대 처리량은 요청의 응답 완료 여부에 관계없이 임의 시간부터 1초(=1,000밀리초)간 처리하는 요청의 최대 개수를 의미한다.
입력 형식
solution 함수에 전달되는 lines 배열은 N(1 ≦ N ≦ 2,000)개의 로그 문자열로 되어 있으며,
각 로그 문자열마다 요청에 대한 응답완료시간 S와 처리시간 T가 공백으로 구분되어 있다.
응답완료시간 S는 작년 추석인 2016년 9월 15일만 포함하여 고정 길이 2016-09-15 hh:mm:ss.sss 형식으로 되어 있다.
처리시간 T는 0.1s, 0.312s, 2s 와 같이 최대 소수점 셋째 자리까지 기록하며 뒤에는 초 단위를 의미하는 s로 끝난다.
예를 들어, 로그 문자열 2016-09-15 03:10:33.020 0.011s은 "2016년 9월 15일 오전 3시 10분 33.010초"부터 "2016년 9월 15일 오전 3시 10분 33.020초"까지 "0.011초" 동안 처리된 요청을 의미한다. (처리시간은 시작시간과 끝시간을 포함)
서버에는 타임아웃이 3초로 적용되어 있기 때문에 처리시간은 0.001 ≦ T ≦ 3.000이다.
lines 배열은 응답완료시간 S를 기준으로 오름차순 정렬되어 있다.
출력 형식
solution 함수에서는 로그 데이터 lines 배열에 대해 초당 최대 처리량을 리턴한다.
입출력 예제
예제1
입력: [
"2016-09-15 01:00:04.001 2.0s",
"2016-09-15 01:00:07.000 2s"
]
출력: 1
예제2
입력: [
"2016-09-15 01:00:04.002 2.0s",
"2016-09-15 01:00:07.000 2s"
]
출력: 2
설명: 처리시간은 시작시간과 끝시간을 포함하므로
첫 번째 로그는 01:00:02.003 ~ 01:00:04.002에서 2초 동안 처리되었으며,
두 번째 로그는 01:00:05.001 ~ 01:00:07.000에서 2초 동안 처리된다.
따라서, 첫 번째 로그가 끝나는 시점과 두 번째 로그가 시작하는 시점의 구간인
01:00:04.002 ~ 01:00:05.001 1초 동안 최대 2개가 된다.
예제3
입력: [
"2016-09-15 20:59:57.421 0.351s",
"2016-09-15 20:59:58.233 1.181s",
"2016-09-15 20:59:58.299 0.8s",
"2016-09-15 20:59:58.688 1.041s",
"2016-09-15 20:59:59.591 1.412s",
"2016-09-15 21:00:00.464 1.466s",
"2016-09-15 21:00:00.741 1.581s",
"2016-09-15 21:00:00.748 2.31s",
"2016-09-15 21:00:00.966 0.381s",
"2016-09-15 21:00:02.066 2.62s"
]
출력: 7
설명: 아래 타임라인 그림에서 빨간색으로 표시된 1초 각 구간의 처리량을 구해보면
(1)은 4개, (2)는 7개, (3)는 2개임을 알 수 있다.
따라서 초당 최대 처리량은 7이 되며, 동일한 최대 처리량을 갖는 1초 구간은 여러 개 존재할 수 있으므로
이 문제에서는 구간이 아닌 개수만 출력한다.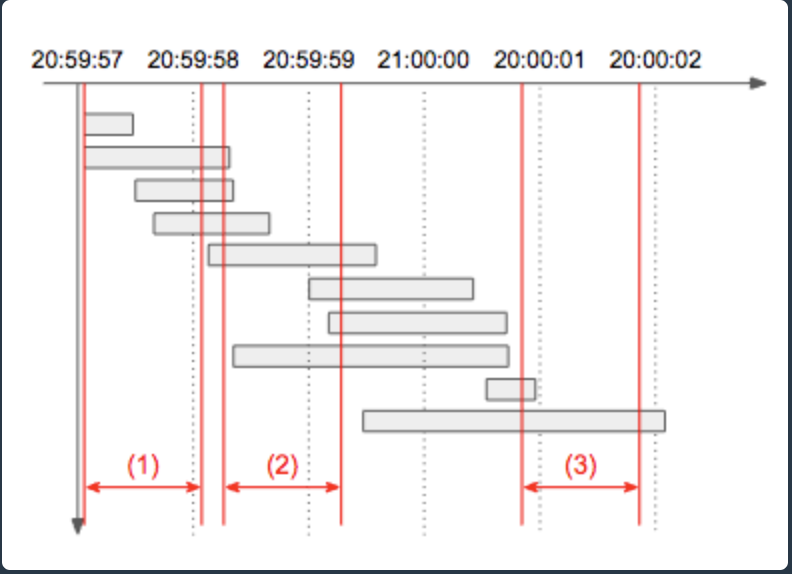
해결코드
function solution(lines) {
const excuteList = [];
let max = 0;
// 로그 데이터의 시작,종료 시간을 처리시간을 통해 구함
for(let i=0; i< lines.length; i++){
const lineSplit = lines[i].split(' ');
const endAt = `${lineSplit[0]} ${lineSplit[1]}`;
const endDate = new Date(endAt).getTime();
const duration = Number(lineSplit[2].slice(0, -1) * 1000);
const startDate = new Date(endDate - duration + 1).getTime();
excuteList.push([startDate, endDate]);
}
// 처리시간의 시작, 종료 시점을 기준으로 앞, 뒤로 1초의 섹션을 만들어서
// 해당 섹션에 속하는 로그가 존재하면 최대 처리 개수 추가
for( let i=0; i < excuteList.length; i++){
// 주석1. 1초간 처리할 수 있는 구간은 로그의 시작, 종료 시점으로부터 1초 전, 후이다.
const start = excuteList[i][0];
const startAfterSection = [start, start + 1000];
const startBeforeSection = [start - 1000, start];
const end = excuteList[i][1];
const endAfterSection = [end, end + 1000];
const endBeforeSection = [end - 1000, end];
max = getSectionMaxExec(excuteList, startAfterSection, max);
max = getSectionMaxExec(excuteList, startBeforeSection, max);
max = getSectionMaxExec(excuteList, endAfterSection, max);
max = getSectionMaxExec(excuteList, endBeforeSection, max);
}
return max;
}
// 전체 로그에서 해당 섹션에 속하는 로그의 개수를 구하고, 최대 처리량과 비교 후 최대 처리량을 반환
function getSectionMaxExec(excuteList, currentSection, max){
let currentMax = 0;
for(let j=0; j < excuteList.length; j++){
const anotherSection = excuteList[j];
// 해당 섹션의 외곽에 있는 경우가 아니라면, 속한 것으로 판정.
if(!(anotherSection[1] <= currentSection[0] || anotherSection[0] > currentSection[1])){
currentMax++;
}
}
return currentMax > max ? currentMax : max;
}추가설명
특정 구간이 정해져있지 않은 1초를 어떻게 정할 지 생각하면 금방 풀 수 있는 문제
주석1.
위에서 설명한 내용처럼, 특정 구간이 정해져 있지 않은 1초내의 처리량을 구하는 문제이므로,
어디서부터 1초를 잡아야할 지 기준을 정하는 구간이다.
조금만 생각해보면, 로그의 시작과 끝에서 전, 후로 1초가 기준이됨을 알 수 있다.
S-----------------E
|--------------|
|--------------|
|--------------|
|--------------|
|--------------| : 1초나올 수 있는 경우의 수는 위의 허접한 그림과 같다.
잡담
어제 효율성은 완전히 실패하고, 조건을 달성하는 부분까지만 완성했었는데,
오늘은 어제의 최악의 코드를 전부 지우고, 다시 코드를 작성했다.
처음에는 불특정 1초 구간을 정하는 문제가 너무 선형적인 느낌이라서 어떻게 코드로 구현해야 할 지 막막했었는데,
그 구간이 나올 수 있는 부분은 한정되어 있을 것이다라는 생각에 도달하는 순간 문제는 순식간에 풀렸다.
다 풀고 나서, 베스트 코드와 속도를 비교했을 때도 내 코드가 더 빨랐다!
1000 ms 이나, 중복된 함수 사용은 조금 더 유연하고 효율적으로 수정할 수 있겠지만, Skip~~
오늘은 머리가 잘 굴러가는 날이였다 ~
