기초 수학

1) 집합 (Set)
특정 조건에 맞는 원소들 모임

• 집합 표현 방법
  원소 나열 법 -> A ={1,2,3,4,5} B={2,4,6,8,10}
  조건 제시법
  A = {A|A는 정수, 1<=A<=5}
  B = {2B|B 는 정수, 1<=B<=5}

집합에는 교집합, 합집합, 여집합, 차집합이 있다.

2) 경우의 수
어떤 사건에서 일어날 수 있는 경우의 수
사건 A가 일어날 경우의 수: n(A)
ex) 동전을 던지는 사건 = 2

• 합의 법칙 n(A u B)
  사건 A 또는 사건 B가 일어날 경우의 수
  사건 A와 B의 합의 법칙
  단 중복 사건이 있을 경우 빼줘야 함

-곱의 법칙 n(A x B)
사건 A와 사건B가 동시에 일어날 경우의 수

3) 순열

• Factorial
  1에서 n까지 모든 자연수의 곱 (n!)
  1! = 1
  2! = 1 x 2
  n! = n(n-1)(n-2)

-순열(Permutation)
순서를 정해서 나열
서로 다른 n개 중에 r개를 선택 하는 경우의 수 (순서o , 중복 x)

-> nPr = n!/(n-r)! = n(n-1)(n-2) .... (n-r+1)
단) 0<=r<=n

ex)
5명을 3줄로 세우는 방법
=5 x 4 x 3
서로 다른 4명 중 반장, 부반장 뽑는 방법
반장 : 4 x 3
부반장: 3 x 2
= 4P3 = 4! / (4 - 2)!

-중복순열
서로 다른 n개 중 r개를 선택하는 경우의 수 (순서 o, 중복 o)
ex) 서로 다른 4개의 수 중 2개를 뽑는 방법(중복 허용)
= 4 x 4

nπr = n의 r 제곱

-원 순열 (n!/n) = (n-1)!
원 모양의 테이블에 n개의 원소를 나열하는 경우의 수
ex) 원 모양의 테이블에 3명을 앉히는 경우
ABC = BCA = CAB
BAC = ACB = CBA

4) 조합 ( nCr = n!/(n-r)r! = nPr/r!
-조합(Combination)
서로다른 n개 중에서 r개를 선택하는 경우의 수 (중복x , 순서x)

ex)
서로 다른 4명 중 2명 뽑는 방법
A B C D
o o
x x

-중복 조합 (nHr = n+r-1Cr)
서로다른 n개중 r개를 선택하는 경우의 수(순서X, 중복 O)

ex)
후보 2명, 유권자 3명일때 무기명 투표 방법
A B | 1,2,3 -> AAB, ABA는 동일하기 때문에 하나로 처리
A A A
A A B
A B A -> 2H3 = 4C3 = 4!/(4 - 3)!3!
A B B
B B B
.....

5) 점화식과 재귀함수

-점화식 (Recuurence)
어떤 수열의 일반항을 그 이전의 항들을 이용하여 정의한 식
ex) 피보나치 수열
1, 1, 2, 3, 5, 8, 13 ...
F1=F2=1, Fn+2 = Fn+1 +Fn

-재귀함수
어떤 함수가 자신을 다시 호출
반환타입 함수 이름 (매개변수) {
종료조건
...
함수이름(...)
}

-> 함수 내부에서 이 함수를 다시 호출 => 반복문
(자기 함수를 계속 호출 -> 종료함수)

6) 지수와 로그
-제곱, 제곱근, 지수
제곱 = 같은 수를 두 번 곱함, 거듭제곱: 같은 수를 거듭 곱함

-제곱근(=root)
=a를 제곱하여 b가 될때 까지 a를 b의 제곱근이라 함
2의 3승 = 2 x 2 x 2

-로그
logab
a가 b가 되기 위해 제곱해야 하는 수

7)알고리즘 복잡도
-복잡도
알고리즘 성능을 나타내는 척도
시간 복잡도 -> 알고리즘의 필요 연산 횟수
공간 복잡도 -> 알고리즘의 필요 메모리
시간 복잡도와 공간 복잡도 = Trade-Off

-> 시간 복잡도
어떤 문제를 해결하기 위한 알고리즘의 필요 연산 횟수
빅오 표기법을 통해 나타남

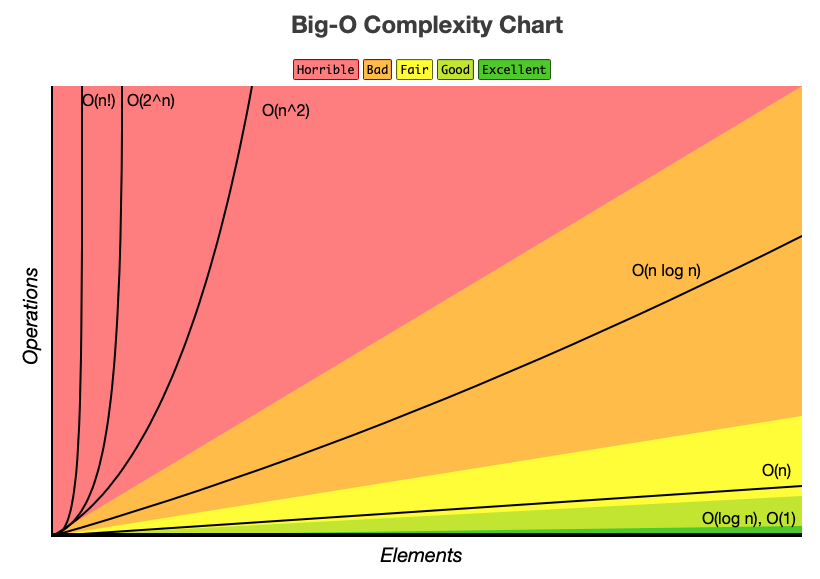
• O(c) 또는 O(1) : 상수 시간 알고리즘
  (constant time algorithm)
  • O(log n) : 로그 시간 알고리즘
    (logarithmic time algorithm)
  • O(n) : 선형 시간(1차 시간) 알고리즘
    (linear time algorithm)
  • O(n log n) : n 로그 시간 알고리즘
    (nlogn time algorithm)
  • O(n2) : 평방 시간(2차 시간) 알고리즘
    (quadratic time algorithm)
  • O(n3) : 3차 시간 알고리즘
  • O(2n) : 지수 시간
  • O(n!) : 계승 시간 (Factorial Time Algorithm)
  • O(∞) : 종료되지 않는 무한 루프

-공간복잡도
어떤 문제를 해결 하기 위해 알고리즘의 필요 메모리 사용량
빅오 표기법을 통해 나타낸다.

int[] a = new int [1000];
int[][] a = new int[1000][1000];