코딩테스트 그래프 문제에서 자주 나오는 개념이라 한번 정리해보자

플로이드-워셜 알고리즘

개념

• 플로이드-워셜(Floyd-Warshall) 알고리즘
• 모든 노드간의 최단 경로를 계산할 때 사용하는 알고리즘
• 매 단계마다 현재 노드를 거쳐 가는 노드를 기준으로 알고리즘 수행
  • N번의 단계마다 $O(N) = n^2$의 연산을 통함
• 다이나믹 프로그래밍(DP; Dynamic Programming)의 특징을 이용

점화식

시간복잡도

알고리즘 과정

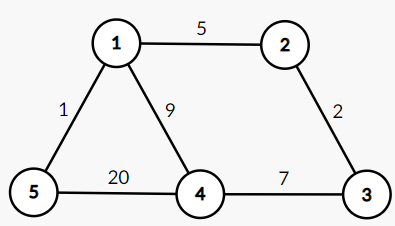
1. 2차원 인접행렬을 구성한다.
   

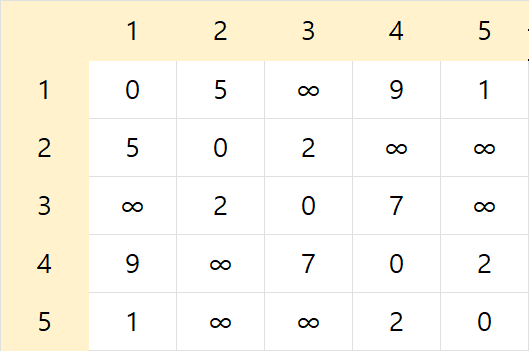
2. 모든 노드를 돌며 중간노드로 하였을때 위의 점화식을 통해 업데이트 한다.

• 1번 노드일 때
  • (2 -> 1 -> 4 == 14), (2 -> 1 -> 5 == 6)

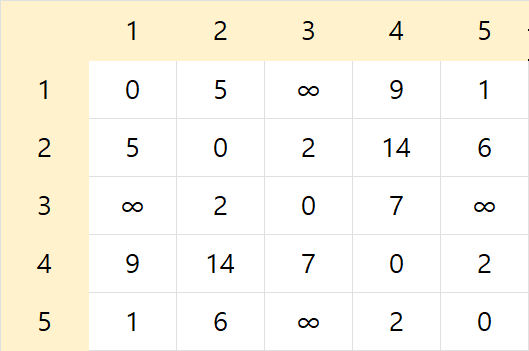
3. 나머지 모든 노드들도 같은 방법으로 업데이트!

알고리즘 구현

• 2차원 리스트에 최단거리 정보를 저장

가중치가 존재할 때

1. 최단거리 배열인 dist 배열을 초기화 한다.

• 대각 노드는 0 초기화
• 이어져 있지 않을때 주어진 조건 값 중 가장 큰 값 + 1으로 초기화

// 노드의 개수 n
// 2차원 간선 배열 adjs {{시작, 도착, 가중치}, ...}
int[][] dist = new int[n + 1][n + 1];
for (int i = 1; i < dist.length; i++) {
	for (int j = 1; j < dist[0].length; j++) {
		if (i != j) {
        	dist[i][j] = Integer.MAX_VALUE;
        }
	}
}

for (int[] adj : adjs) {
	dist[adj[0]][adj[1]] = adj[3];
    // 방향 없을 경우
    // dist[adj[1]][adj[0]] = adj[3];
}

2. 각 순회 별 중간 노드로 지정할 노드를 for문 가장 바깥 k로 지정
3. 내부 이중 for문을 통해 가중치가 작은 값으로 업데이트

for (int k = 1; k <= n; k++) {
	for (int i = 1; i <= n; i++) {
    	for (int j = 1; j <= n; j++) {
			if (distance[i][j] > distance[i][k] + distance[k][j]) {
				distance[i][j] = distance[i][k] + distance[k][j];
			}
		}
    }
}

가중치가 없을 때

• 모든 노드를 0 초기화

// 노드의 개수 n
// 2차원 간선 배열 adjs {{시작, 도착, 가중치}, ...}
int[][] dist = new int[n + 1][n + 1];

for (int[] adj : adjs) {
	dist[adj[0]][adj[1]] = 1;
    // 방향 없을 경우
    // dist[adj[1]][adj[0]] = 1;
}

• 이어져 있을 경우 1을 지정해준다.

for (int k = 1; k <= n; k++) {
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j < n; j++) {
			if (distance[i][k] == 1 && distance[k][j] == 1) {
				distance[i][j] = 1;
			}
		}
	}
}