94. Binary Tree Inorder Traversal

https://leetcode.com/problems/binary-tree-inorder-traversal/description/?envType=daily-question&envId=2023-12-10

//143ms 73.85%

import java.util.Stack

class Solution {
    
    fun inorderTraversal(root: TreeNode?): List<Int>? {
        val stack = Stack<TreeNode>()
        val result:MutableList<Int> = mutableListOf()
        
        if(root==null) {
            return result
        }
        stack.push(root)
        while(!stack.empty()) {
            traverse(stack, result)
        }
        return result
    }

    fun traverse(stack:Stack<TreeNode>, result:MutableList<Int>) {
        if(stack.peek().left!=null) {
            val node = stack.peek()
            stack.push(node.left)
            node.left = null

        } else {
            val node = stack.pop()
            result.add(node.`val`)

            if(node.right != null) {
                stack.push(node.right)
                node.right = null
            }
        }
    }
}

시간복잡도 O(n).
root node가 처음부터 null인 경우를 캐치 하지 못해서 시간이 오래걸렸다...

아이디어는 stack에 push해줄때 부모로부터 연결을 끊었다.
헤멘 부분중 하나가 push()해서 iteration할 때와, pop()해서 iteration할 때 구분을 못했었다...

중위순회(inorder)

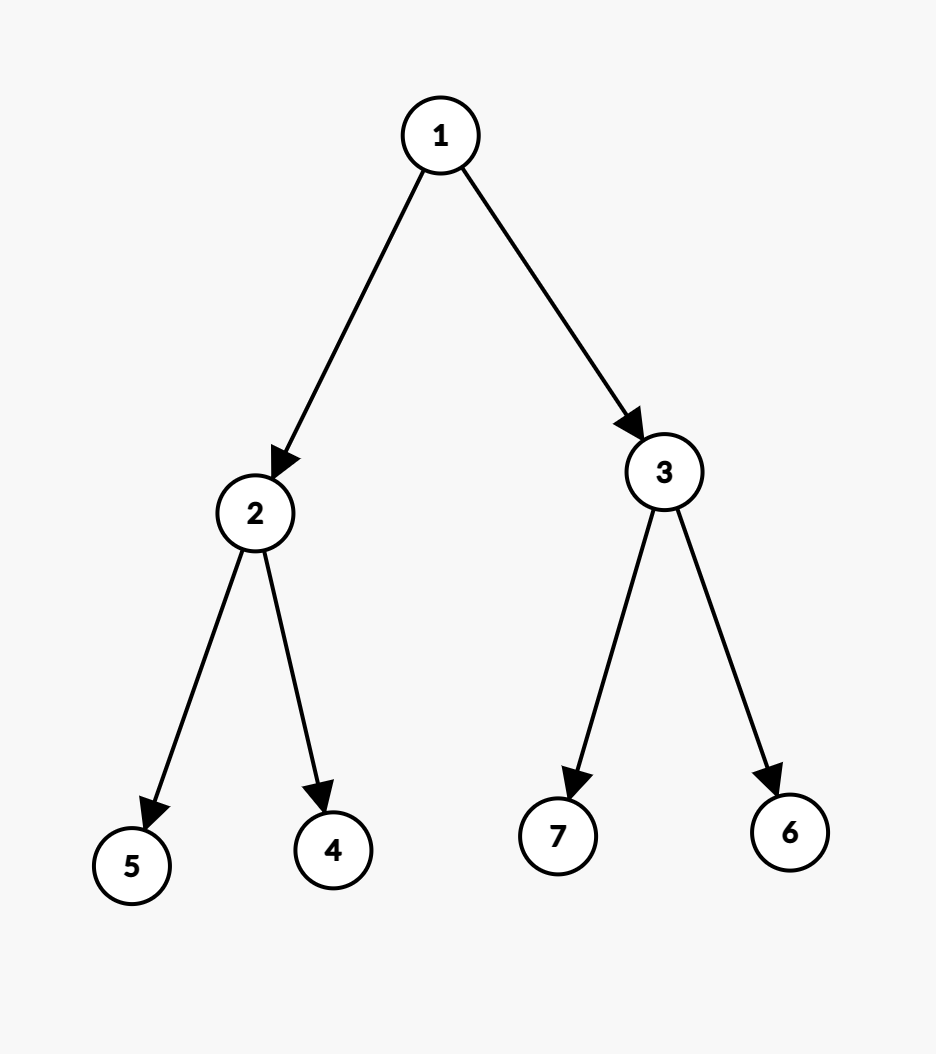
위 그래프의 중위 순회 결과는 [5, 2, 4, 1, 7, 6, 3]이다

• left -> root -> right 순서로 순회한다.
  root가 중간에 있기 때문에 중위순회라고 한다.

  전위순회(preorder): root -> left -> right
  (순회 결과: [1, 2, 5, 4, 3, 7, 6])
  후위순회(postorder): left -> right -> root
  (순회 결과: [5, 4, 2, 7, 6, 3, 1])

다른 풀이

재귀 (recursive approach)

import java.util.Stack
//136ms 89.1%
class Solution {
    
    fun inorderTraversal(root: TreeNode?): List<Int>? {
        val res:MutableList<Int> = mutableListOf()
        helper(root, res)
        return res
    }

    fun helper(root:TreeNode?, res:MutableList<Int>) {
        if(root!=null) {
            helper(root.left, res)
            res.add(root.`val`)
            helper(root.right, res)
        }
    }
}

재귀함수를 정의해서 구현한다.

재귀로 푸는 방법은 생각 해내면 쉬운데 아무래도 생각해내기 쉽지가 않다..
가독성도 그렇게 좋은느낌은 아닌듯...

iteratig method

import java.util.Stack
//132ms 94.29%
class Solution {
    
    fun inorderTraversal(root: TreeNode?): List<Int>? {
        val res:MutableList<Int> = mutableListOf()
        val stack = Stack<TreeNode>()
        var curr = root

        while(curr != null || !stack.isEmpty()) {
            while( curr != null) {
                stack.push(curr)
                curr = curr.left
            }

            curr = stack.pop()
            res.add(curr.`val`)
            curr = curr.right
        }
        return res
    }
}

내가 푼것과 같이 stack을 이용한 풀이.
나도 비슷하게 시도 했었는데 내가 틀린부분은 내 풀이에서는 left와 right를 한번에 풀려고했고, 풀이에서는 left방향을 한번에 밀어줬다.

Morris Traversal

import java.util.Stack
//122ms 99.34%
class Solution {
    
    fun inorderTraversal(root: TreeNode?): List<Int>? {
        val res:MutableList<Int> = mutableListOf()
        var curr = root
        var pre:TreeNode?

        while (curr != null) {
            if(curr.left == null) {
                res.add(curr.`val`)
                curr = curr.right
            } else {
                pre = curr.left
                while(pre!!.right != null) {
                    pre = pre.right
                }
                pre.right = curr
                val temp = curr
                curr = curr.left
                temp.left = null
            }
        }
        return res
    }
}

스택이나 재귀를 사용하지 않고 이진 트리를 중위 순회하는 방법.
각 노드의 왼쪽 자식의 가장 오른쪽 노드를 현재 노드와 연결하여 임시적인 스레드를 만들어 사용한다.
이를 Threaded Binary Tree라고 한다.

알고리즘:

• current를 root로 설정한다.
• current가 null이 아닌 동안
  • left가 null이라면
    • current.val을 list에 추가한다.
    • current를 right로 설정한다.
  • 존재한다면
    • 왼쪽 서브트리에서 가장 오른쪽 노드에 현재 노드를 오른쪽으로 연결한다.
    • left로 이동한다.