Graph traversal, [DFS, BFS]

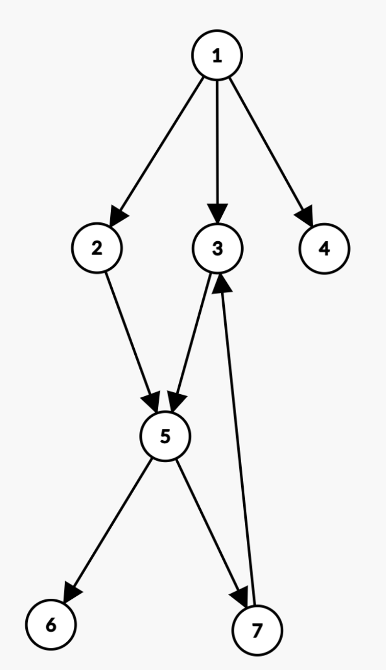
그래프의 각 정점을 방문하는 그래프 순회에는 크게 DFS와 BFS 2가지 알고리즘이 있다.

일반적으로는 BFS에 비해 DFS가 널리 사용된다.

DFS는 주로 스택으로 구현하거나 재귀포 구현하며, 백트래킹을 통해 뛰어난 효용을 보인다.

반면 BFS는 주로 큐로 구현하며, 그래프의 최적 경로를 구하는 문제 등에 사용된다.

DFS

재귀로 표현

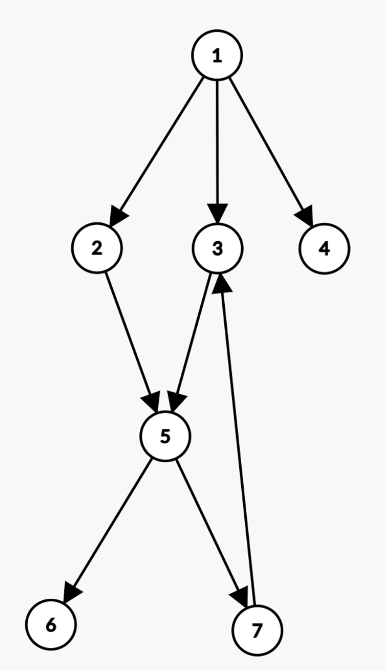
graph = {
    1: [2, 3, 4],
    2: [5],
    3: [5],
    4: [],
    5: [6, 7],
    6: [],
    7: [3]
}

def recursive_dfs(v, discovered=[]):
    discovered.append(v)
    for w in graph[v]:
        if w not in discovered:
            discovered = recursive_dfs(w, discovered)
    return discovered

스택으로 표현

def iterative_dfs(start_v):
    discovered = []
    stack = [start_v]
    while stack:
        v = stack.pop()
        if v not in discovered:
            discovered.append(v)
            for w in graph[v]:
                stack.append(w)
    return discovered

BFS

def iterative_bfs(start_v):
    discovered = [start_v]
    queue = [start_v]
    while queue:
        v = queue.pop(0)
        for w in graph[v]:
            if w not in discovered:
                discovered.append(w)
                queue.append(w)
    return discovered

BFS는 재귀로는 구현할 수 없다. 큐를 이용하여 구현하거나 좀더 최적화를 위해서 deque같은 자료구조를 사용하여 구현할 수 있다.

Backtracking

해결책에 대한 후보를 구축하며 진행하다, 가능성이 없다고 판단된다면, 즉시 후보를 포기해 정답에 더 빠르게 찾아가는 범용적인 알고리즘으로 제약 충족 문제에 유용하다.

백 트래킹은 주로 재귀로 구현하며, 기본적으로 DFS범주에 속한다.

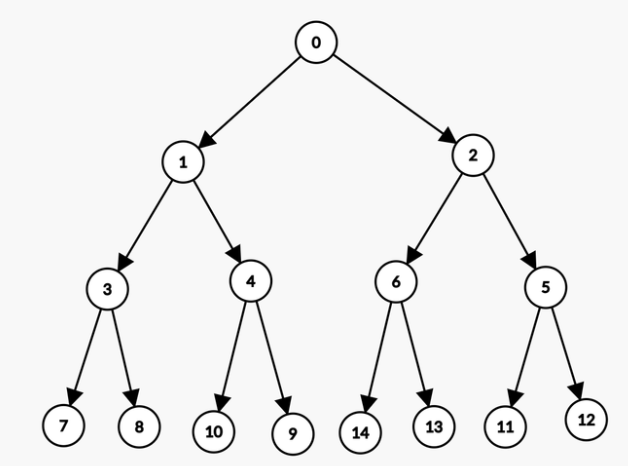
큰 트리가 있을 때, 브루트 포스로 전체 트리를 탐색하면 매우 긴 시간이 소요되지만, DFS로 탐색하면서 가능성 없는 노드를 즉시 포기하고 백트래킹한다면 불 필요한 탐색을 줄일 수 있다. 이를 트리의 Pruning이라고 한다.

제약 충족 문제 Constraint Satisfaction Problems (CSP)

백 트래킹은 CSP를 푸는데 필수적인 알고리즘이다.