Chapter 2. Red-Black Trees(RB Trees) Search (6)

1. 2-3-4 트리의 특징

2. Red-Black Trees 의 특징

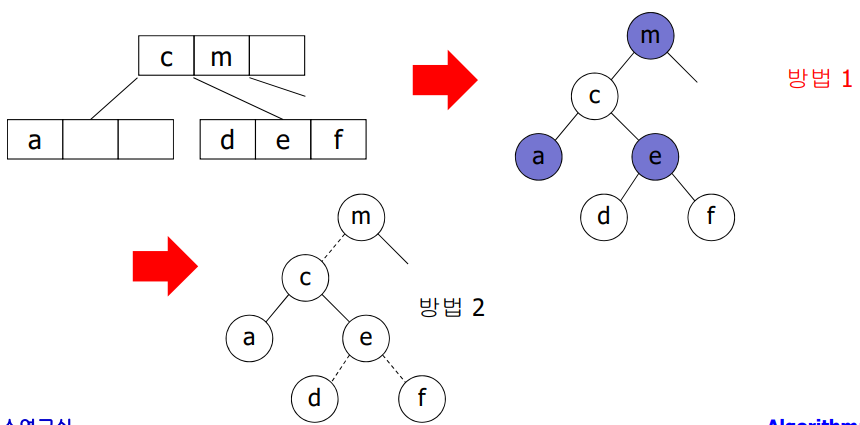
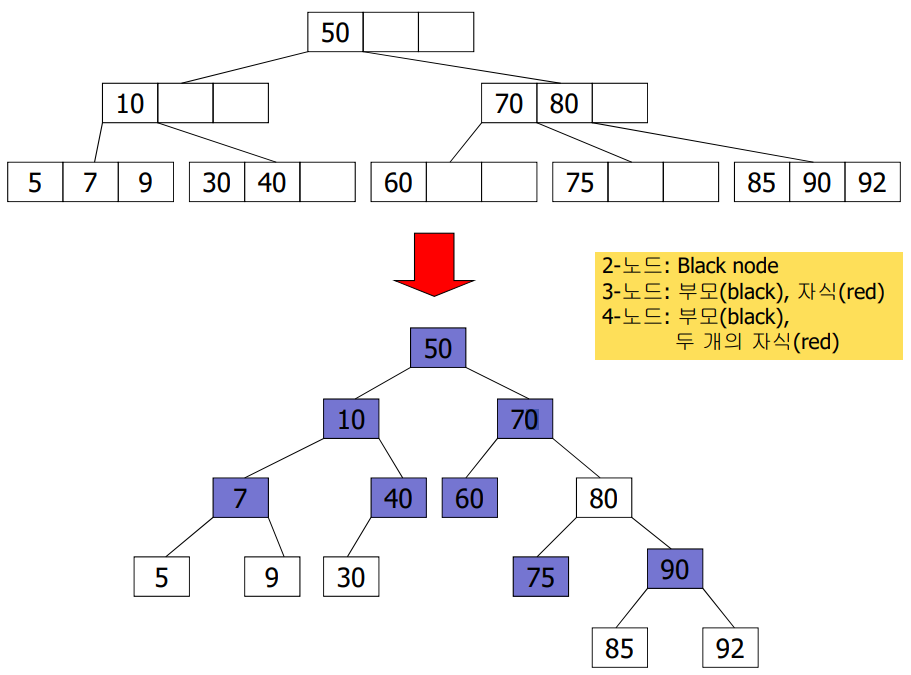
Red-Black Tree: 2-3-4 tree를 이진 트리로 표현
방법 1: 노드를 Black node와 Red node로 구분
방법 2: 링크를 Black link과 Red link로 구분

기본적인 성질
 Root property: 루트 노드는 black
 Red property: Red node의 자식 노드는 black
 부모-자식이 동시에 red node가 될 수 없음
 Depth property: 리프 노드에서 루트 노드까지의 모든 경로는 동일한 수의black node로 구성

n 개의 노드로 구성된 RB Tree의 높이 hRB = O(log n)
 n개의 노드를 갖는 2-3-4 트리의 높이: h234  log(n + 1)
 h234 <= hRB <= 2h234
 hRB <= 2log(n + 1)

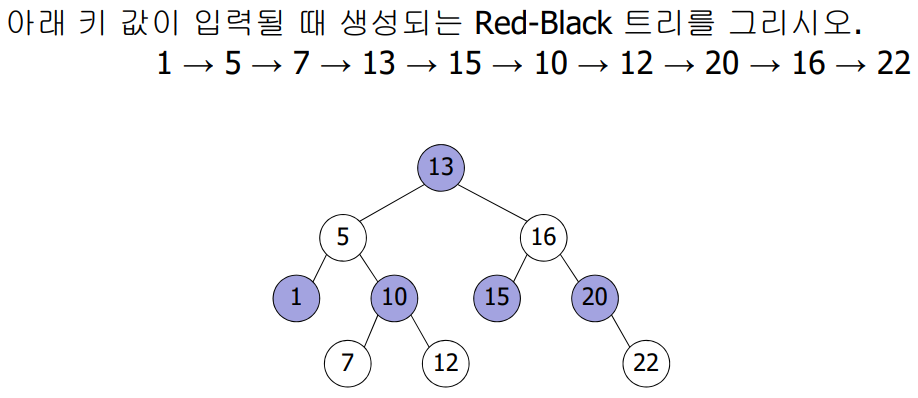
RB Tree의 연산

1. Searching
    일반적인 BST의 검색 방법을 이용하여 검색
    Node color는 사용되지 않음
2. Insertion
    BST의 삽입 과정과 유사
    노드 삽입 후 color 조정 (또는 회전) 필요
3. Deletion
    2-3-4 tree의 삭제 알고리즘을 red-black tree에 적용
4. RB Tree의 장점
    AVL Tree나 2-3-4 트리에 비해 트리 재구성의 빈도수가 낮음
    트리 재구성  Color 변경으로 대체 가능

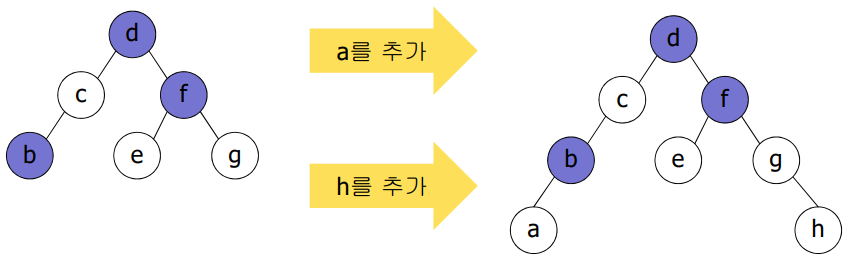
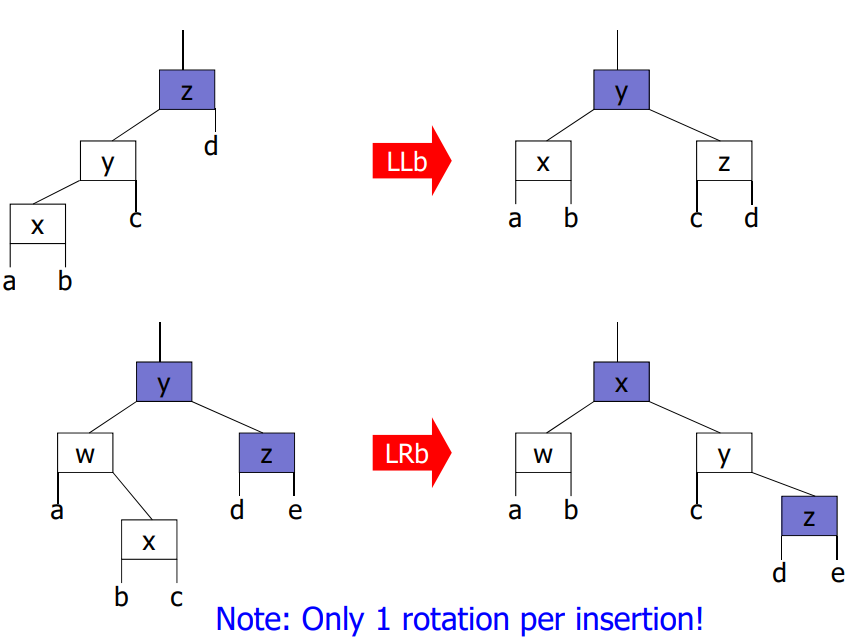
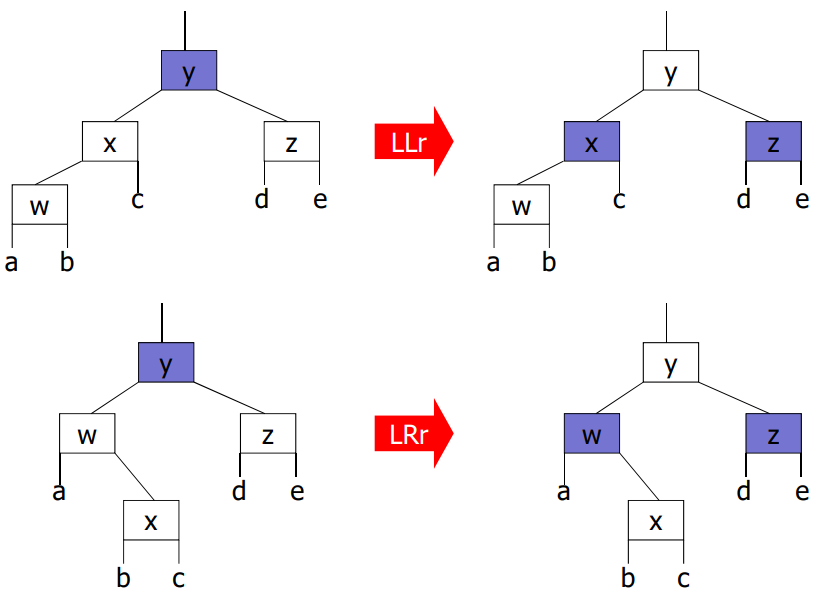
insertion 기본 규칙
 BST의 put() 알고리즘에 의해 추가할 노드 z의 위치 결정
 z가 루트이면, black
 z가 루트가 아니면, red
 z의 부모가 black일 경우에는 아무 문제 없음.
 z의 부모가 red일 경우, double red 문제 발생