1. Symbol Table이란?
1. Symbol Table 특성
- (키, 값) 쌍의 모임
특정 키와 그 키에 해당되는 값의 쌍을 삽입
키가 주어질 때, 관련된 값을 검색
2. Symbol Table의 예
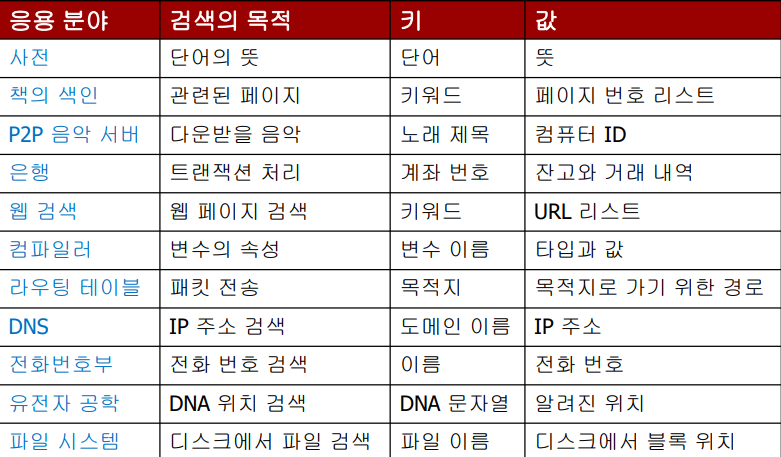
3. Symbol Table의 API
- 구현 1: 연결 리스트를 이용한 순차 검색
- 구현 2: 정렬된 배열을 이용한 이진 검색
- Ordered Symbol Table

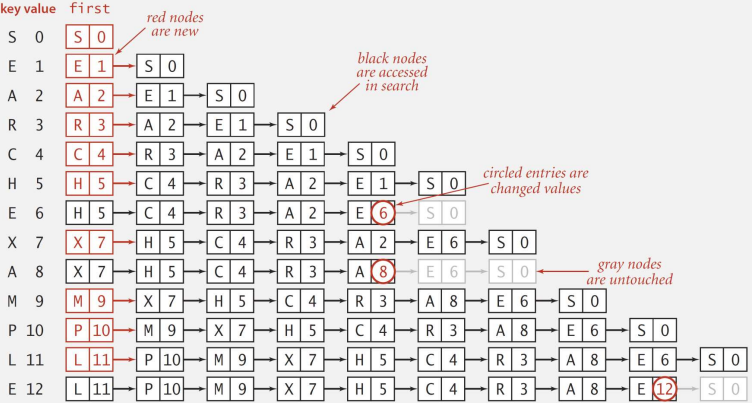
2. 연결 리스트를 이용한 순차 검색
(키, 값)의 쌍으로 구성된 연결 리스트를 유지
- 검색: 모든 키를 스캔하면서 입력 키와의 일치 여부 확인 -> 최대 O(n)
- 삽입: 모든 키를 스캔하면서 입력 키와의 일치 여부 확인, 일치하는 키가 없으면 리스트의제일 앞에 (키, 값)의 쌍을 추가 -> 최대 O(n)
class Node<K,V> { // 하나의 노드를 표현
// (키, 값, 다음 노드를 가리키는 참조)의 쌍으로 구성
K key; V value; Node<K,V> next;
public Node(K key, V value, Node<K,V> next) {
this.key = key; this.value = value; this.next = next;
}
}
public class SequentialSearchST<K,V> {
private Node<K,V> first; // 첫 번째 노드에 대한 참조를 유지. 초기값 = null
int N; // 연결 리스트의 노드 수를 유지. 초기값 = 0
public V get(K key) { 다음 슬라이드 참조 }
public void put(K key, V value) { 다음 슬라이드 참조 }
public void delete(K key) { 다음 슬라이드 참조 }
public Iterable<K> keys() { 다음 슬라이드 참조 }
public boolean contains(K key) { return get(key) != null; }
public boolean isEmpty() { return N == 0; }
public int size() { return N; }
}
public V get(K key) {
for (Node<K,V> x = first; x != null; x = x.next) // 연결 리스트를 스캔
if (key.equals(x.key))
return x.value; // search hit
return null; // search miss
}
public void put(K key, V value) {
for (Node<K,V> x = first; x != null; x = x.next)
if (key.equals(x.key)) { // 키가 있을 경우, 값만 변경
x.value = value;
return;
}
first = new Node<K,V>(key, value, first); // 키가 없으면, 앞에 노드 추가
N++;
}
public void delete(K key) {
if (key.equals(first.key)) { // 첫번째 노드를 삭제하는 경우
first = first.next; N--;
return;
}
for (Node<K,V> x = first; x.next != null; x = x.next) { // 삭제할 노드를 검색
if (key.equals(x.next.key)) {
x.next = x.next.next; N--;
return;
}
}
}
public Iterable<K> keys() {
ArrayList<K> keyList = new ArrayList<K>(N); // ArrayList는 Iterable을 구현
for (Node<K,V> x = first; x != null; x = x.next)
keyList.add(x.key);
return keyList;
}3. 정렬된 배열을 이용한 이진 검색
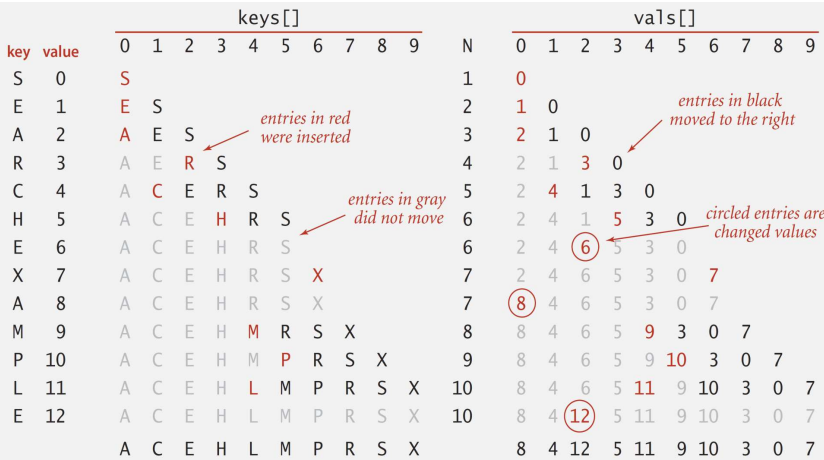
1. 키의 오름차순으로 (키,값)의 쌍을 배열에 저장
이유 : 정렬된 배열에서는 이진 검색이 가능
public class BinarySearchST<K extends Comparable<K>, V> {
private static final int INIT_CAPACITY = 10;
private K[] keys; // 키의 배열
private V[] vals; // 값의 배열 하나의 배열로 (키, 값) 쌍을 표현하는 방법?
private int N;
public BinarySearchST() {
keys = (K[]) new Comparable[INIT_CAPACITY];
vals = (V[]) new Object[INIT_CAPACITY];
}
public BinarySearchST(int capacity) {
keys = (K[]) new Comparable[capacity]; // 배열 용량보다 많은 키가 입력?
vals = (V[]) new Object[capacity];
}
public boolean contains(K key) {return get(key) != null; }
public boolean isEmpty() {return N == 0; }
public int size() { return N; }
}
private void resize(int capacity) { // 배열 크기를 동적으로 변경
K[] tempk = (K[]) new Comparable[capacity];
V[] tempv = (V[]) new Object[capacity];
for (int i = 0; i < N; i++) {
tempk[i] = keys[i];
tempv[i] = vals[i];
}
vals = tempv;
keys = tempk;
}
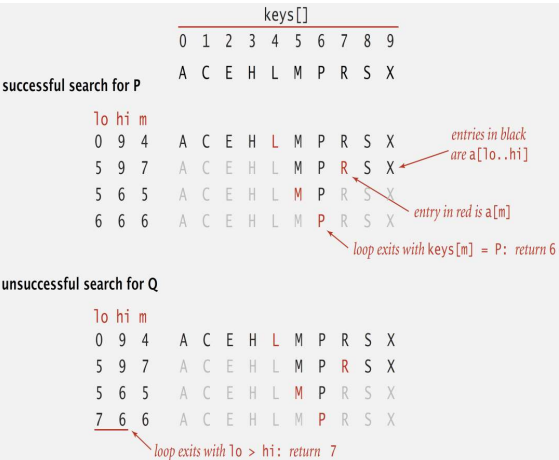
private int search(K key) { // 이진 검색
int lo = 0;
int hi = N – 1;
while (lo <= hi) {
int mid = (hi + lo) / 2;
int cmp = key.compareTo(keys[mid]);
if (cmp < 0) hi = mid – 1;
else if (cmp > 0) lo = mid + 1;
else return mid;
}
// 키가 없을 경우, -1이 아니라 lo가 반환
return lo;
}
public V get(K key) {
if (isEmpty()) return null;
int i = search(key); // 이진 검색
if (i < N && keys[i].compareTo(key) == 0)
return vals[i];
else return null; // 키가 없으면 null을 반환
}
public void put(K key, V value) {
int i = search(key); // 일단 키를 찾고…
if (i < N && keys[i].compareTo(key) == 0) // 있으면, 값만 변경. 왜 비교를 다시?
{ vals[i] = value; return; }
if (N == keys.length) // 없으면, 추가해야 하니 배열 크기 확장
resize(2 * keys.length);
for (int j = N; j > i; j--) {
keys[j] = keys[j-1]; vals[j] = vals[j-1];
} // 추가될 곳의 공간 확보
keys[i] = key; vals[i] = value; N++;
}
public void delete(K key) {
if (isEmpty()) return;
int i = search(key); // 이진 검색: 모든 키는 이진 검색으로 찾자!!!
if (i == N || keys[i].compareTo(key) != 0) return; // 없으면, 그냥 반환
for (int j = i; j < N-1; j++)
{
keys[j] = keys[j+1]; vals[j] = vals[j+1];
} // 뒤에 있는 키들을 한칸 앞으로. N--;
keys[N] = null; vals[N] = null; // 왜 null로 채울까?
if (N > INIT_CAPACITY && N == keys.length/4) // 배열이 너무 크면, 다시 줄이자. resize(keys.length/2);
}
public Iterable<K> keys() { // 연결 리스트의 경우와 거의 동일
ArrayList<K> keyList = new ArrayList<K>(N);
for (int i = 0; i < N; i++)
keyList.add(keys[i]);
return keyList;
}
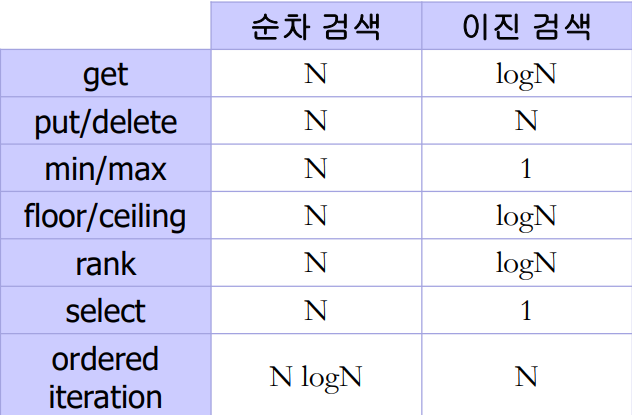
4. Ordered Operations
1. Ordered symbol table API

2. Ordered symbol table API의 예

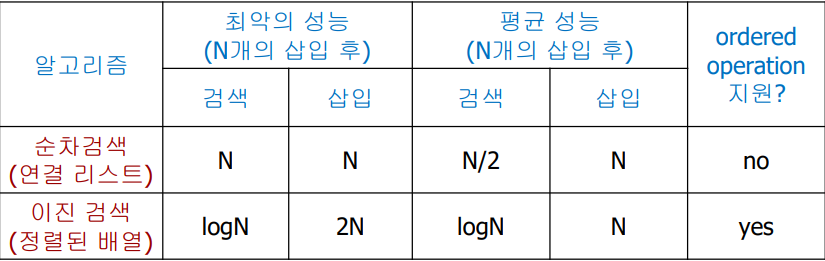
3. 순차 검색과 이진 검색의 성능