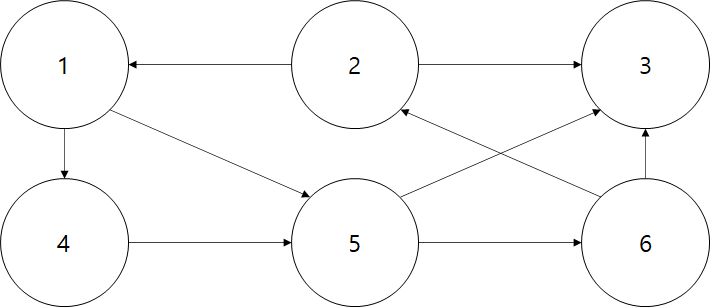
문제

그래프 1번 정점에서 각 정점으로 가는 최소 이동수를 구하세요.

코드

public class ShortGraphBFS {
    static int n,m = 0;
    static ArrayList<ArrayList<Integer>> graph;
    static int[] ch, dis;
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        m = sc.nextInt();
        graph = new ArrayList<>();
        for(int i=0; i<=n; i++){
            graph.add(new ArrayList<>());
        }
        ch = new int[n+1];
        dis = new int[n+1];
        for(int i=0; i<m; i++){
            int a = sc.nextInt();
            int b = sc.nextInt();
            graph.get(a).add(b);
        }
        ch[1] = 1;
        bfs(1);
        for (int i=1; i<=n; i++) {
            System.out.println(i+" = " +dis[i]);
        }
    }
    public static void bfs(int v){
        Queue<Integer> que = new LinkedList<>();
        ch[v] = 1;
        dis[v] = 0;
        que.offer(v);
        while(!que.isEmpty()){
            int cv = que.poll();
            for(int nv : graph.get(cv)){
                if(ch[nv] == 0){
                    ch[nv] = 1;
                    que.offer(nv);
                    dis[nv] = dis[cv] + 1;
                }
            }
        }
    }
}

설명

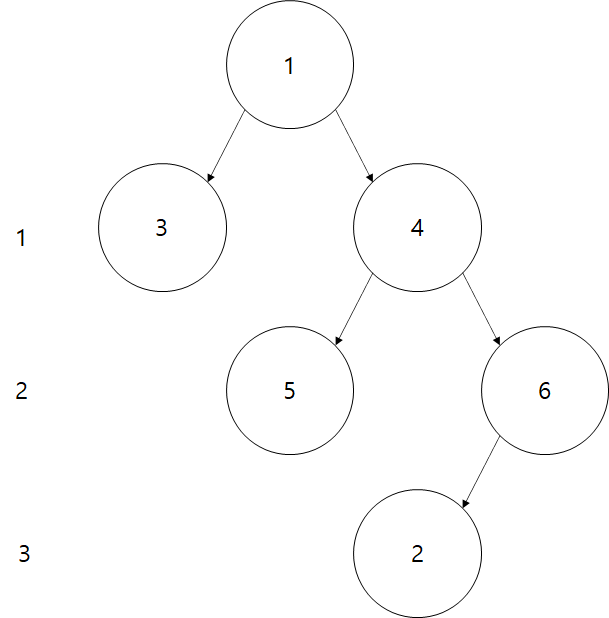
위 그래프를 1번 정점을 기준으로 이진 트리 구조로 변경하여 표현해보았다.

1번 정점에서 각 노드에 도달할 수 있는 단계를 표시한 것인데 이 단계가 즉 1번 정점에서 각 정점으로 도달할 수 있는 최소 거리가 된다.

이걸 다시 위의 코드와 동일하게 ArrayList로 표시하면

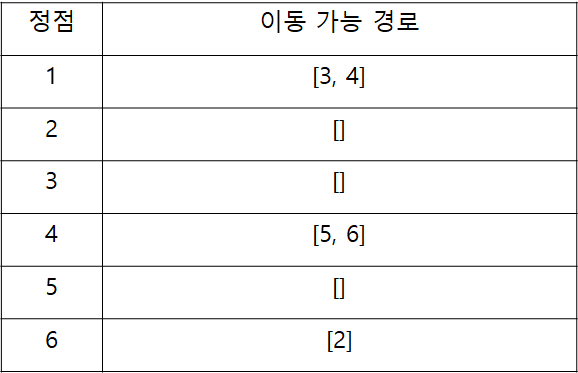
각 list의 이동 가능한 경로가 배열로 적혀지고 여기서 첫번째 정점에서 이동 가능한 3,4까지 최단 거리가 1이된다. 그리고 다시 각각 3과 4는 3에서는 이동할 수 있는 경로가 없어 종료되고 4의 경우 5,6이 존재하는데 5,6은 2번의 이동 후 도착할 수 있는 지점이 되고 5는 경로가 없어 종료, 6은 2로 이동하여 최종 2는 3번째에 도착할 수 있는 정점이된다.

아직 코드 자체로 이해하기엔 어렵다...ㅜㅜ 이제부터 개념문제는 끝나고 실제 문제 풀이로 들어가니 문제를 풀어보면서 감을 잡아보자!!!