
실수 자료형을 사용하면서 항상 실수 자료형은 근사값이거나 정확하지 않기때문에 주의해야한다는 이야기를 듣곤합니다. 오늘 그 이유에 대해서 파헤쳐 보도록 하겠습니다.
1. 이진수로 실수를 표현하는 법
컴퓨터는 이진수로 이루어진 명령어만 이해하기 때문에 실수 또한 2진수로 변경이 가능해야합니다. 실수는 정수부와 소수부로 이루어져있으며, 이 둘은 2진수로 변환하는 방식이 서로 다릅니다.
먼저, 정수부의 경우 해당 값이 몇개의 2의 거듭 제곱으로 이루어져있나 를 확인하는 과정이기 때문에 2를 나눠주며 나머지를 활용해 2진수를 구합니다.
소수부의 경우 정수부와 반대로 2의 음수 제곱을 얼마나 포함하는가를 확인하는 과정이기 때문에 2를 곱해주며 오버플로우가 나는 것을 활용해 2진수를 구하게 됩니다.
그럼 그 과정을 예시를 들어 보여드리겠습니다.
11.765625
- 정수부: 11
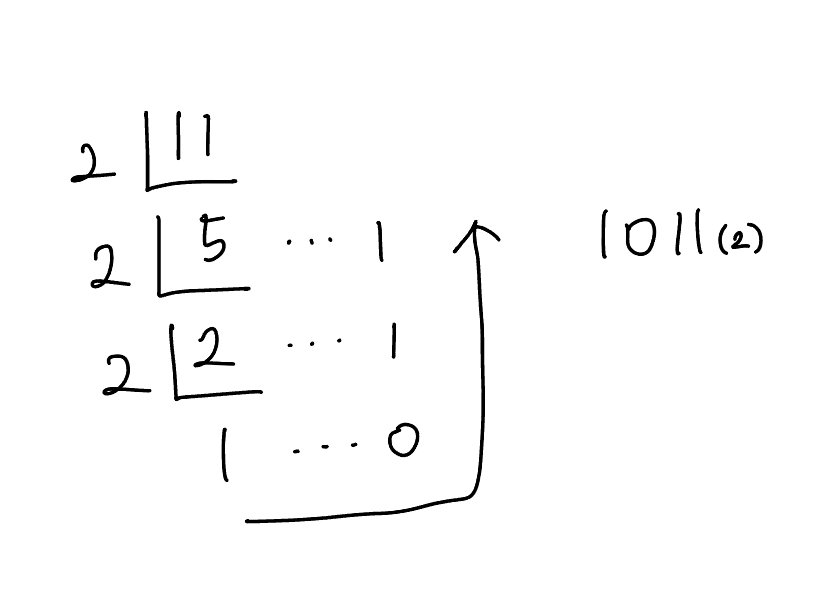
- 소수부: 0.765625
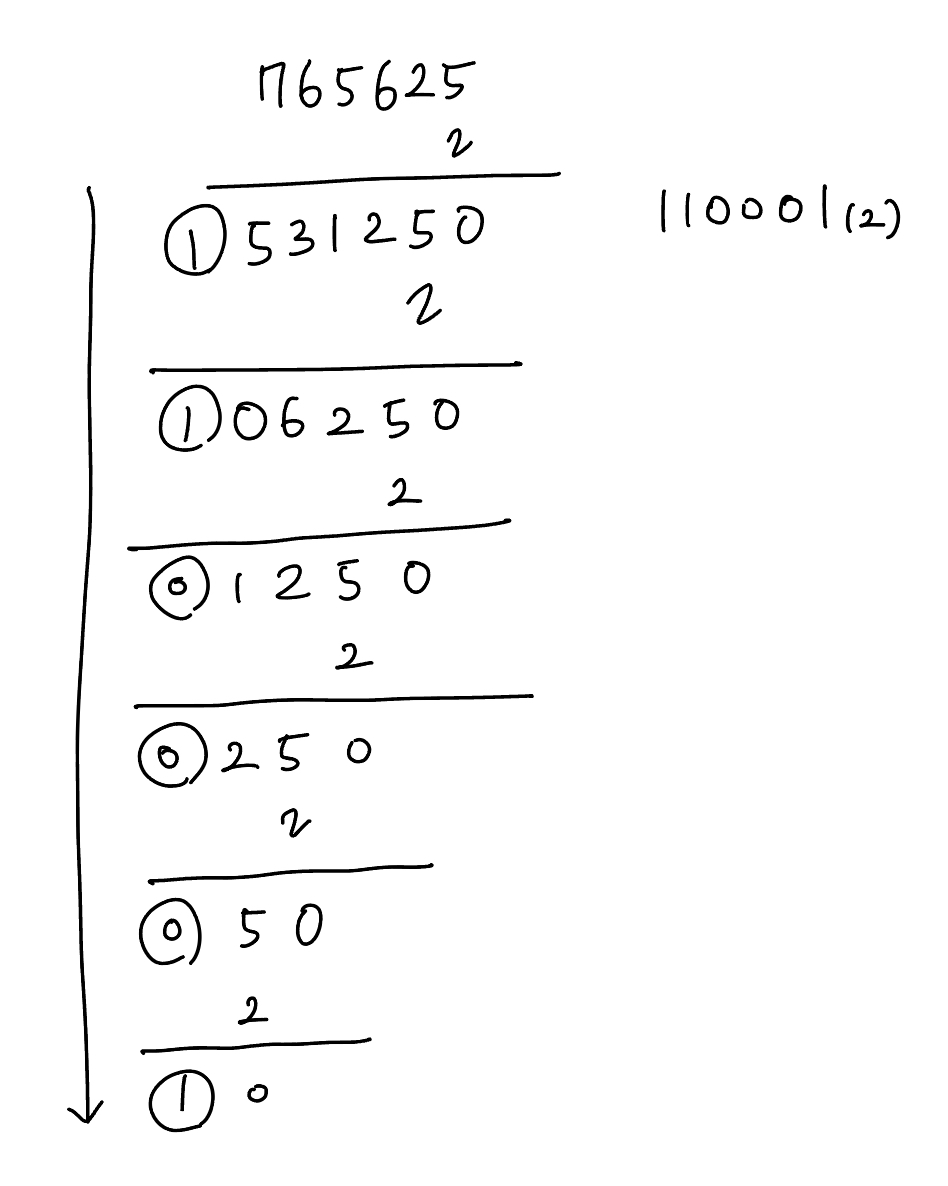
위 과정을 통해 정수부와 소수부의 이진수 변환이 이루어졌고, 둘을 합쳐줌으로써
11.765625 라는 10진수 표현식은 1011.110001(2) 이라는 2진수로 표현될 수 있다는 것을 확인할 수 있습니다.
2. 무한 소수
실수에는 일정 패턴이 반복되거나 같은 수가 무한히 반복되는 ‘무한소수’라는 개념도 있습니다. 하지만, 컴퓨터 메모리의 특성상 무한한 수를 저장할 수는 없기 때문에 10진수의 소수를 2진수로 변환할 때 많은 경우 정확한 변환이 불가능합니다.
0.1의 경우 2진수로 변환했을때 무한히 반복되는 것을 확인할 수 있습니다.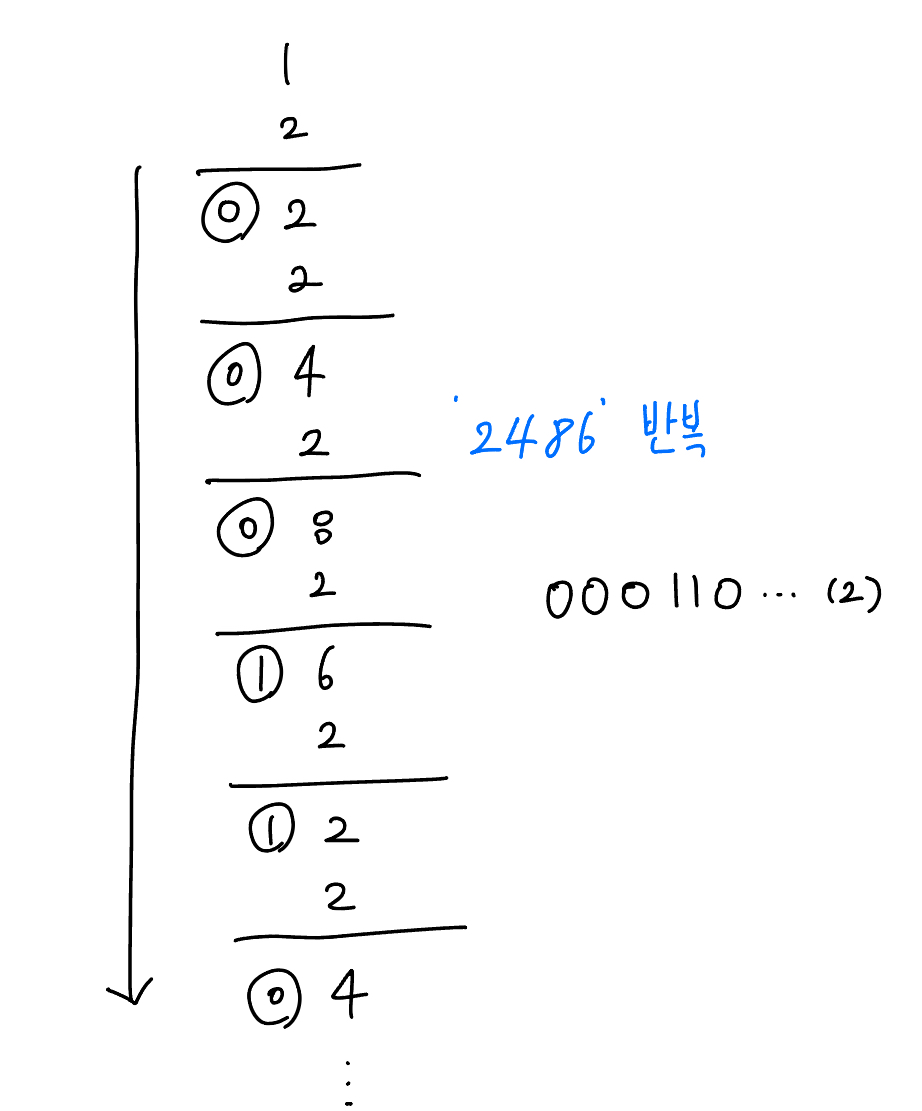
→ 대다수의 수는 정확하게 2진수로 변환이 어려우며 소수의 끝이 5가 아닌 수를 2진수로 표현할 경우 무한 소수가 발생한다고 볼 수 있습니다.
3. 실수의 메모리 표현
지금까지 10진수의 실수를 2진수로 변환하는 방법에 대해 알아보았습니다.
변환된 2진수 실수는 컴퓨터 메모리에 저장될 때 고정소수점 방식, 부동소수점 방식 중 하나로 저장됩니다.
고정 소수점 방식(Fixed-Point Number Representation)
고정 소수점 방식은 소수점 자릿수가 고정된다는 의미로 실수를 정수부와 소수부로 나누어 저장하는 방식을 말합니다.
32bit 기준으로 보았을때 부호(1bit) + 정수부(15bit) + 실수부(16bit)로 구성됩니다.

| 장단점 | 특징 |
|---|---|
| 장점 | 정수부와 소수부를 나누어 저장하기 때문에 직관적입니다. |
| 단점 | 정수부 15 bit, 소수부 16 bit로 고정되어있기 때문에 표현 가능한 범위가 매우 적습니다. |
| 고정된 자릿값으로 인해 낭비되는 메모리가 존재합니다. | |
| 정밀도가 낮습니다. |
부동 수수점 방식(Fixed-Point Number Representation)
부동 소수점 방식은 소수점의 위치가 정해져 있지 않았다는 의미에서, 숫자를 가수부와 지수부로 나누어 표현하는 방식입니다.
32bit 기준으로 보았을때 부호(1bit) + 지수부(8bit) + 가수부(23bit)로 구성됩니다.

지수부는 소수점의 위치(크기)를 결정하는 역할을 하며, 가수부는 실제 숫자의 유효 자릿수를 나타냅니다.(가수부는 1.xxx 형태로 표현되며 해당 소수점을 기준으로 지수부가 결정됩니다.)
| 장단점 | 특징 |
|---|---|
| 장점 | 정수, 소수가 나누어져있지 않아 큰 범위의 값을 표현할 수 있습니다. |
| 정수, 소수의 크기에 상관없이 가수부 내 전체 실수를 표현하기 때문에 메모리 낭비 문제가 없습니다. | |
| 단점 | 항상 오차가 존재합니다. |
-
부동 소수점 계산 방법(정규화)
부동 소수점 방식은 IEEE 754 표준을 따르며 수식은 다음과 같습니다.
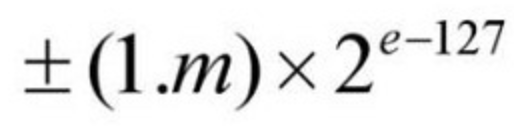
m은 가수부를, e는 지수부를 의미합니다.
부동소수점 방식은 실수를 저장할 때, 변환된 2진수를 지수 표현식 형태로 바꾸는
정규화(Normalization)과정을 거친 후, 그 결과를 부호 비트, 지수부, 가수부로 나누어 메모리에 저장합니다.-118.625 를 부동소수점 방식으로 변경해보겠습니다.
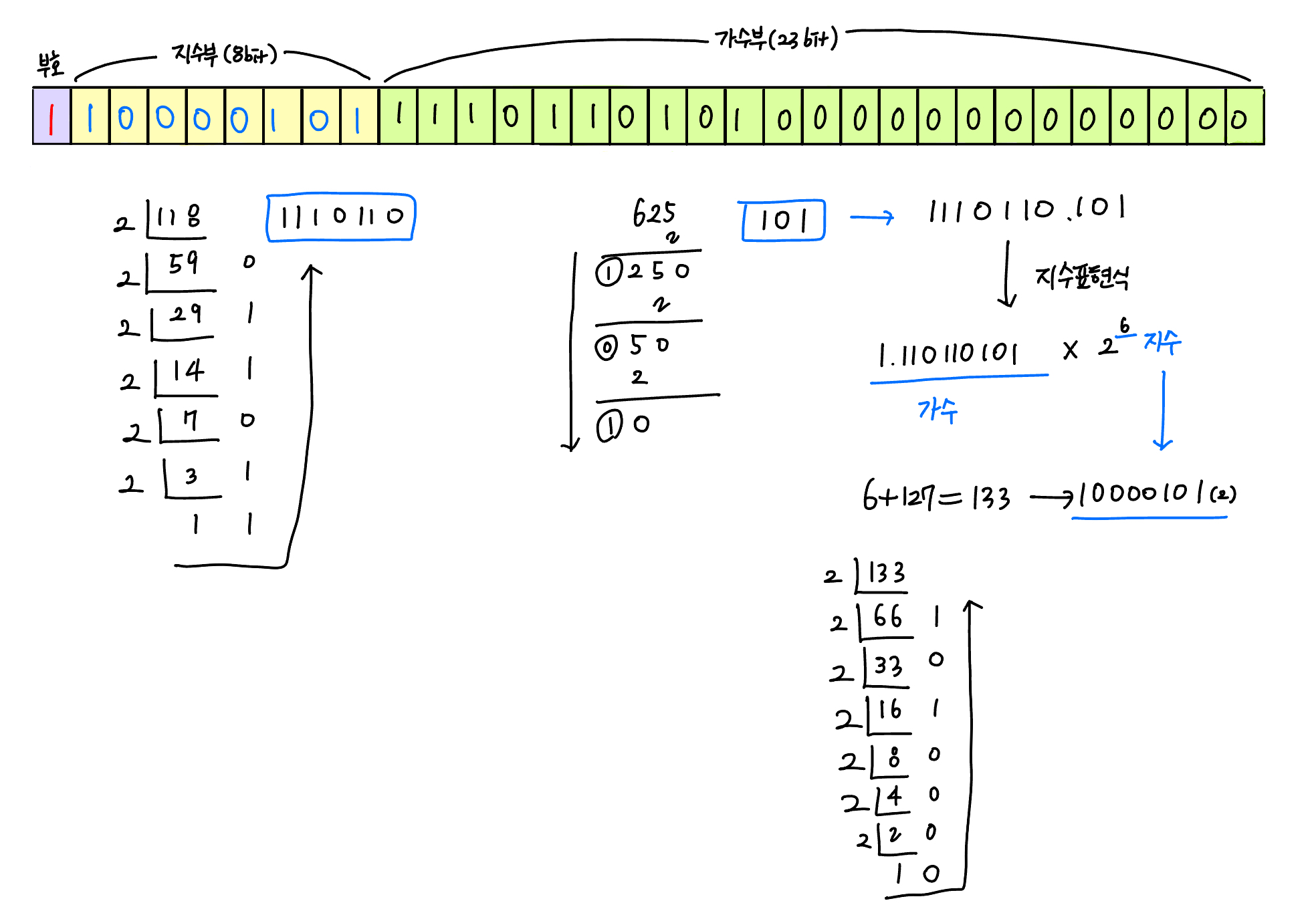
이때, 지수부에는 고정된 값인
bias(127)을 더해 저장하게 되는데, 이것은 지수가 음수가 될 수 있는 경우를 고려한 설계입니다.127이라는 bias 값을 더해줌으로써 0~127은 음수를, 128~255는 양수를 표현할 수 있게 됩니다.
3. 소수의 계산 오차
앞서 언급했듯이, 소수의 끝자리가 5로 끝나지 않거나 무한히 반복되는 경우, 컴퓨터는 표현 가능한 비트수의 한계로 모든 자릿수를 정확히 저장할 수 없습니다.
이로 인해 마지막 자릿수에 반올림이 발생하고, 결과적으로 부정확한 실수 값이 저장되게 됩니다.
10진수를 2진수로 변환하는 과정 자체는 고정소수점과 부동소수점 모두 동일하기 때문에 두가지 방식 모두 오차가 발생하는 근본적 원인은 같습니다.
그렇다면 왜? 부동소수점이 고정소수점보다 더 부정확하다는 말이 나오는걸까요?
부동소수점은 가수부와 지수부로 나뉘며, 소수점의 위치가 고정되지않은 방식이라는 것을 앞서 살펴보았습니다. 하지만, 가수부는 23 Bit 내에 전체 수를 저장해야하기 때문에 값이 커질수록 정수부에 비해 비교적 크기가 작은 소수부의 경우 반올림 과정을 통해 표현하게 됩니다.
이것은 넓은 수의 범위를 표현하기위해 정밀도를 희생한 구조이기 때문입니다.
부동소수점은 1.x * 2^e 형태로 e(지수부)가 커질수록 소수점은 오른쪽으로 이동하게 됩니다.
이 경우, 가수부의 비트가 정수부 표현에 더 많이 사용되게 되면서, 소수부에서 사용할 수 있는 비트수가 줄어들게되고 결과적으로 정밀도가 떨어지게 됩니다.
반대로, 고정소수점은 소수점의 위치가 고정되어있기 때문에, 값이 커지더라도 정수부와 소수부에 배정된 비트수는 변하지 않습니다. 즉, 고정소수점 방식은 값이 커지더라도 소수부의 정밀도는 동일하기 때문에 값이 커질수록 부동소수점보다 값이 정확하다는 말이 나오는 것입니다
실수? 이제 알고 사용하자구요~
