1504. Count Submatrices With All Ones

문제

Given an m x n binary matrix mat, return the number of submatrices that have all ones.

• m x n 이진 매트릭스가 주어질때
• 모든 1로만 이루어진 서브매트릭스의 갯수를 구하라
• Ex. 1x1, 2x1 등등

예시

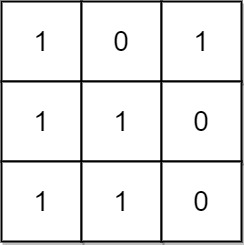
• 13개 있음
  • 1x1 6개
  • 1x2 2개
  • 2x1 3개
  • 2x2 1개
  • 3x1 1개

제한

• $1 <= m, n <= 150$
• 매트릭스는 0과 1로만 이루어져 있음

풀이

1. 자신을 기준으로 하여 왼쪽에 1이 총 몇개가 있는지 구하는 matrix를 하나 만든다.
   • 다만 자신이 0일경우 0으로 채운다.
2. 해당 matrix를 루프를 돌아서, 자신으로부터 위로 탐색해 비교해가면서, 최소값을 갱신해가며 ans에 더한다.
   • 해당 값이 그 점이 오른쪽 아래에 해당할때 만들수 있는 모든 직사각형의 갯수

class Solution:
    def numSubmat(self, mat: List[List[int]]) -> int:

        ROW = len(mat)
        COL = len(mat[0])

        dp = [
            [0] * COL for _ in range(ROW)
        ]

        for r in range(ROW):
            cnt = 0
            for c in range(COL):
                if mat[r][c]:
                    cnt += 1
                else:
                    cnt = 0

                dp[r][c] = cnt

        ans = 0

        for r in range(ROW):
            for c in range(COL):
                minima = dp[r][c]
                for tr in range(r, -1, -1):
                    if dp[tr][c] > 0:
                        minima = min(minima, dp[tr][c])
                        ans += minima
                    else:
                        break

        return ans

• O(N^3) 이지만, N이 150이라 400만정도로 안정적으로 동작한다.