Leetcode 102. Binary Tree Level Order Traversal with Python - 리뷰 O

문제

Given the root of a binary tree, 
return the level order traversal of its nodes' values. (i.e., from left to right, level by level).

이진 트리 root에 대해 level order traversal을 실행하고 그 값을 이차원 배열로 리턴하시오.

예시

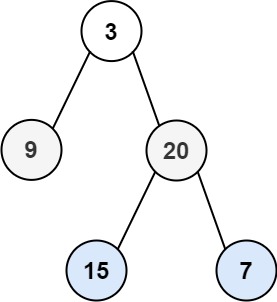
Input: root = [3,9,20,null,null,15,7]
Output: [[3],[9,20],[15,7]]

리턴 트리의 index는 tree 내에서의 node의 레벨을 의미 한다.

제한

• 노드 값의 범위는 [0, 2000].
• 1000 <= Node.val <= 1000

풀이법

기본적으로 Node는

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
        

위와 같은 자료형을 사용하는데, 본 문제를 해결하기 위해선 노드의 레벨을 저장할 필요가 있기에

class LevelNode:
    def __init__(self, node: TreeNode, level: int):
        self.node = node
        self.level = level
    

위와 같은 클래스를 하나 더 선언하였습니다.

이후 큐를 이용해 bfs search를 돌리면서 레벨을 기록해 dictionary에 저장하였고

저장된 dictionary를 2차원 배열로 변환해 리턴하였습니다.

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class LevelNode:
    def __init__(self, node: TreeNode, level: int):
        self.node = node
        self.level = level

class Solution:
    def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
        if root == None: return []

        // 루트 노드를 집어 넣고 시작
        q = [ LevelNode(root, 0) ]

        ans = dict()

        while len(q) != 0:
            node = q[0]
            q.pop(0)
            if node.level not in ans:
                ans[node.level] = list()
            ans[node.level].append(node.node.val)
            if node.node.left != None:
                // 자식 노드는 레벨 1 증가
                q.append(LevelNode(node.node.left, node.level + 1))
            if node.node.right != None:
                q.append(LevelNode(node.node.right, node.level + 1))

        ret = []
        for i in range(10000):
            if i not in ans: break
            ret.append(ans[i])

        return ret
        

n개의 노드를 순환할때 시간 복잡도는 O(n) 입니다.

( 2024 / 12 / 05 )

복기

• 조금 더 효율적이고 간략한 접근법

class Solution:
    def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
        if root is None:
            return []

        ans = []
        q = deque([root])

        while q:
            current_level = []
            level_size = len(q)

            for _ in range(level_size):
                node = q.popleft()
                current_level.append(node.val)

                if node.left:
                    q.append(node.left)
                if node.right:
                    q.append(node.right)

            ans.append(current_level)

        return ans