Leetcode 1063. Numbers of Valid Subarrays

문제

Given an integer array nums, 
return the number of non-empty subarrays with the leftmost element of the subarray 
not larger than other elements in the subarray.

A subarray is a contiguous part of an array.

• 정수 배열 nums가 주어진다.
• nums의 부분배열중 가장 왼쪽의 값이 부분배열의 최솟값이 되는 모든 부분 배열의 갯수를 구하라.
• 예시
  • [2, 4, 3] - 2가 제일 작기에 유효하다.
  • [3, 1, 2] - 3이 배열에서 제일 작은 수가 아니기에 유효하지 않다.

예시

nums = [1, 4, 2, 5, 3]
정답 : 11
이유 : [1],[4],[2],[5],[3],[1,4],[2,5],[1,4,2],[2,5,3],[1,4,2,5],[1,4,2,5,3] 가 유효한 부분배열이다.

제한

• $1 <= nums.length <= 5 * 10^4$
• $0 <= nums[i] <= 10^5$

풀이법

• monotonic stack을 이용한다
• nums가 [14,20,5,13,18,8,2,14,3,13] 인 경우를 예시로 든다.

MONOTONIC STACK

• (인덱스, 값) 을 원소로 가진다.
• 값이 점차 증가하게 한다.
• 즉, 처음부터 끝까지 숫자에 대해 stack을 만들면 여기에 있는 숫자는 반드시 자신을 포함한 맨 오른쪽까지 배열에서 가장 작은 숫자가 된다.

• 14가 stack에 들어온다.

• 20이 stack에 들어온다.

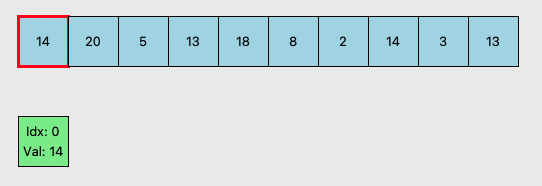
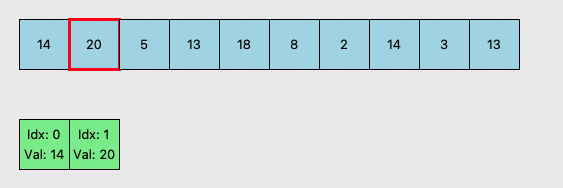
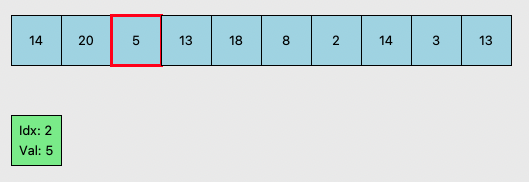
• 5가 stack에 들어오려 하는데 이러면 14, 20, 5로 stack이 더이상 오름차순이 아니게 된다.
  • stack이 비거나 오름차순이 될때까지 숫자를 pop 한다.
  • 이때 현재 index - pop된 index 는 스택 내부 숫자로부터 시작해 만들수 있는 올바른 부분배열의 갯수이기에 이를 정답에 더한다.
  • EX. 20은 [20] 하나가 가능 -> 2 - 1
  • EX. 14는 [14], [14, 20] 두개가 가능 -> 2 - 0

class Solution:
    def validSubarrays(self, nums: List[int]) -> int:
        a = []

        N = len(nums)

        ans = 0
		
        for i, n in enumerate(nums):
        	# 오름차순이 되지 않을시 제거 및 정답에 더함
            while a and a[-1][1] > n:
                p = a.pop()
                ans += i - p[0]
            a.append((i, n))

		# 만들수 있는 나머지 경우를 더한다.
        for i, _ in a:
            ans += N - i

        return ans