Leetcode 11. Container With Most Water with Python - 리뷰 O

본 문서는 https://www.udemy.com/course/master-the-coding-interview-big-tech-faang-interviews/ 강의를 참조하여 작성되었습니다.

문제

You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]).

Find two lines that together with the x-axis form a container, such that the container contains the most water.

Return the maximum amount of water a container can store.

Notice that you may not slant the container.

길이가 n인 높이의 배열 height가 주어집니다.
n개의 수직선이 그어진다고 할때,
두 선을 이용해 물을 가둔다고 생각하고 가둘수 있는 물의 최대 너비를 구하시오.

예시

Input: height = [1,8,6,2,5,4,8,3,7]
Output: 49
Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.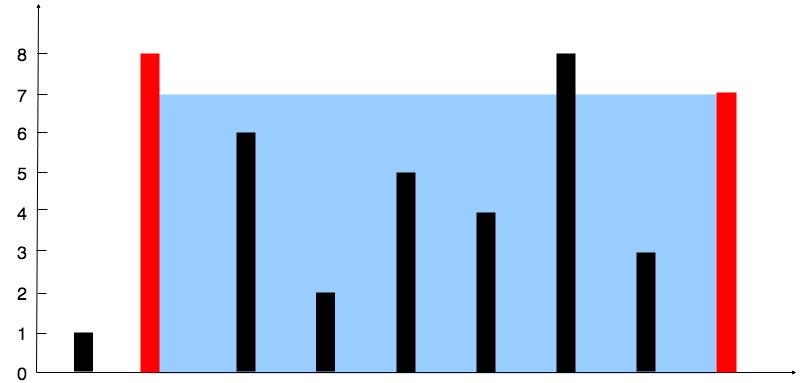

제한

• n == height.length
• 2 <= n <= 105
• 0 <= height[i] <= 104

풀이법

풀이에 앞서

두 선 사이의 너비는 두선중 작은선의 길이 * 인덱스의 차이 이다.

python code로는 min(height[a], height[b]) * (b-a)

1. BRUTE FORCE

모든 가능한 경우의 수를 전부 확인한다.

시간복잡도는 O(n^2)이고 공간복잡도는 O(1)이다.

def water(heights):
    max = -1
    for i in range(len(heights)):
        for j in range(i+1, len(heights)):
            square = min(heights[i], heights[j]) * (j - i)
            if max < square:
                max = square
    return max
 

2. SHIFTING POINTER

두 선 사이의 너비가 넓어지려면 중요한것이 두가지 있다.

1. 두 선 사이의 인덱스 차이가 많이 나야 한다.
2. 두 선 중 작은값이 최대한 커야한다.

이 둘을 만족하는것을 찾기위해 두 선을 찾되 맨 왼쪽과 맨 오른쪽 두 선부터 찾아 나가는 것이다.

맨 왼쪽과 맨 오른쪽의 두 선이라면 밑면, 즉 인덱스의 차이가 가장 클것이다.

이 경우부터 너비를 구해 최댓값이였는지 확인 한 후, 두 선중 작은 값에 대해서만 안쪽으로 한칸 움직인다.

그럴 경우 두선의 길이중 최솟값이 갱신되기에, 길이가 줄더라도 기존의 최댓값이 유지되며, 길이가 길면 최댓값이 갱신될 것이다.

이를 두 선이 겹칠때까지 반복하는 것이다.

def water(heights):
    a = 0
    b = len(heights)-1
    maximal = -1

    # 두 선이 겹치기 직전까지
    while a != b:
        # 현재 두 선의 너비를 계산 한 후 최댓값을 갱신한다.
        space = min(heights[a], heights[b]) * (b - a)
        if maximal < space:
            maximal = space

        # 최솟값이 위치하는 쪽을 안쪽으로 한칸 보낸다.
        if heights[a] < heights[b]:
            a += 1
        else:
            b -= 1
    return maximal

이 경우 시간복잡도는 O(n), 공간복잡도는 따로 자료구조를 사용하지 않았기에 O(1)이 된다.

공간복잡도를 키우지 않고 시간복잡도를 극적으로 줄일수 있었다.

(2024 / 11 / 19)

복기

• 딱 보니까 투 포인터를 쓸것 같이 생기긴 했다
• 다만 모노토닉 스택을 써도 될 것 같아서 시도는 해봄..

class Solution:
    def maxArea(self, height: List[int]) -> int:
        res,cur,p = 0,0,max(height)
        l,r = 0, len(height) - 1
        while l<r:
            cur = (r-l) * min(height[l], height[r])
            if cur>res: res=cur
            elif height[r]>height[l]: l+=1
            else: r-=1
            if (r-l) * p < res: break
        return res