Leetcode 1466. Reorder Routes to Make All Paths Lead to the City Zero

There are n cities numbered from 0 to n - 1 and n - 1 roads 
such that there is only one way to travel between two different cities (this network form a tree). 
Last year, The ministry of transport decided to orient the roads in one direction 
because they are too narrow.

Roads are represented by connections where connections[i] = [ai, bi] represents a road from city ai to city bi.

This year, there will be a big event in the capital (city 0), 
and many people want to travel to this city.

Your task consists of reorienting some roads such that each city can visit the city 0. 
Return the minimum number of edges changed.

It's guaranteed that each city can reach city 0 after reorder.

0 ~n-1 으로 이름붙혀진 n개의 도시와 그 도시들을 잇는 도로 n-1 개의 배열이 주어진다.
두 도시를 건너는 방법은 하나밖에 없다. ( 사이클이 없다 )
connections[i] 배열의 [a_i, b_i] 는 a도시에서 b도시로 가는 도로가 존재한다는 의미이다.
0번 도시로 모든 도시가 이동할수 있게 도로의 방향을 바꿀때, 최소한으로 바꾸려면 얼마나 바꿔야 하는가?

예시

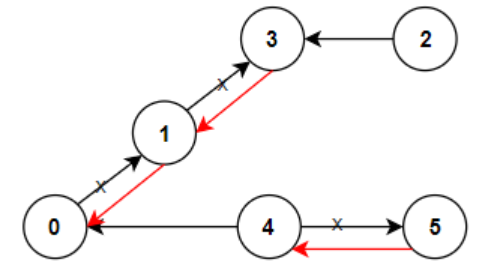
Input: n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
Output: 3
Explanation: 그림에 주어진 edge의 방향을 바꾼다.

풀이

1. 일단 cycle이 존재하지 않고 n개의 node와 n-1개의 edge가 존재하기에, 전체적인 모양이 트리 모양을 할 것임을 알수 있다.
   제일 중요!!

2. 먼저 연결된 도로를 set 자료구조에 (출발지점, 도착지점) 으로 모두 저장한다.

3. node n에 연결된 모든 이웃 node를 Hashmap으로 저장한다.

4. 그 후 아래와 같이 dfs를 한다.

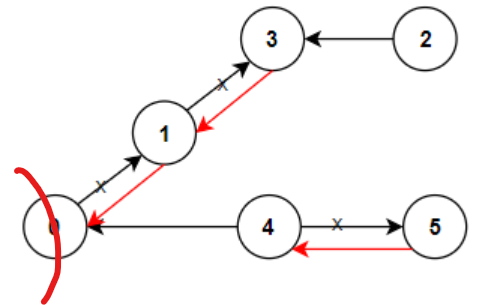
• 0에서 연결된 이웃은 1, 4가 있다.
• 근데 1 -> 0 로 가는 도로는 존재하지 않기에 이는 이웃하나 방향이 반대라는것을 알수있다.
  • 즉, 변경해야 하는 도로 수를 1 늘린다.
• 4 -> 0으로 가는 도로는 존재하기에 그대로 진행한다.
• 여기서 한번 검사한 도로는 check 배열을 통해 관리하고 dfs를 재귀적으로 실행한다.

from typing import Dict

class Solution:
    def minReorder(self, n: int, connections: List[List[int]]) -> int:
        edges = { (src, dst) for src, dst in connections }
        check = [ False for _ in range(n) ]
        count = 0
        neighbor: Dict[int, List[int]] = { city: [] for city in range(n) }

        check[0] = True

        for src, dst in connections:
            neighbor[src].append(dst)
            neighbor[dst].append(src)

        def dfs(city: int):

            nonlocal edges, check, count, neighbor

            for n in neighbor[city]:
                if check[n]:
                    continue
                else:
                    check[n] = True
                    if (n, city) not in edges:
                        count += 1
                    dfs(n)

        dfs(0)

        return count