Leetcode 1976. Number of Ways to Arrive at Destination

문제

You are in a city that consists of n intersections numbered from 0 to n - 1 with bi-directional roads between some intersections. The inputs are generated such that you can reach any intersection from any other intersection and that there is at most one road between any two intersections.

You are given an integer n and a 2D integer array roads where roads[i] = [ui, vi, timei] means that there is a road between intersections ui and vi that takes timei minutes to travel. You want to know in how many ways you can travel from intersection 0 to intersection n - 1 in the shortest amount of time.

Return the number of ways you can arrive at your destination in the shortest amount of time. Since the answer may be large, return it modulo 109 + 7.

• 0 ~ n-1 노드로 이루어진 무방향 그래프가 있습니다.
• 0에서 n-1노드까지 가는 경로 중 가장 구성하는 weight의 길이의 합이 짧은것들의 갯수를 구하세요
• 다만 숫자가 너무 크면 10^9 + 7 을 더하세요

---

예시

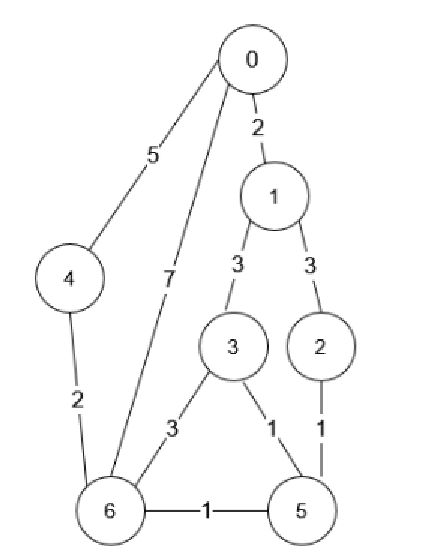
입력:
n = 7, roads = [[0,6,7],[0,1,2],[1,2,3],[1,3,3],[6,3,3],[3,5,1],[6,5,1],[2,5,1],[0,4,5],[4,6,2]]

출력:
4

설명:
교차로 0번에서 6번까지 이동하는 데 걸리는 최소 시간은 7분입니다.
7분 안에 도달할 수 있는 방법은 다음 네 가지입니다:

• 0 → 6
• 0 → 4 → 6
• 0 → 1 → 2 → 5 → 6
• 0 → 1 → 3 → 5 → 6

---

제한

• $1 <= n <= 200$
• $n - 1 <= roads.length <= n * (n - 1) / 2$
• roads[i].length == 3
• $0 <= u_i, v_i <= n - 1$
  $1 <= timei <= 10^9$
  $u_i != v_i$
• 두 정점을 잇는 간선은 최대 하나가 있다.
• 모든 정점은 연결되어 있다.

---

풀이

• 다익스트라로 풀되, 자신의 정점에 해당하는 최소 거리가 짧은 갯수를 계속 count 해야 한다.

class Solution:
    def countPaths(self, n: int, roads: List[List[int]]) -> int:
        distances = [float('inf')] * n
        count = [0] * n
        count[0] = 1

        q = [(0, 0)]
        graph = defaultdict(list)

        MOD = 10 ** 9 + 7

        for a, b, w in roads:
            graph[a].append((b, w))
            graph[b].append((a, w))

        while q:
            distance, node = heappop(q)

            for to, weight in graph[node]:
                if weight + distance < distances[to]:
                    distances[to] = weight + distance
                    count[to] = count[node]
                    heappush(q, (weight + distance, to))
                elif weight + distance == distances[to]:
                    count[to] = (count[to] + count[node]) % MOD
                   

        return count[-1]