Leetcode 2463. Minimum Total Distance Traveled

문제

There are some robots and factories on the X-axis. You are given an integer array robot where robot[i] is the position of the ith robot. You are also given a 2D integer array factory where factory[j] = [positionj, limitj] indicates that positionj is the position of the jth factory and that the jth factory can repair at most limitj robots.

The positions of each robot are unique. The positions of each factory are also unique. Note that a robot can be in the same position as a factory initially.

All the robots are initially broken; they keep moving in one direction. The direction could be the negative or the positive direction of the X-axis. When a robot reaches a factory that did not reach its limit, the factory repairs the robot, and it stops moving.

At any moment, you can set the initial direction of moving for some robot. Your target is to minimize the total distance traveled by all the robots.

Return the minimum total distance traveled by all the robots. The test cases are generated such that all the robots can be repaired.

Note that

All robots move at the same speed.
If two robots move in the same direction, they will never collide.
If two robots move in opposite directions and they meet at some point, they do not collide. They cross each other.
If a robot passes by a factory that reached its limits, it crosses it as if it does not exist.
If the robot moved from a position x to a position y, the distance it moved is |y - x|.

• 고장난 로봇과 특정한 갯수의 로봇만을 고칠수 있는 공장이 있다.
• 로봇이 최소한으로 이동하여 전부 고쳐질때, 이동한 거리를 구하시오.

예시

robot = [0,4,6], factory = [[2,2],[6,2]]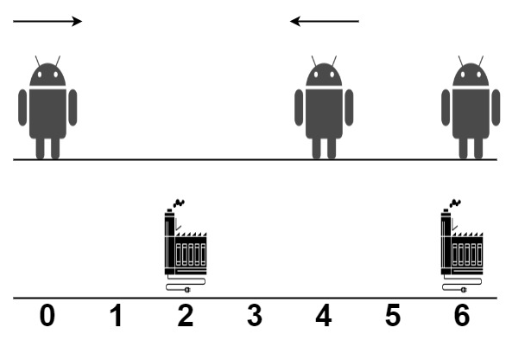

0번 로봇과 1번 로봇은 첫번째 공장까지 가기 위해 2씩 이동한다

• 2 * 2 = 4

2번 로봇은 두번째 공장에 가기 위해 이동할 필요가 없다.

• 0 * 1 = 0
• 정답은 4 + 0 = 4

제한

• $1 <= robot.length, factory.length <= 100$
• $factory[j].length == 2$
• $-10^9 <= robot[i], positionj <= 10^9$
• $0 <= limit_j <= robot.length$

풀이

• 일단 먼저 모든 공장을 제한의 수만큼 곱해 제한이 1개인 여러개의 공장이 있는것 처럼 한다.
• 로봇과 공장 위치를 전부 오름차순으로 정렬한다.
• 그 후 DP는 특정 index의 로봇이 특정 index의 공장에서 고칠지 말지로 결정한다.

재귀적 풀이

class Solution:
    def minimumTotalDistance(self, robot: List[int], factory: List[List[int]]) -> int:
        robot.sort()
        factory.sort()

        factory_position = []

        for location, limit in factory:
            for _ in range(limit):
                factory_position.append(location)

        cache = [[-1] * 10001 for _ in range(101)]

        def check(
            robot_index, factory_index
        ) -> int:
            if robot_index == len(robot):
                return 0
            if factory_index == len(factory_position):
                return 10**12

            if cache[robot_index][factory_index] != -1:
                return cache[robot_index][factory_index]

            ans = min(check(robot_index + 1, factory_index + 1) + abs(robot[robot_index] - factory_position[factory_index]), check(robot_index, factory_index + 1))

            cache[robot_index][factory_index] = ans

            return ans

        return check(0, 0)

• 로봇이 전부 고쳐지지 않았는데 끝에 도달한 경우는 절대 도달 불가능한 값을 넣었다.

Iterative 한 접근과 이해

• 원래는 recursive 한 접근에서 iterative 한 접근으로 바꾸는걸 거의 못했는데 이번 문제는 떠올리기가 쉬웠다.
• Base case들을 먼저 설정하고 호출 대신 index로 접근하는 방식을 선택했다.

class Solution:
    def minimumTotalDistance(self, robot: List[int], factory: List[List[int]]) -> int:
        robot.sort()
        factory.sort()

        factory_position = []

        for location, limit in factory:
            for _ in range(limit):
                factory_position.append(location)

        dp = [[0 for _ in range(len(factory_position) + 1)] for _ in range(len(robot) + 1)]

        for i in range(len(robot)):
            dp[i][len(factory_position)] = 10 ** 12

        for robot_index in range(len(robot) - 1, -1, -1):
            for factory_index in range(len(factory_position) - 1, -1, -1):
                dp[robot_index][factory_index] = min(dp[robot_index + 1][factory_index + 1] + abs(robot[robot_index] - factory_position[factory_index]), dp[robot_index][factory_index + 1])


        return min(dp[0])