Leetcode 2467. Most Profitable Path in a Tree

문제

There is an undirected tree with n nodes labeled from 0 to n - 1, rooted at node 0. You are given a 2D integer array edges of length n - 1 where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.

At every node i, there is a gate. You are also given an array of even integers amount, where amount[i] represents:

the price needed to open the gate at node i, if amount[i] is negative, or,
the cash reward obtained on opening the gate at node i, otherwise.
The game goes on as follows:

Initially, Alice is at node 0 and Bob is at node bob.
At every second, Alice and Bob each move to an adjacent node. Alice moves towards some leaf node, while Bob moves towards node 0.
For every node along their path, Alice and Bob either spend money to open the gate at that node, or accept the reward. Note that:
If the gate is already open, no price will be required, nor will there be any cash reward.
If Alice and Bob reach the node simultaneously, they share the price/reward for opening the gate there. In other words, if the price to open the gate is c, then both Alice and Bob pay c / 2 each. Similarly, if the reward at the gate is c, both of them receive c / 2 each.
If Alice reaches a leaf node, she stops moving. Similarly, if Bob reaches node 0, he stops moving. Note that these events are independent of each other.
Return the maximum net income Alice can have if she travels towards the optimal leaf node.

0부터 n-1까지 레이블이 지정된 n개의 노드로 이루어진 무방향 트리가 있으며, 루트는 노드 0입니다. n-1 길이의 2D 정수 배열 edges가 주어지며, 여기서 edges[i] = [ai, bi]는 트리에서 노드 ai와 노드 bi 사이에 간선이 있음을 나타냅니다.

각 노드 i에는 게이트가 있습니다. 또한 짝수 정수 배열 amount가 주어지며, amount[i]는 다음을 나타냅니다:

• amount[i]가 음수이면 노드 i의 게이트를 여는 데 필요한 비용,
• 그렇지 않으면 노드 i에서 게이트를 열 때 얻는 현금 보상.

게임은 다음과 같이 진행됩니다:

• 처음에 앨리스는 노드 0에 있고, 밥은 노드 bob에 있습니다.
• 매 초마다 앨리스와 밥은 각각 인접한 노드로 이동합니다. 앨리스는 리프 노드(잎 노드)를 향해 이동하고, 밥은 노드 0을 향해 이동합니다.
• 경로상의 각 노드에서 앨리스와 밥은 게이트를 열기 위해 돈을 지출하거나 보상을 받습니다. 다음을 유의하세요:
  • 게이트가 이미 열려 있다면 비용이 필요 없으며, 현금 보상도 없습니다.
  • 앨리스와 밥이 동시에 노드에 도달하면, 그 노드에서 게이트를 열 때의 비용/보상을 나눠 가집니다. 즉, 게이트를 여는 비용이 c라면 둘 다 c / 2씩 지불하고, 보상이 c라면 둘 다 c / 2씩 받습니다.
  • 앨리스가 리프 노드에 도달하면 이동을 멈춥니다. 마찬가지로 밥이 노드 0에 도달하면 이동을 멈춥니다. 이 두 이벤트는 서로 독립적입니다.

앨리스가 최적의 리프 노드를 향해 이동할 때 얻을 수 있는 최대 순수익을 반환하세요.

---

예시

입력: edges = [[0,1],[1,2],[1,3],[3,4]], bob = 3, amount = [-2,4,2,-4,6]
출력: 6

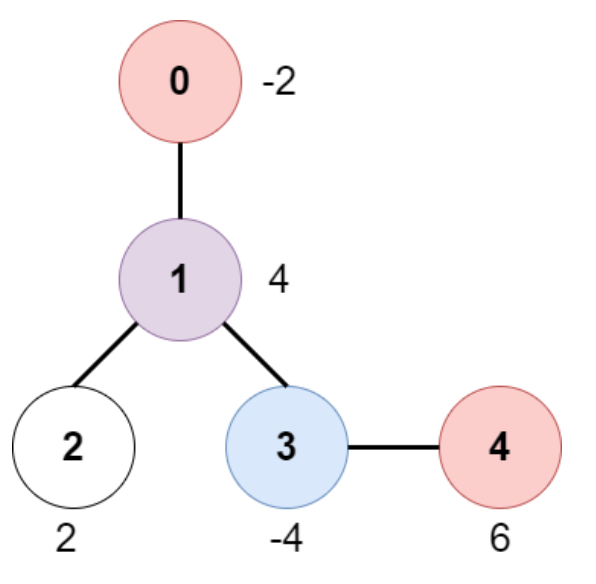
설명:
위의 다이어그램은 주어진 트리를 나타냅니다. 게임은 다음과 같이 진행됩니다:

• 앨리스는 처음에 노드 0에 있고, 밥은 노드 3에 있습니다. 각각의 노드에서 게이트를 엽니다.
  앨리스의 순수익은 이제 -2가 됩니다.
• 앨리스와 밥 모두 노드 1로 이동합니다.
  두 사람이 동시에 이곳에 도달했으므로, 함께 게이트를 열고 보상을 나눠 가집니다.
  앨리스의 순수익은 -2 + (4 / 2) = 0이 됩니다.
• 앨리스는 노드 3으로 이동합니다. 밥이 이미 이곳의 게이트를 열었으므로 앨리스의 수익은 변하지 않습니다.
  밥은 노드 0으로 이동하고, 더 이상 이동하지 않습니다.
• 앨리스는 노드 4로 이동하여 그곳의 게이트를 엽니다. 그녀의 순수익은 0 + 6 = 6이 됩니다.
  이제 앨리스와 밥 모두 더 이상 이동할 수 없으므로 게임이 종료됩니다.
  앨리스가 더 높은 순수익을 얻는 것은 불가능합니다.

---

제한

• $2 <= n <= 10^5$
• $edges.length == n - 1$
• $edges[i].length == 2$
• $0 <= a_i, b_i < n$
• $a_i != b_i$
• 반드시 올바른 tree가 생성된다.
• $1 <= bob < n$
• $amount.length == n$
• amount 는 [-104, 104] 범위의 값을 가지는 짝수의 배열이다.

---

풀이

1. bob의 위치를 찾고 root까지 경로를 찾는다.
2. bob이 언제 경로를 찾아갔는지 적고, 이를 이용해 alice에서 leaf node까지 bfs로 최대 값을 찾는다.

class Solution:
    def mostProfitablePath(self, edges: List[List[int]], bob: int, amount: List[int]) -> int:
        graph = defaultdict(list)
        degree = [0] * len(amount)

        for e1, e2 in edges:
            graph[e1].append(e2)
            graph[e2].append(e1)

            degree[e1] += 1
            degree[e2] += 1

        leaves = set()

        for i in range(len(amount)):
            if degree[i] == 1 and i != 0:
                leaves.add(i)

        path = []

        chk = [False] * len(amount)

        def pathfinder(current: int, path_list: list) -> bool:
            nonlocal path
            path_list.append(current)
            chk[current] = True
            if current == 0:
                path = path_list[:]
                return True
            for to in graph[current]:
                if not chk[to]:
                    if pathfinder(to, path_list):
                        return True
            path_list.pop()
            return False

        pathfinder(bob, [])

        bobtime = [-1] * len(amount)

        i = 0

        for p in path:
            bobtime[p] = i
            i += 1

        bfs = deque()
        chk = [False] * len(amount)
        bfs.append((0, 0, amount[0]))

        ans = -float('inf')

        while bfs:
            position, time, value = bfs.popleft()
            chk[position] = True

            if position in leaves:
                ans = max(ans, value)
                continue

            for to in graph[position]:
                if chk[to]:
                    continue

                if bobtime[to] == -1 or bobtime[to] > time + 1:
                    bfs.append((to, time + 1, value + amount[to]))
                elif bobtime[to] == time + 1:
                    bfs.append((to, time + 1, value + (amount[to] // 2)))
                else:
                    bfs.append((to, time + 1, value))

        return ans