Leetcode 2812. Find the Safest Path in a Grid

문제

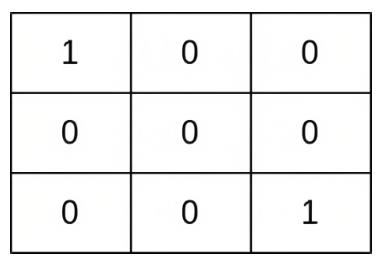
You are given a 0-indexed 2D matrix grid of size n x n, where (r, c) represents:

A cell containing a thief if grid[r][c] = 1
An empty cell if grid[r][c] = 0
You are initially positioned at cell (0, 0). In one move, you can move to any adjacent cell in the grid, including cells containing thieves.

The safeness factor of a path on the grid is defined as the minimum manhattan distance from any cell in the path to any thief in the grid.

Return the maximum safeness factor of all paths leading to cell (n - 1, n - 1).

An adjacent cell of cell (r, c), is one of the cells (r, c + 1), (r, c - 1), (r + 1, c) and (r - 1, c) if it exists.

The Manhattan distance between two cells (a, b) and (x, y) is equal to |a - x| + |b - y|, where |val| denotes the absolute value of val.

N*N 의 그리드가 있다.
그리드 내의 1은 그 칸에 도둑이 있음을 의미하며
한 위치로 부터 가장 가까운 도둑과의 맨해튼 거리를 안전거리라고 부른다.

맨해튼 거리

• x축의 거리와 y축의 거리를 합산한것
• Ex. 0, 0 과 3, 4 의 맨해튼 거리는 3 - 0 더하기 4 - 0 인 7이다.

0, 0 좌표로부터 N-1, N-1 좌표로 가는 경로가 여러개 존재할 텐데, 경로에 포함하는 노드들의 안전거리중 최소값이 가장 큰 경로가 있을때

• 즉, 가장 안전한 경로

그 경로의 최소 안전거리를 구하시오

• 가장 안전한 거리의 가장 위험한 부분의 안전 거리.

---

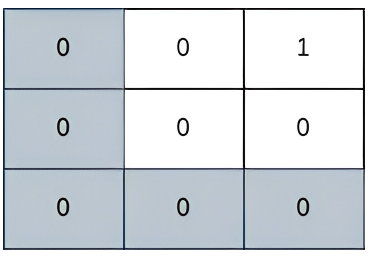
예시

• 위 이미지에서 안전거리는 전부 2이다.
• 2

---

제한

• $1 <= grid.length == n <= 400$
• $grid[i].length == n$
• 그리드의 값은 반드시 0 ( 도둑없음 ) 과 1 ( 도둑 있음 ) 만 존재한다.
• 그리드엔 반드시 하나 이상의 도둑이 존재한다.

---

풀이

• 이 문제는 코드를 보고 해석해 보겠다.

class Solution:
    def maximumSafenessFactor(self, grid: List[List[int]]) -> int:
        N = len(grid)

        def in_bound(r, c):
            return min(r, c) >= 0 and max(r, c) < N
		
        # 먼저 각 0인 칸에 대해 가장 가까운 도둑의 맨해튼 거리를 측정한다.
        # 도둑의 위치로부터 bfs를 통해 구한다.
        # 근데 모든 도둑의 위치로부터 계산하며, 한번 거리가 계산 된 칸은 제외한다!
        def precompute():
            q = collections.deque()
            min_dist = {}
            # 도둑의 위치
            for r in range(N):
                for c in range(N):
                    if grid[r][c]:
                        q.append([r, c, 0])
                        min_dist[(r, c)] = 0

            while q:
                r, c, dist = q.popleft()
                nei = [[r+1, c], [r-1, c], [r, c+1], [r, c-1]]
                for r2, c2 in nei:
                    if in_bound(r2, c2) and (r2, c2) not in min_dist:
                        min_dist[(r2, c2)] = dist + 1
                        q.append([r2, c2, dist + 1])

            return min_dist

        min_dist = precompute()
        maxHeap = [(-min_dist[(0, 0)], 0, 0)]
        visit = set()
        visit.add((0, 0))

		# 구한 거리의 maxHeap을 사용한다.
        while maxHeap:
            dist, r, c = heapq.heappop(maxHeap)
            dist = -dist
            if (r, c) == (N-1, N-1):
                return dist
            nei = [[r+1, c], [r-1, c], [r, c+1], [r, c-1]]
            # 한칸 거리의 모든 경로에서
            for r2, c2 in nei:
            # 그리드 내부에 속하면서 한번도 가지 않았던 곳에 
                if in_bound(r2, c2) and (r2, c2) not in visit:
                    visit.add((r2, c2))
                    # 가게 된다면 안전거리 최소값은 기존의 안전거리 최소값과 현재 안전거리의 최솟값이 될것이다.
                    dist2 = min(dist, min_dist[(r2, c2)])
                    heapq.heappush(maxHeap, (-dist2, r2, c2))