Leetcode 3068. Find the Maximum Sum of Node Values

문제

There exists an undirected tree with n nodes numbered 0 to n - 1. You are given a 0-indexed 2D integer array edges of length n - 1, where edges[i] = [ui, vi] indicates that there is an edge between nodes ui and vi in the tree. You are also given a positive integer k, and a 0-indexed array of non-negative integers nums of length n, where nums[i] represents the value of the node numbered i.

Alice wants the sum of values of tree nodes to be maximum, for which Alice can perform the following operation any number of times (including zero) on the tree:

Choose any edge [u, v] connecting the nodes u and v, and update their values as follows:
nums[u] = nums[u] XOR k
nums[v] = nums[v] XOR k
Return the maximum possible sum of the values Alice can achieve by performing the operation any number of times.

n개 노드(0 ~ n-1)를 가진 무방향 그래프와 노드들의 가중치 및 두 노드로 구성된 간선들의 배열이 주어진다.
그래프는 반드시 사이클을 포함하지 않는다.
그리고 정수 k가 주어지는데, 사용자는 k를 이용해 특정 연산을 수행할수 있다.
한 간선을 잡아 두 점의 가중치에 전부 k로 XOR연산을 할수 있다!
위 연산은 무제한번 수행할수 있을때, 가중치의 최대 합을 구하시오.

예시

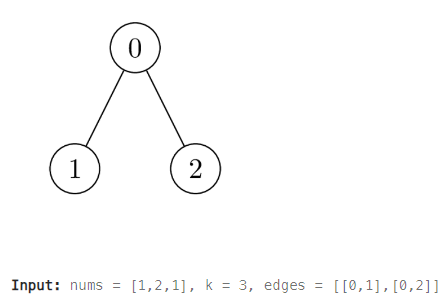
• 참고
  • 0번 노드: 가중치 1
  • 1번 노드: 가중치 2
  • 2번 노드: 가중치 1
  • K값: 3
• 0-1 을 잇는 간선에 연산을 수행한다.
  • 0번 노드의 가중치가 1 ^ 3 = 2 가 되고
  • 1번 노드의 가중치가 2 ^ 3 = 1 이 된다.
• 1-2 를 잇는 간선에 연산을 수행한다.
  • 1번 노드의 가중치가 1 ^ 3 = 2 가 되고
  • 2번 노드의 가중치가 1 ^ 3 = 2 가 된다.
• 2 + 2 + 2 = 6으로 최대값이 된다!

제한

• $2 <= n == nums.length <= 2 * 10^4$
• $1 <= k <= 10^9$
• $0 <= nums[i] <= 10^9$
• $edges.length == n - 1$
• $edges[i].length == 2$
• $0 <= edges[i][0], edges[i][1] <= n - 1$
• 입력은 반드시 완벽하게 연결된 사이클이 없는 무방향 그래프이다.

풀이

• 이 문제를 풀기 위해선 먼저 같은 숫자로 XOR을 두번 하면 원래 숫자로 돌아온다는것을 알아야 한다.
• 또한 완전히 연결되어 있기 때문에 한 노드에서 다른 노드까지 경로가 반드시 존재한다.

위 두개를 이용해 이걸 생각해낼수 있다.

• 한 노드 A에서 B로 가는 모든 간선에 연산을 수행한다고 가정한다.
• 그렇다면 노드 A와 노드 B에는 XOR이 한번씩 수행된다.
• 하지만, 경로에 해당하는 노드들은 XOR이 두번씩 수행된다?!
• 즉, 설명은 어렵게 해 놨지만 우리는 원하는 두 노드에 XOR이 수행될수 있다는것을 알수 있다!
• 이를 이용해 XOR 연산시 가장 값이 많이 증가하는 쌍들을 찾아 XOR연산 하고 최종적으로 합을 구하면 해결 가능한 문제!

class Solution:
    def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:
    	# XOR시 늘어나는 값
        t = [(i ^ k) - i for i in nums]

		# 을 내림차순으로 정렬
        t.sort(reverse=True)값

		# 값이 증가하는 쌍을 찾아 기존의 합에 더해서 리턴한다.
        ans = sum(nums)

        index = 0

        while index + 1 < len(t):
            adder = t[index] + t[index+1]
            if adder > 0:
                ans += adder
            else:
                break
            index += 2

        return ans