Leetcode 72. Edit Distance with Python

문제

Given two strings word1 and word2, return the minimum number of operations required to convert word1 to word2.

You have the following three operations permitted on a word:

Insert a character
Delete a character
Replace a character

주어진 문자열 word1과 word2에 대해서, word1을 word2로 변환하기 위한
최소한의 명령 횟수를 리턴하시오.

문자열에는 세가지의 명령을 내릴수 있습니다.

1. 문자를 삽입하기.
2. 문자를 삭제하기.
3. 문자를 변경하기.

예시

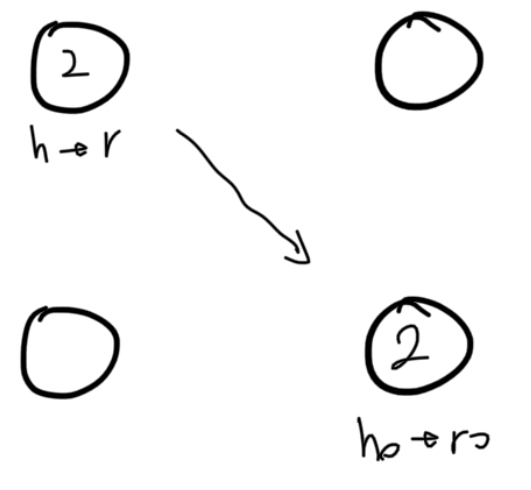
Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation: 
horse -> rorse ('h'를 'r'로 변경)
rorse -> rose ('r' 제거)
rose -> ros ('e' 제거)

제한

• 0 <= word1.length, word2.length <= 500
• 두 영단어는 소문자로만 이루어져 있다.

풀이법

접근법

• Dynamic Programming을 사용합니다.
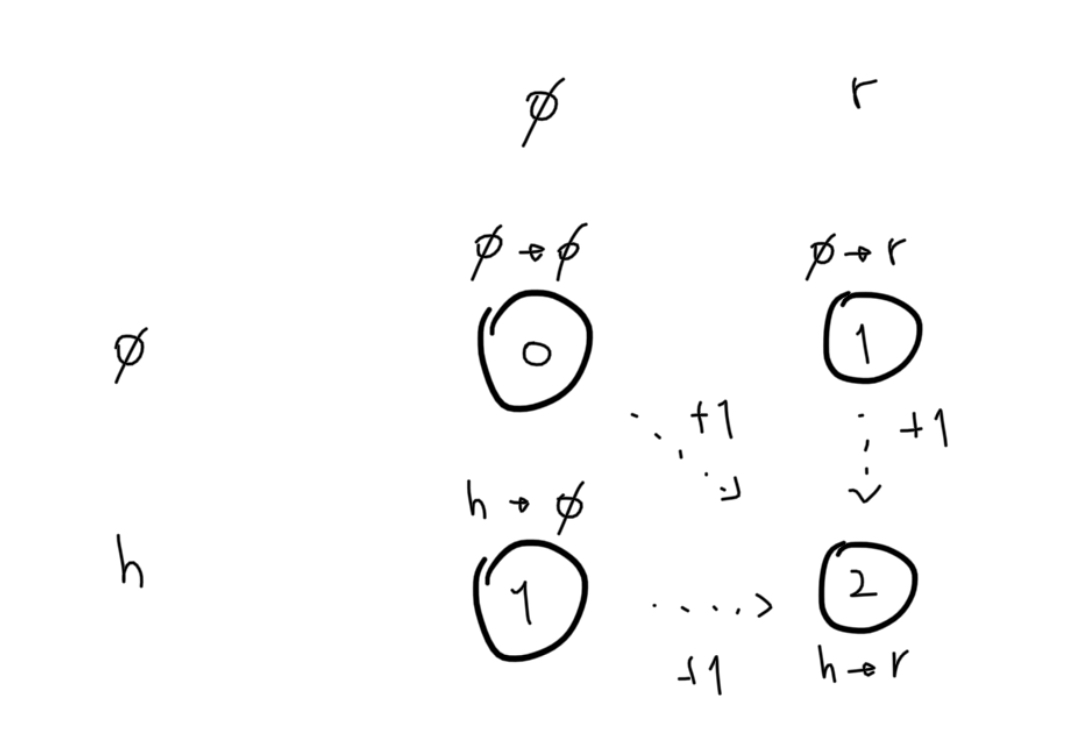
• Memoization 되는 배열의 크기는 다음과 같습니다.
  • 행 : word1의 크기 + 1
  • 열 : word2의 크기 + 1
• 각각의 i행과 j열은 다음과 같은 의미를 가집니다.
  • word1의 i번째 문자까지 를 word2에서 j번째 문자까지로 변환하기 위해 필요한 명령의 최소 갯수.
    • 이로 인해 i나 j가 0인 경우 삭제 명령만 실행되어 나머지 0이 아닌쪽의 갯수를 따라갑니다.
• 위 규칙을 통해 "horse" 가 "ros"로 변하는 예제의 배열을 그리면 아래와 같습니다, 빈 문자열은 빈 집합을 표기하는 문자를 사용했습니다.

여기서 빈 부분을 채워나가는 규칙은 2개가 있습니다.

1. word1의 맨 뒷부분과 word2의 맨 뒷부분이 같다.

• word1의 맨 뒷부분 문자와 word2의 맨 뒷부분 문자가 같다면 대각선 왼쪽 윗방향에서 그대로 가져오면 됩니다.

  앞부분을 바꾸는데 필요한 명령들만 실행하면 어차피 뒷부분은 같기때문에 추가적인 명령이 필요없기 때문입니다.

  허나 맨 뒷부분의 문자열이 같지 않다면 다음과 같은 절차를 거칩니다.

2. word1의 맨 뒷부분과 word2의 맨 뒷부분이 다르다.

이 경우 세가지 경우중 최소의 값을 고르면 됩니다.

1. 왼쪽의 명령 갯수 + 1

• 왼쪽의 경우 word2에서 필요한 문자열 하나가 없는 상태로 바뀌기 때문에 이를 추가하는 명령 하나를 더 추가하는 것입니다.

2. 왼쪽 위 명령 갯수 + 1

• 끝부분을 제외하면 나머지는 다 같도록 바뀌는데 필요한 갯수이기에 바꾸는 명령 하나만 추가합니다.

3. 윗쪽 명령 갯수 + 1

• 이미 필요한 word2의 끝부분은 만들어 졌기 때문에 word1의 끝부분을 지워줍니다.

이를 모두 완료한 뒤 memoization 배열의 오른쪽 최 하단 부분의 값을 리턴하면 됩니다.

이를 코드로 나타내면 아래와 같습니다.

class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        dp = [[0 for _ in range(len(word2)+1)] for _ in range (len(word1)+1)]

        dp[0][0] = 0
        
        for i in range(1, len(word1)+1):
            dp[i][0] = i
            
        for i in range(1, len(word2)+1):
            dp[0][i] = i
            
        for i in range(1, len(word1)+1):
            for j in range(1, len(word2)+1):
                if word1[i-1] == word2[j-1]: dp[i][j] = dp[i-1][j-1]
                else: dp[i][j] = min(dp[i-1][j-1] + 1, dp[i-1][j] + 1, dp[i][j-1] + 1)
        
        return dp[len(word1)][len(word2)]