Leetcode 84. Largest Rectangle in Histogram

문제

Given an array of integers heights representing the histogram's bar height 
where the width of each bar is 1, 
return the area of the largest rectangle in the histogram.

• 밑면의 길이가 1인 히스토그램들이 있다,
  이 히스토그램으로 만들수 있는 직사각형의 최대 크기를 구하시오.

예시

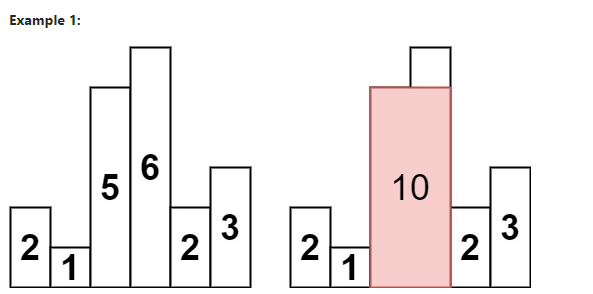
• 위 히스토그램은 10 크기의 직사각형이 최대이다.

제한

• $1 <= heights.length <= 10^5$
• $0 <= heights[i] <= 10^4$
• O(n^2) 인 알고리즘은 사용할수 없다.

풀이

• 모노토닉 스택을 사용한다.
• 값이 늘어날때는 스택에 바로 push 하는데 이때 반드시 index도 같이 push 한다.
• 값이 줄어들때는 pop하는데 이때 중요한점이 있다.
  
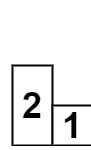
• 위는 예시에서 값이 줄어들때인데 이때 stack엔 (0, 2) 가 저장되어 있다.
  • 0번째 index에 2의 값
• 2는 1로 값이 줄어들어 더이상 2 높이의 직사각형을 만들수 없게 되었다.
• (1의 index 1 - 2의 index 0) * 2의 크기가 가장 만들수 있는 최대 크기의 직사각형이다.
  • 1 * 2 = 2
• 근데 1은 1의 크기로 직사각형을 0 index부터 만들수 있기에 스택에 저장할땐
  • (0, 1) 로 저장한다.

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        ans = 0
        stck = []

        for idx, val in enumerate(heights):
            if not stck:
                stck.append((idx, val))
            elif stck[-1][1] > val:
            	# 새로 넣을 index 계산
                s_e = 0
                while stck and stck[-1][1] > val:
                # 만들수 있는 직사각형의 최대 길이를 구해 나간다.
                    ans = max(ans, stck[-1][1] * (idx - stck[-1][0]))
                    s_e = stck[-1][0]
                    stck.pop()
                # 넣을땐 맨 마지막 기준으로
                stck.append((s_e, val))
            else:
                stck.append((idx, val))

        stck_len = len(heights)

        while stck and stck[-1][1]:
            ans = max(ans, stck[-1][1] * (stck_len - stck[-1][0]))
            stck.pop()

        return ans