
문제
Given an integer array nums and an integer k,
return the number of non-empty subarrays that have a sum divisible by k.
A subarray is a contiguous part of an array.정수 배열과 정수 k가 주어진다.
합이 k로 나누어지는 부분 배열의 갯수를 리턴하시오
부분 배열은 배열 내에서 연속한다.
예시
Input: nums = [4,5,0,-2,-3,1], k = 5
Output: 7
Explanation: 5로 나뉘는 합을 가지는 부분 배열은
[4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]
총 7개 있다.제한
- 1 <= nums.length <= 3 * 10^4
- -10^4 <= nums[i] <= 10^4
- 2 <= k <= 10^4
풀이법
배열의 부분합을 구하는 memoization 배열을 만든다.
예를 들자면 dp 배열을 하나 만들어 dp[i]는 nums 배열의 0~i번째 원소의 합을 저장하게 한다.
이렇게 했을때 dp는 부분합이 저장 되는데,
예시를 들자면 아래와 같다.
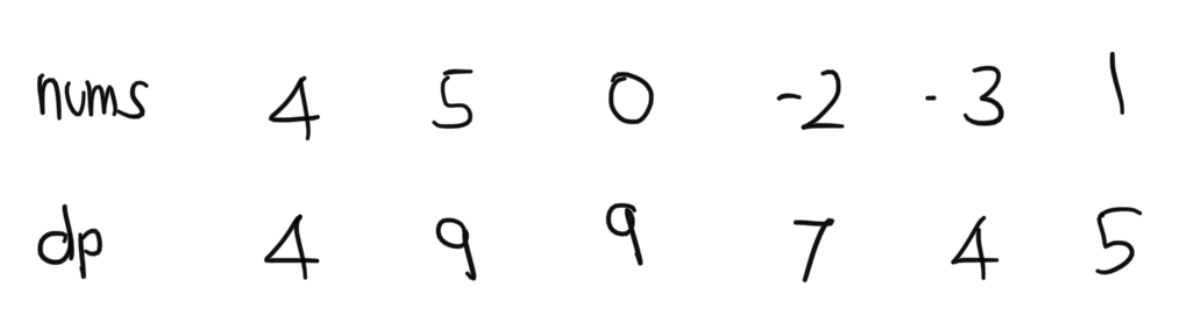
일단 여기서 먼저 알수 있는 사실은 dp를 k로 나누었을때 0이 된다는것은
nums에서 0~i번째 배열의 수를 더했을때 k로 나누어진다는 것이다.
두번째로 k로 나누어지지 않는 dp의 값들인데
이들의 k에 대한 나머지를 또 숫자로 나타내면 아래와 같다.
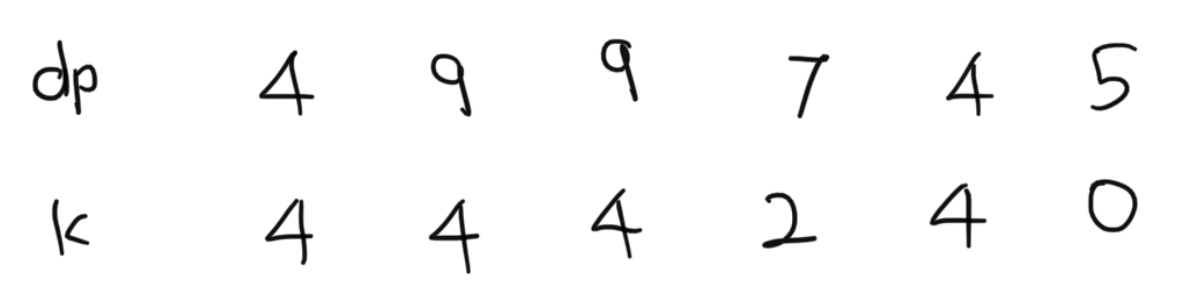
여기서 중요한건 k값이 같은 것들인데
k은 i와 j ( i < j ) 에 대해 nums에서 0 ~ i 와 0 ~ j의 부분합의 k에 대한 나머지가 같다는 것이고
0 ~ j에서 0 ~ i의 부분합을 빼면 생기는 i+1 ~ j 범위의 부분합은 k에 대한 나머지가 0이 된다는 것이다.
즉 k값에 대해서 빈도가 2 이상인, 즉 범위가 생기는 것들에 대해서 Combination을 하면 된다.
이들의 빈도를 측정해 2 이상인 것에 대해서만 nC2 계산을 하면 된다.
본인은 팩토리얼을 이용해 combination을 함수로 따로 구현했다.
import math
class Solution:
def subarraysDivByK(self, nums: List[int], k: int) -> int:
def comb(n, r):
return math.factorial(n) // (math.factorial(n-r) * math.factorial(r))
dp = [0] * (len(nums))
dp[0] = nums[0]
for i in range(1, len(nums)):
dp[i] = dp[i-1] + nums[i]
count = 0
lst = [0] * k
for i in range(len(dp)):
lst[dp[i]%k] += 1
print(lst)
for i in lst:
if i > 1:
count += comb(i, 2)
return count + lst[0]
시간복잡도 O(n)에 해결 가능해진다.
