Leetcode 1368. Minimum Cost to Make at Least One Valid Path in a Grid

문제

Given an m x n grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of grid[i][j] can be:

1 which means go to the cell to the right. (i.e go from grid[i][j] to grid[i][j + 1])
2 which means go to the cell to the left. (i.e go from grid[i][j] to grid[i][j - 1])
3 which means go to the lower cell. (i.e go from grid[i][j] to grid[i + 1][j])
4 which means go to the upper cell. (i.e go from grid[i][j] to grid[i - 1][j])
Notice that there could be some signs on the cells of the grid that point outside the grid.

You will initially start at the upper left cell (0, 0). A valid path in the grid is a path that starts from the upper left cell (0, 0) and ends at the bottom-right cell (m - 1, n - 1) following the signs on the grid. The valid path does not have to be the shortest.

You can modify the sign on a cell with cost = 1. You can modify the sign on a cell one time only.

Return the minimum cost to make the grid have at least one valid path.

• Grid에 4 방향이 새겨져 있다.
  • 1 -> 오른쪽
  • 2 -> 왼쪽
  • 3 -> 아래쪽
  • 4 -> 윗쪽
• Grid의 방향은 cost 1을 지출하고 단 한번 변경할수 있다.
• 0, 0 부터 시작해 반드시 Grid에 적힌 방향으로 이동할때 cost를 최대한 적게 지출하고 가장 오른쪽 아래까지 갈때 지출 량을 구하시오

예시

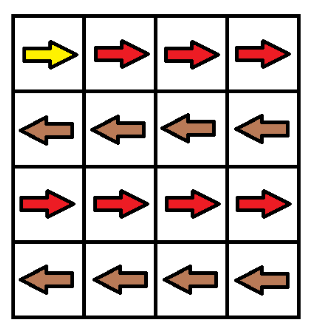
• (0, 3), (1, 3), (2, 3) 이렇게 세개를 아래로 바꾸면 된다.
• 3

제한

• $m == grid.length$
• $n == grid[i].length$
• $1 <= m, n <= 100$
• $1 <= grid[i][j] <= 4$

풀이

• BFS를 이용해 풀되, cost의 사용량중 최저가 되도록 계속 tracking 하며 구한다.
• 다만, 원래 이동하는것을 먼저 찾도록 하면 빠르게 진행된다.
  - 즉. BFS와 DFS를 섞어 사용한다.

class Solution:
    def minCost(self, grid: List[List[int]]) -> int:
        R = len(grid)
        C = len(grid[0])

        chanmap = [[float('inf')] * C for _ in range(R)]
        chanmap[0][0] = 0

        directions = [None, [0, 1], [0, -1], [1, 0], [-1, 0]]

        q = deque([(0, 0, 0)])

        while q:
            n: List[int] = q.popleft()

            if n[2] > chanmap[n[0]][n[1]]:
                continue

            row = n[0]
            col = n[1]
            changed = n[2]

            for i in range(1, 5):
                to = directions[i]
                tr = row + to[0]
                tc = col + to[1]
                if min(tr, tc) < 0 or tr >= R or tc >= C:
                    continue

                if grid[row][col] == i:
                    if chanmap[tr][tc] > changed:
                        chanmap[tr][tc] = changed
                        q.appendleft((tr, tc, changed))
                else:
                    if chanmap[tr][tc] > changed + 1:
                        chanmap[tr][tc] = changed + 1
                        q.append((tr, tc, changed + 1))

        return chanmap[R-1][C-1]