leetcode 2872. Maximum Number of K-Divisible Components

문제

There is an undirected tree with n nodes labeled from 0 to n - 1. You are given the integer n and a 2D integer array edges of length n - 1, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.

You are also given a 0-indexed integer array values of length n, where values[i] is the value associated with the ith node, and an integer k.

A valid split of the tree is obtained by removing any set of edges, possibly empty, from the tree such that the resulting components all have values that are divisible by k, where the value of a connected component is the sum of the values of its nodes.

Return the maximum number of components in any valid split.

• 노드는 0 ~ n-1까지 있으며, 무방향 트리 구조이다.
• values[i]는 i번 노드의 값(weight)이다.
• 트리에서 임의의 간선들을 제거하여 여러 개의 컴포넌트(연결 요소)를 만들 수 있다.
• 각 컴포넌트(서브트리)의 노드 값 합이 k로 나누어떨어지면(valid) 된다.
• 조건을 만족하도록 간선을 제거했을 때 만들 수 있는 컴포넌트의 최대 개수를 구하라.

예시

• 2개의 서브트리
• 답: 2

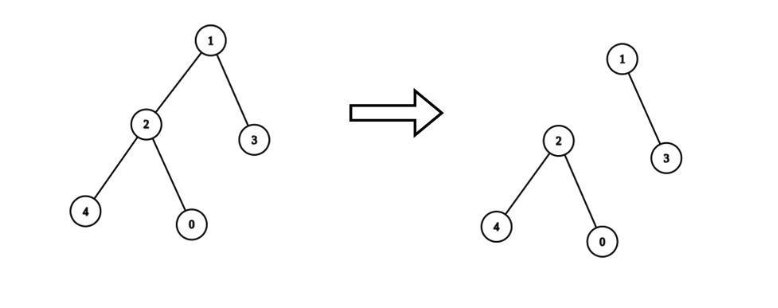
제한

• $1 <= n <= 3 * 10^4$
• $edges.length == n - 1$
• $edges[i].length == 2$
• $0 <= a_i, b_i < n$
• $values.length == n$
• $0 <= values[i] <= 10^9$
• $1 <= k <= 10^9$
• 모든 값의 합은 반드시 k에 의해 나누어진다.
• 입력값은 반드시 올바른 트리의 형태로 주어진다.

풀이

class Solution:
    def maxKDivisibleComponents(self, n: int, edges: List[List[int]], values: List[int], k: int) -> int:
        graph = defaultdict(list)

        for a, b in edges:
            graph[a].append(b)
            graph[b].append(a)

        ans = 0

        def dp(current: int, parent: int):
            nonlocal ans

            total = values[current]

            for to in graph[current]:
                if to == parent:
                    continue
                total += dp(to, current)

            if total % k == 0:
                ans += 1
            
            return total

        dp(0, -1)

        return ans

• 자신을 parent로 하는 서브트리의 합이 k로 나눠지는지 확인하고 1씩 더한다.

원리

• 일단 해당 트리는 정해진 최상위 부모 노드가 없기 때문에 0부터 시작한다.
• 트리는 기본적으로 k로 나눠진다.
• 가장 먼저 찾은 k로 나눠지는 트리를 가상으로 분리한다고 가정하면, 분리된 트리와 나머지 부분 전부 k로 나눠지는건 확정이다.
• 분리된 트리에서 또 자식 트리로 계속 이어 나가는데, 여기서도 분리된다면 분리된 부분과 나머지 부분이 k로 나눠지는게 확정이기 때문
• 즉, 계속 분리해 나가면서 최대 컴포넌트 갯수를 자연스럽게 찾게 된다.