수치해석 CH5

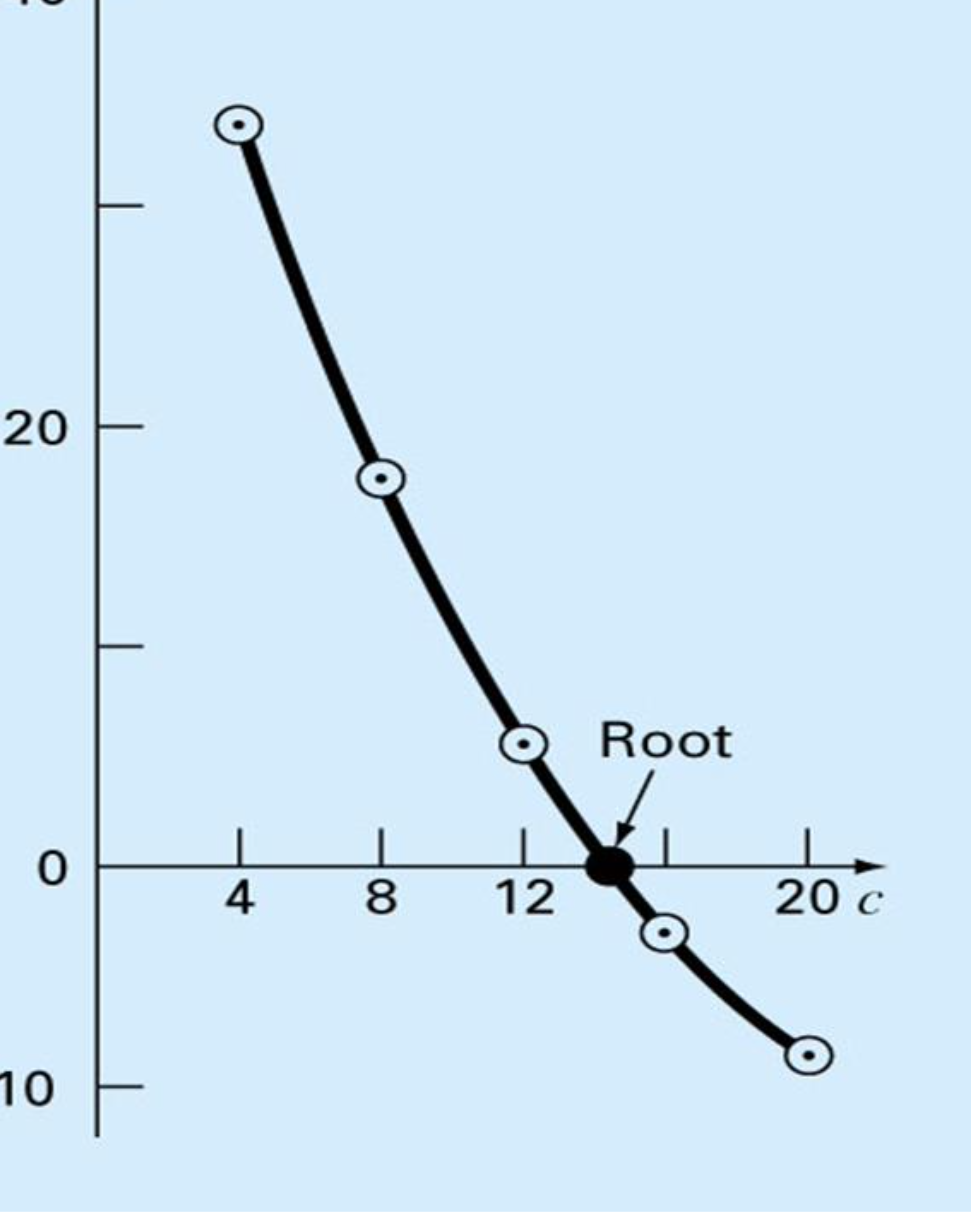
방정식의 근을 찾기

Trial & Error

• f(x) 가 0이 될 만한 x값을 추측 및 시도하는것.

Graphical Approach

• 그래프를 그려서 찾아보는것.

---

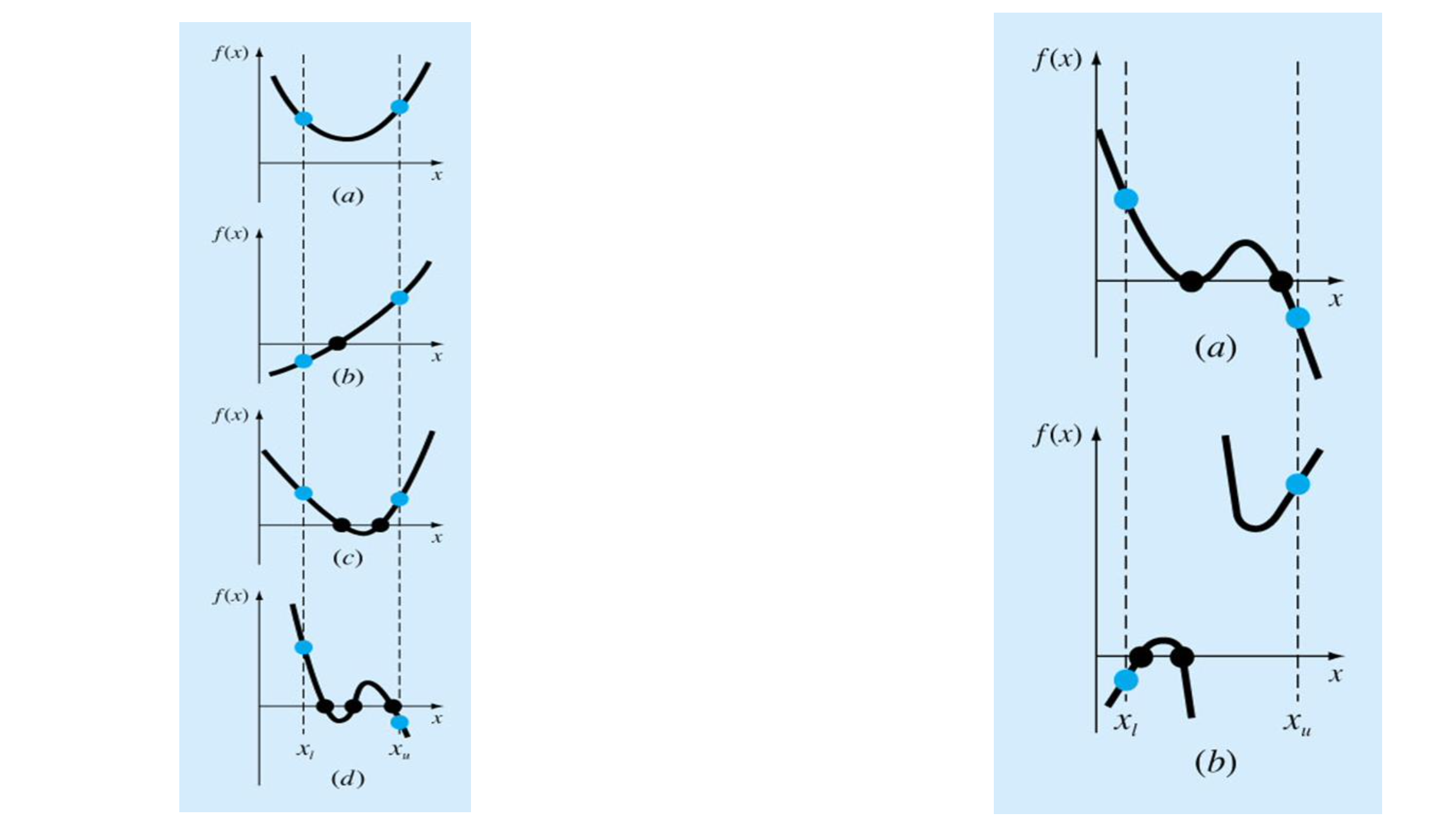
• 그래프가 이어져 있다는 전제 하에, x 위치 하나가 양수이고 하나가 음수이면 근은 반드시 존재한다.
  • 혹은 홀수개 있다.
• 둘다 양수이거나 음수일 경우 근은 없거나 짝수개 존재한다.
• 우측 1번의 경우 중근은 2개의 근으로 따져 3개의 근이 존재한다.

---

풀이법

Bisection Method

* $x_l < x_u$

1. $f(x_l) * f(x_u) < 0$ 이 성립하는 $x_l 과 x_u$ 를 찾는다.
   • 연속되는 그래프에서 이 둘 사이에는 반드시 홀수개의 근이 존재한다.
   • 찾지 못했을시 반복한다.
2. 이 둘의 평균($x_r$)을 구한다.
3. 아래 과정을 거친다.
   • $f(x_l)f(x_r) < 0$
     • 근보다 $x_r$ 이 우측에 위치, $x_u = x_r$ 로 대입.
   • $f(x_l)f(x_r) > 0$
     • 근보다 $x_r$ 이 좌측에 위치, $x_l = x_r$ 로 대입.
   • $f(x_l)f(x_r) == 0$
     • 근을 찾았다! ( $x_r$ )
   • 근을 찾지 못했으면 다시 2번으로 돌아간다.
   • 혹은 $x_r$ 기준, 상대적 오차 ( (현재추정값 - 이전추정값) / 현재추정값) 의 절댓값) 을 이용해 구할수도 있다.

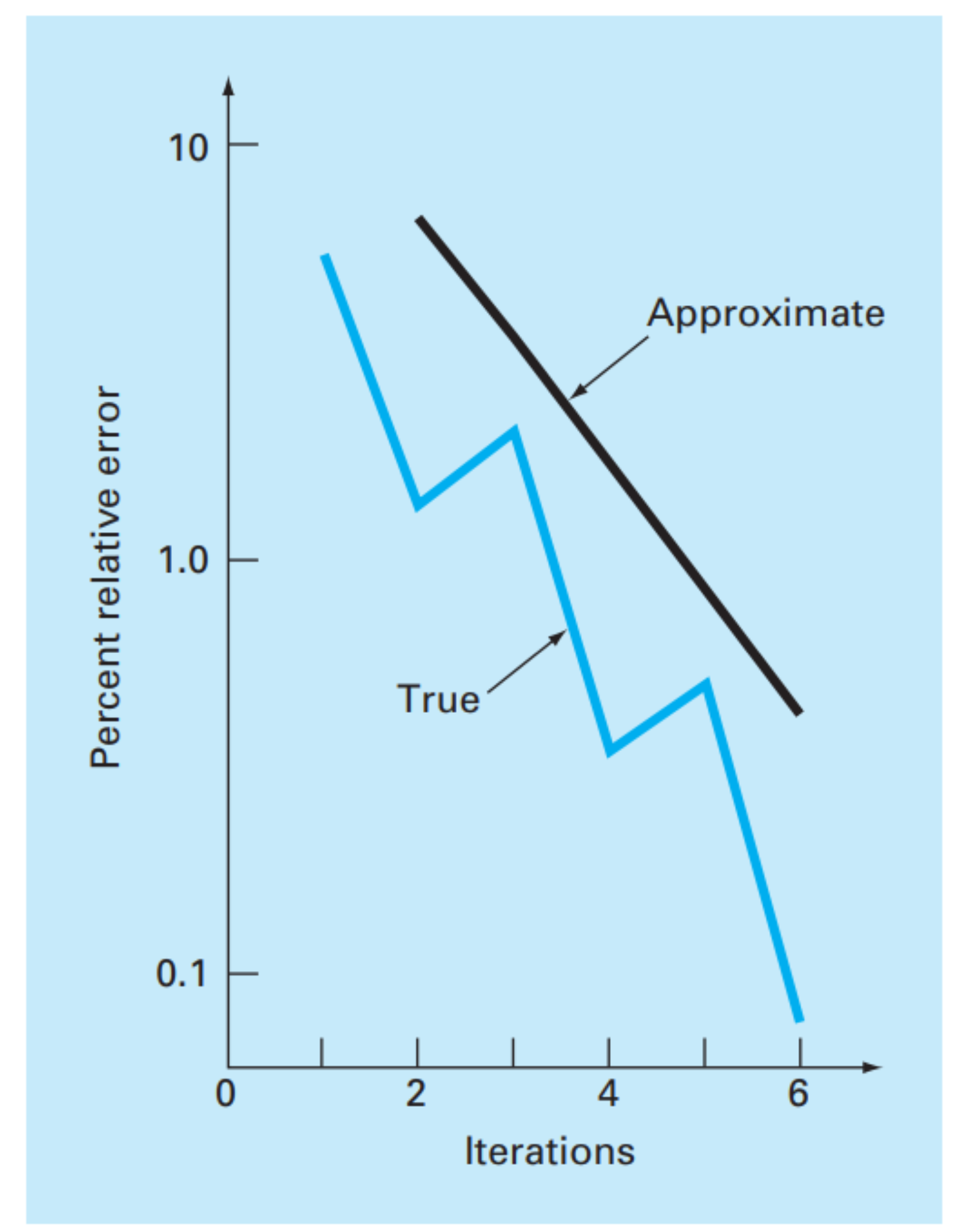
• 시도별 오차가 떨어지는 모습.
• 이진 탐색에 가까운 코드를 사용해 실제 오차는 증가와 감소를 반복한다.

---

False-Position method

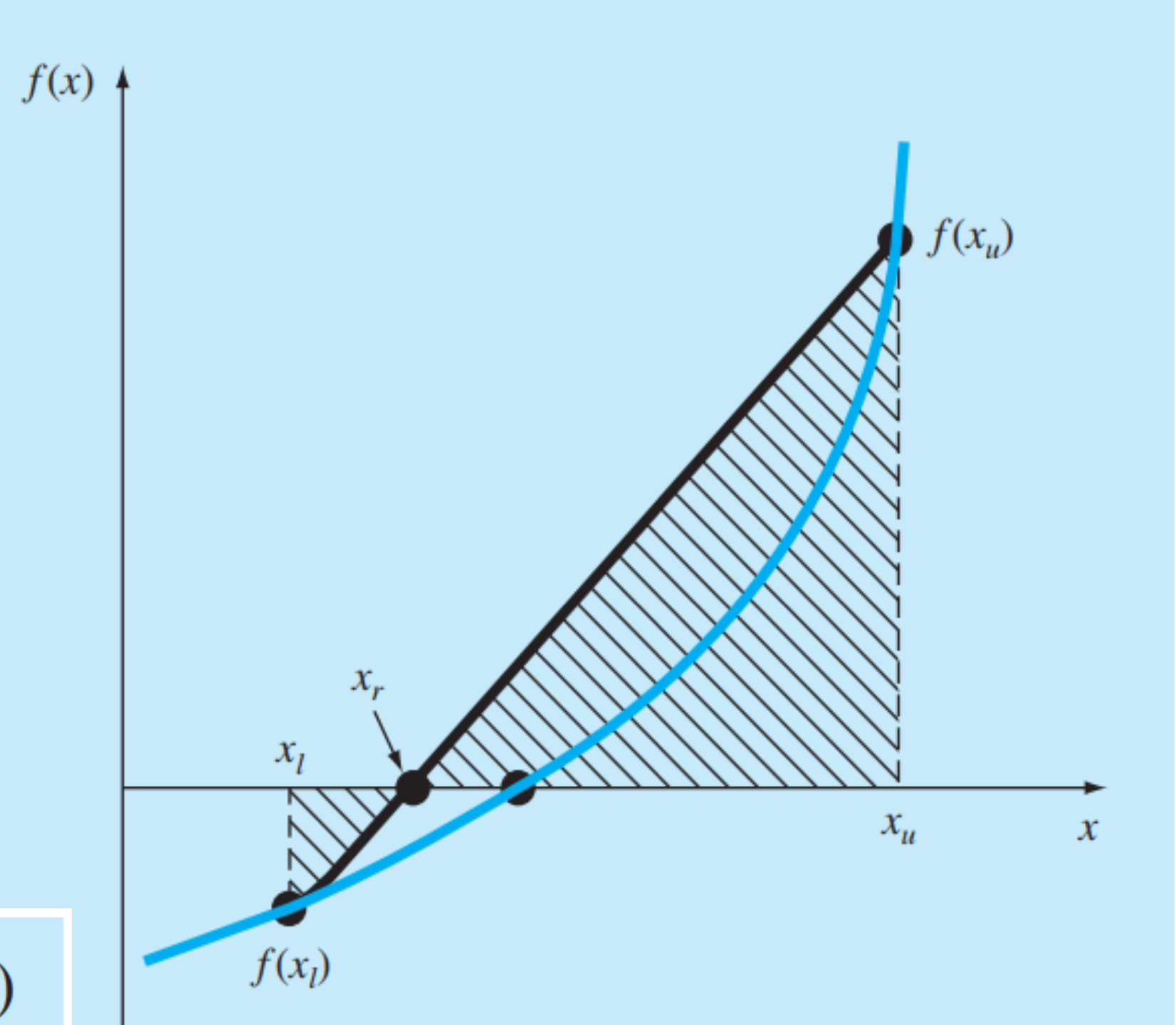
• $f(x_l) * f(x_u)$ 가 음수가 되는 두 x점을 찾는다.
• 이 두 점을 선으로 연결하면 중간에 근을 지나는 선이 완성된다.
• 이 선을 선분으로 이으면 두 삼각형을 그릴수 있다.
• 이 선이 x축에 만나는 $x_r$을 구할수 있다.
• 이 $x_r$값을 $x_l$ 에 대입한다.

• x_r을 구하는 방식

Modified false position

• 거의 대부분의 경우에 Bisection보다 성능이 좋은 방식이다.
• 좌표점 $(x_l, f(x_1))$ 과 $(x_u, f(x_u) / 2)$ 의 $x_r$을 찾는식으로 진행된다.

---

근이 여러개 존재하는 경우

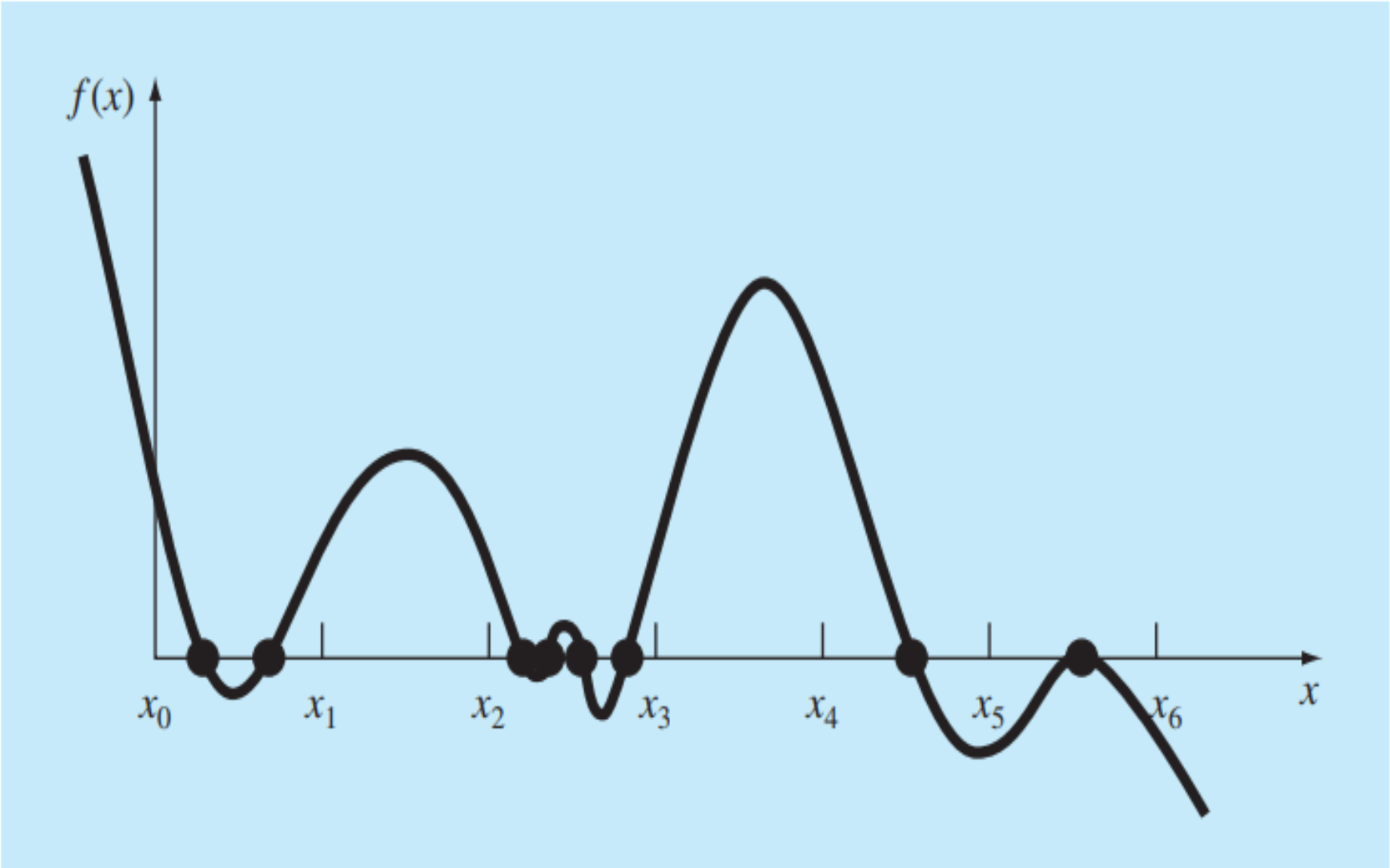
incremental search

• $x_0$ 부터 아주 작은 간격으로 한칸씩 앞으로 나가며 해당하는 y축의 값을 찾는다.
  • $x_0$ 은 첫번째 근보다 앞에 있어야 한다.
• 간격을 지났을때 해당하는 y축의 값이 부호가 반대가 되면
  Bisection혹은 False-position을 사용해 근을 계산할수 있다.
• 간격이 너무 작으면 시간이 오래 걸리고, 간격이 너무 크면 근을 지나칠수도 있다.

간격이 너무 커서 근을 지나친것을 판별하는 방법

• 찾은 두 점의 기울기를 찾으면 된다.
• 예시로 위 그래프에서 간격을 가지는 두 점이 $x_0$과 $x_1$ 일시 두 점의 기울기는 반대가 된다.
• 두 점 사이에 근이 존재 할수도 있다, 간격을 줄여 다시 확인해볼수 있을것이다.
  • 반드시 존재하지는 않는다. ( $x_3, x_4$ )