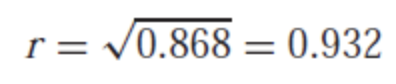수치해석 Linear Regression/

Regression - 회귀

• 기존에 관찰된 데이터를 기반으로, 특성을 잘 표현하는 수학적 모델을 만든다.
• 수식에 관계되는 여러 변수들의 값을 찾아내 새로운 값을 예측한다.
• 오류를 포함한 관찰 데이터들로부터 유효한 공식을 구할수 있다.

회귀

• 평균값으로 돌아간다는 의미를 가진다.

---

Dependent / Independent Variable

Dependent Variable

• 예측하고자 하는 변수

Independent Variable

• Dependent Variable에 영향을 주는 변수

---

Linear Regression

Simple linear regression

• u는 오차를 의미한다.

Multiple linear regression

Hyper Plain : 초평면 - 개념적으로 존재하는 여러 차원의 평면

• Y : 예측하고자 하는 Dependent Variable
• X : Y에 영향을 주는 Independent Variable
• a : y 절편

What?

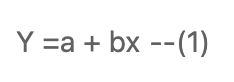
• 변수, 패러미터에 대해 선형적 (1)
  
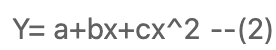
• 변수에 대해 비선형적 (2)
  
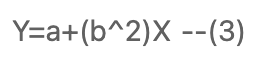
• 패러미터에 대해 비선형적 (3)
  
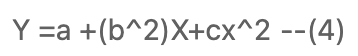
• 변수와 패러미터에 대해 비선형적 (4)
• 1, 2 가 선형 회귀에서 다루는 부분이다.
  • 패러미터가 선형적이여야 한다.
  • 패러미터를 알아내는 것이기 때문이다.

• 이식을 오차에 대해 정리하면
  
• 이와 같이 표현할수 있다.
• 여기에서 오차의 합을 최소화 하는 a0과 a1를 찾는 것이 목표이다.

Type

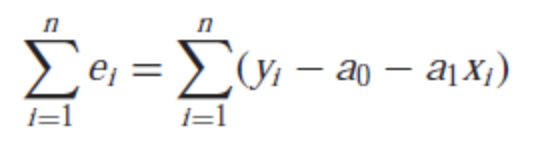
• 오차의 합
  
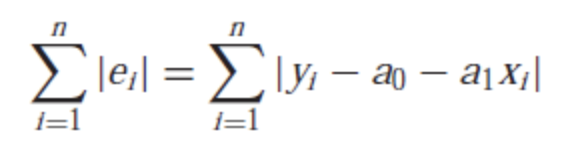
• 오차의 절댓값의 합
  
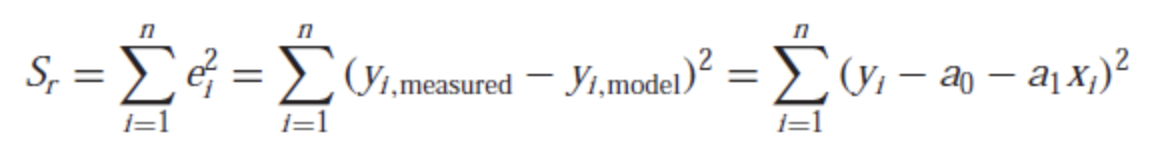
• 오차의 제곱의 합 ( $S_r$ )
• 가장 오차를 최소화 하기 좋은 이상적 형태이다.
• 오차의 제곱의 합을 최소화 하는 패러미터를 찾는다.

편미분 공식

Least-Sqaure Fit of Straight Line

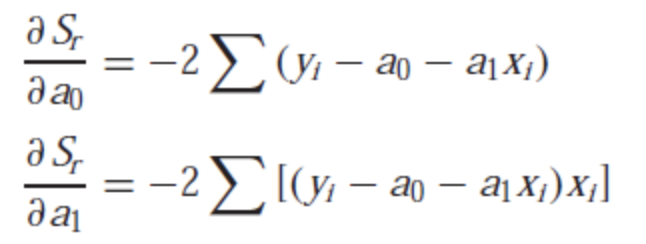
• 식을 각각의 패러미터($a_0, a_1$)에 대해 편미분한다.
• 두 식을 연립하여 $a_0, a_1$ 을 찾을수 있다.

검증

• 오차들의 표준편차를 이용한다.
  
  
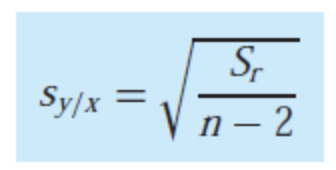
• 관측 값의 표준오차
  
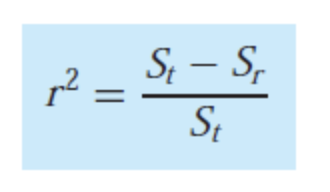
• coeffecient of determination 을 사용하기도 한다.
• 위 r^2 값을 통해 대략 몇 퍼센트 정도 선형회귀가 잘 맞는지를 확인할수 있다.
  
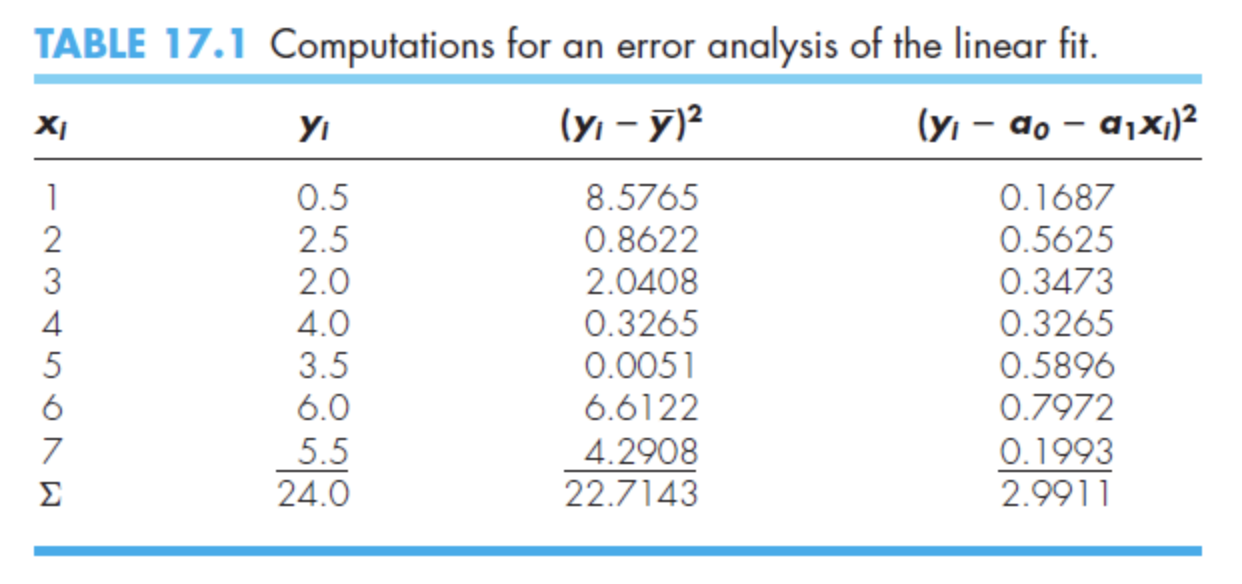
  3번 Column의 값 : y 실측값 - y평균값 의 제곱
• $S_t$ : 평균 직선으로 구한 편차 ( 평균 직선과의 오차의 합을 제곱한것 )
• $S_r$ : 찾은 직선으로 구한 편차 ( 찾은 직선과의 오차의 합을 제곱한것 )