컴파일러 CH2. Lexical Analysis

이전 이야기

• 포트란은 명시적으로 Loop 표시 가능
• LISP은 모든게 함수로 선언, Prefix notation을 사용한다
• 컴파일러 : 고급언어를 어셈블리로 변환 >> 효율적, 올바른 코드 생성, 기기 특이적 코드 생성
  • 공격적 최적화
  • 실행 오버헤드 없음
  • Dynamic compilation : LISP / Prolog - Input data에 맞춰 코드를 최적화 할 부분은 남겨두고 이외만 미리 컴파일
  • JIT compilation : 바이트코드를 실시간으로 컴파일 하고 이를 실행
  • Ahaed of time compilation : 설치가 되면서 미리 기기를 위해 반쯤 컴파일 해둠
• 인터프리터 : 코드를 한줄씩 실행 >> 인터프리터(실시간 통역) 만 작동하면 어디서든 코드가 돌아간다. JAVA Bytecode, Python
• 크로스컴파일 : 다른 플랫폼에 돌아갈수 있는 프로그램을 컴파일 >> 에뮬레이터 사용, 임베디드-모바일에 주로 사용
• 컴파일러와 인터프리터의 조합
  - 인터프리터를 위한 중간언어를 컴파일러가 생성한다. < IR >
  - python의 경우 pyc로 중간 컴파일을 실행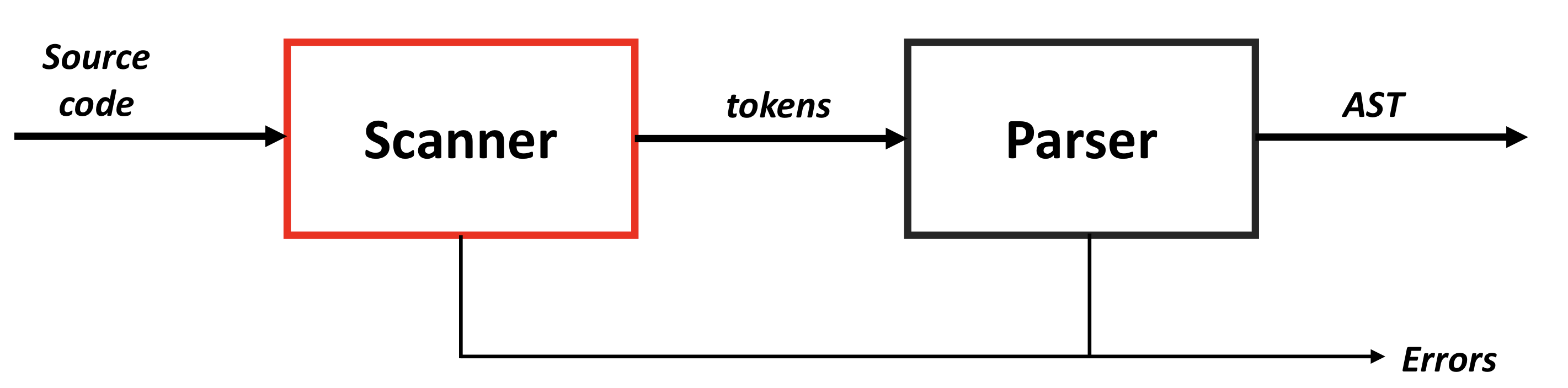
  

Scanner

• 문자열을 토큰이라고 불리는 단어들로 매핑한다.

Token

• 문법의 가장 기본적 단위
• x = y + 21; 은 아래와 같은 토큰들로 이루어진다.
  • <id, x>
  • <=>
  • <id, y>
  • <+>
  • <intliteral, 21>
  • <;>
    id = identifier

• 단어를 이루는 문자열을 lexeme(어휘소)라 부른다.

• 토큰은 <Token-Type, Value/Lexeme> 의 튜플로 구성된다.
  • Lexeme : Token으로 구별 가능한 String

• 비격식적으로 <id, x> 토큰을 "Token x" 라고도 부른다.

• 토큰으로 프로그래밍 언어에 자연어 단어를 알려준다.

Lexeme(s)

• 토큰의 패턴에 일치하는 소스코드의 문자(열) 자체
• 소스 코드

Token

• 토큰 이름과 선택적으로 존재하는 관련값의 Tuple
• 토큰 이름은 어휘 단위를 표현하는 추상적 상징입니다.

Mini C에서 사용하는 토큰 타입

• Identifier : i, j, initial
  • 식별자
• Keyword : if, for, while, int, float, bool
  • 키워드
• Operators : + - * / <= &&
  • 연산자
• Separators : { } ( ) [ ] ; ,
  • 분리자
• Literals
  • Int literals : 0, 5, 100
  • Float literals : 0.25, 1.125, 1.0
  • Bool literals : true, false
  • String literals : "hello\n"

• 정확한 토큰의 집합은 주어진 프로그래밍 언어마다 다르다!

Pattern

• 특정 토큰 타입을 설명하기 위한 룰
  
• 위 문자열의 집합은 특정 Pattern X에 의해 설명되며, 이를 Language of X라 부른다.
• Lanuage of X는 L(X)라 쓰여진다.

---

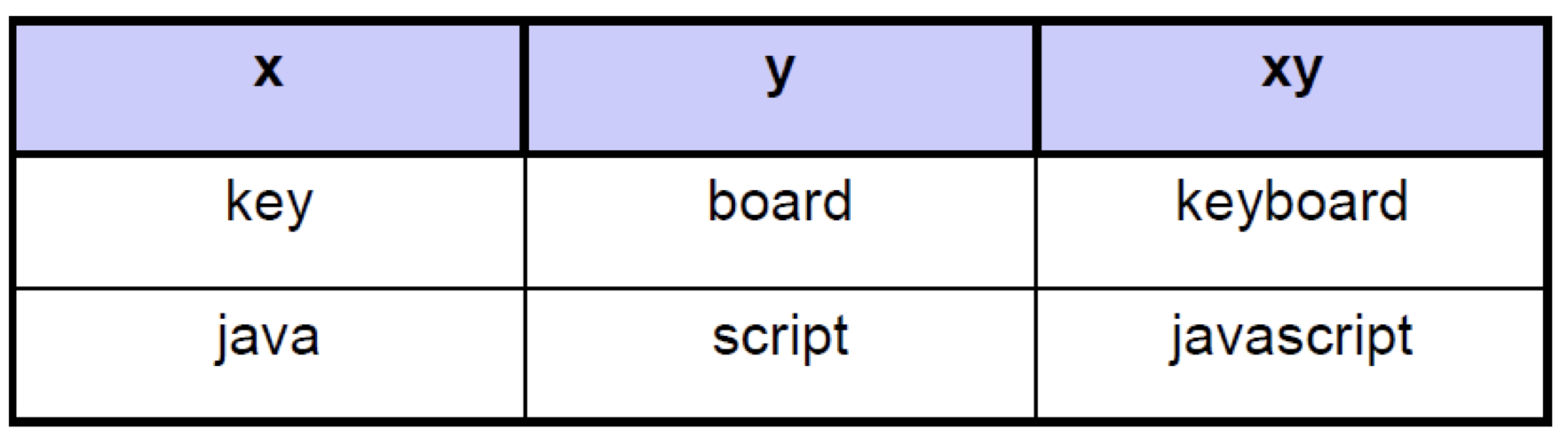
String Concatenation

• x와 y문자열이 있을때, xy는 x와 y 문자열을 합친것이다.
  

Set Operation

Union : 집합 L과 집합 M에 있는 원소 중 하나
Concatenation : 집합 L의 원소중 하나와 집합 M의 원소중 하나를 붙힘
Kleene Star : 집합 L의 원소를 계속 무작위로 선택해 0~무한 번 반복함
Positive Kleene Star : 집합 L의 원소를 계속 무작위로 선택해 1~무한 번 반복함

$L^3$ = 3번 반복

---

Regular Expression / REGEX

• Regex는 패턴을 설명하는데 사용될수 있다.
• 문자열은 유한한 집합인 알파벳 $\Sigma$ 안에있는 글자로만 이루어진다.

Alphabet $\Sigma$에 대해 Regex를 구성하는 귀납적 의미

• R1 : ε 는 {ε} 를 표기하는 Regex이다.
• R2 : a가 ∑에 있을시, a는 {a}를 표기하는 Regex이다.

x와 y가 각각 L(x)와 L(y)를 표기하는 Regex일때

• R3 Alternation : x | y 는 L(x) $\cup$ L(y)를 표기하는 Regex이다.
• R4 Concatenation : xy는 L(x)L(y)를 표기하는 Regex이다.
• R5 Closure : $x^*$는 $L(x)^*$를 표기하는 Regex이다.

$\Sigma$ = {0, 1} < 문자열을 구성하는 문자 집합 - Alphabet >

$\Sigma$ = {a, b, c}

Precedence Rule - 우선순위 규칙

• Regex의 모호함을 없애기 위해 필요하다
• Closure -> Concatenation -> Alternation
  

Regex를 이용한 토큰의 예시

1. Digit : 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
2. Letter : a | b | ... | z | A | B | ... | Z
3. 2 Char Identifier, starting with letter and followed by digit or letter
   • $Letter(Digit | Letter)$

• identifier가 숫자로만 이루어질시 정수 리터럴과 헷갈릴수 있다.
• Ambiguous 하면 안된다!

이 외 토큰 예시

• Identifier는 최소 하나의 글자를 포함하며, 첫글자는 반드시 문자열이여야 하며 이후 숫자나 문자가 올수 있다.
  • $letter(letter | digit)^*$
• Integer numbers : 첫글자는 숫자이고, 이후 0~무한개의 숫자가 반복된다.
  • $(digit)(digit)^*$
• Signed Integer Number : "+"나 "-"를 선택적으로 앞에 가지는 정수 숫자
  • $(+|-|ε)integer$

줄임 표현

1. 1회 이상의 Concatenation
   • $r^+ = rr^*$
2. 0개 혹은 1개
   • $r? = \epsilon | r$
3. 문자
   • $[a-zA-Z]$

miciC의 예시

_MiniC의 문자에는 _ (언더스코어)가 포함된다._ _자바에서는 문자와 숫자가 Unicode char set에서 가져와질수 있다_

---

Regex And Scanner

• 우리는 Regex를 lexemes에서 token으로의 매핑을 구체적으로 명시하기 위해 사용한다.

• 알고리듬의 오토마타 원리의 결과를 이용해, 우리는 자동으로 Regex에서 Recognizer를 만들어 낼수 있다.

예시 : 레지스터 이름의 확인

• 레지스터 : $r[0-9][0-9]^*$
• 레지스터에 임의의 숫자 허용
• 최소 한 자리 숫자 필요
• $\Sigma = \{r, 0, 1,..., 9\}$

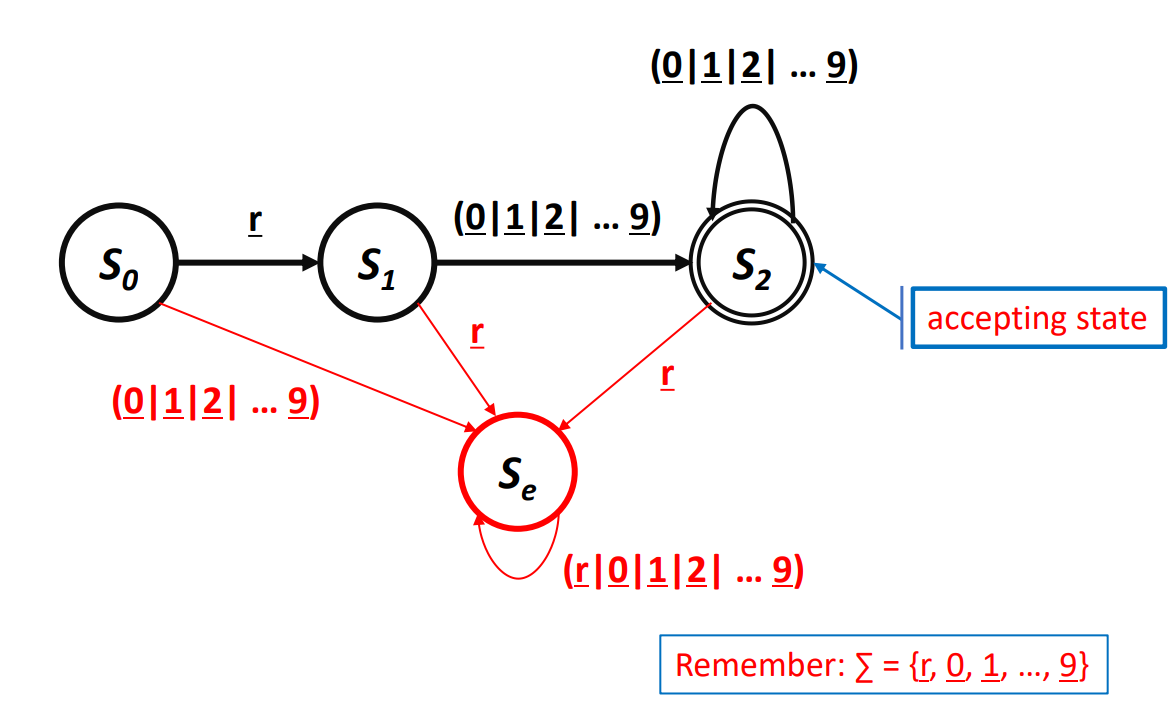
RE에 해당하는 Recognizer / DFA

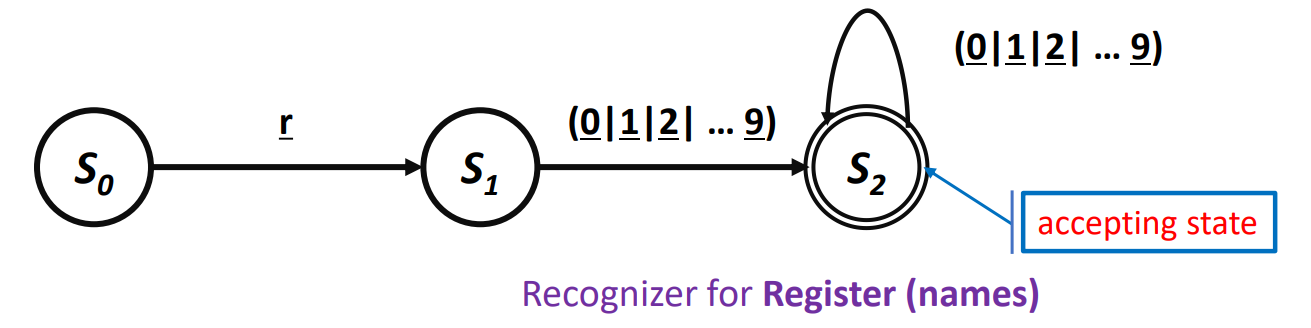
• 적히지 않은 다른 값으로 인한 Transition은 Error state인 $S_e$로 향한다.

위 DFA의 동작

• $S_0$에서 시작해 각각 문자 입력마다 Transition한다.
• DFA는 최종적으로 $S_2$에 도달하는 입력값을 Accept 한다.

• $r17 \rightarrow Accept$
• $r \rightarrow Fail$
• $1 \rightarrow S_e$

RISC-V 레지스터 예시

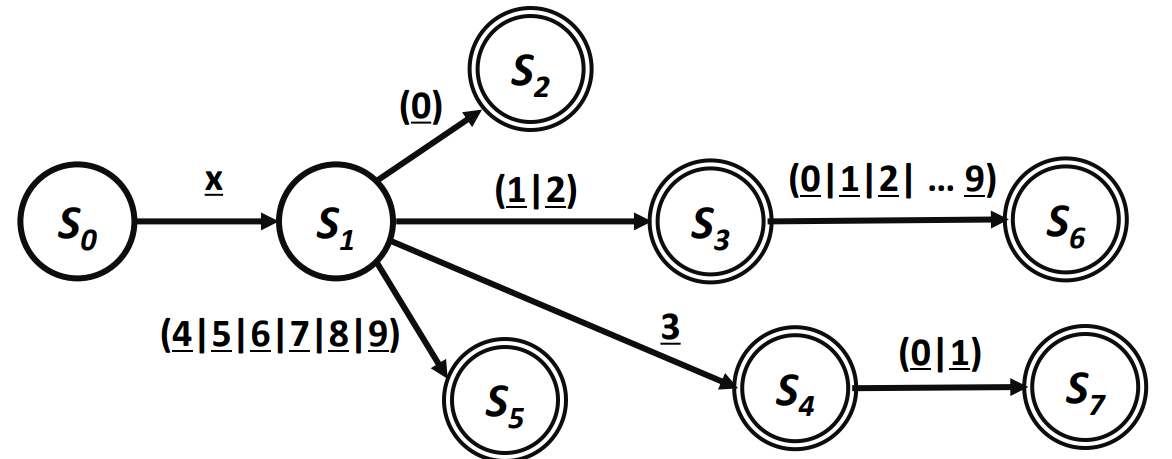
• 레지스터 번호가 0 ~ 31로 제한된다.

Error State

• $S_e$
• 올바르지 못한 입력에 대해 Transition 되는곳

---

Finite Automata / FA

• FA는 5개 튜플로 이루어진다.

$< \Sigma, S, \delta, F, I >$

• $\Sigma$ = Alphabet, 이 언어를 구성하는 Input의 목록
• $S$ = 상태의 유한집합
• $\delta$ = 전이함수
• $F$ = 최종/수용 상태들
• $I$ = 최초 상태

Transition function

$\delta$(Current State, Input) = Next State

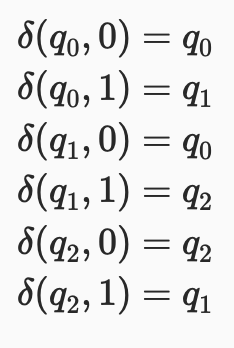
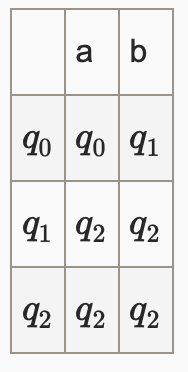
Column Index : Input
Row Index : Current State

State transition Function / Code

---

Non-deterministic Finite Automata / NFA

• 입력으로 $\epsilon$이 포함된 Regex를 구현할수 있다.
• 동일한 입력으로 하나의 State에서 여러가지 Transition을 하게 할수 있다.

예시

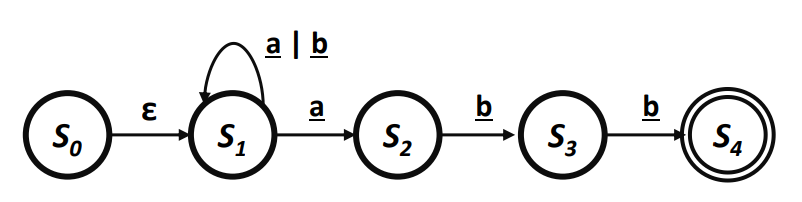
• $\epsilon$이 입력으로 주어졌을때 $S_0$가 Transition을 한다.
  • $\epsilon$ Transition은 어떤 입력도 소모하지 않는다.
• $S_1$은 a 입력에 대해 2개의 Transition을 할수 있다.

NFA / Accept State

• NFA는 String x가 $S_0$에서 Accept State로 가는 Path가 있을시 Accept한다.
• Transition $\epsilon$은 어떤 입력도 소모하지 않는다!
• NFA를 동작하기 위해, $S_0$에서 시작해 각각의 단계마다 올바른 Transition을 추측한다.

$\epsilon$ 은 NFA를 합치기 위한 일종의 접착제 역할을 한다.

NFA는 REGEX를 DFA로 만들기 위한 열쇠의 역할을 한다.

---

DFA와 NFA

• DFA는 NFA의 종류중 하나이다.
  • DFA는 $\epsilon$ Transition이 없다.
  • DFA의 전이함수는 단일값이다.
    • 특정 입력에 대해 2개의 Transition을 가질수 없다.

DFA를 NFA로 시뮬레이션

• 매우 가능함

NFA를 DFA로 시뮬레이션

• 가능한 상태의 집합으로 시뮬레이션
• 상태공간이 매우 커진다.
• 여전히 한번 입력에 1개의 문자를 사용한다.

모든 DFA와 NFA는 서로 같은 Form을 가지는 쌍이 존재한다.

---

자동화 스캐너 구축

Specification을 Code로 전환시키기

1. 입력 언어에 대한 RE를 작성한다.
2. 커다란 NFA를 만든다.
3. NFA를 Simulate 하는 DFA를 만든다.
4. DFA의 상태 갯수를 줄인다.
5. 스캐너 코드를 생성한다.

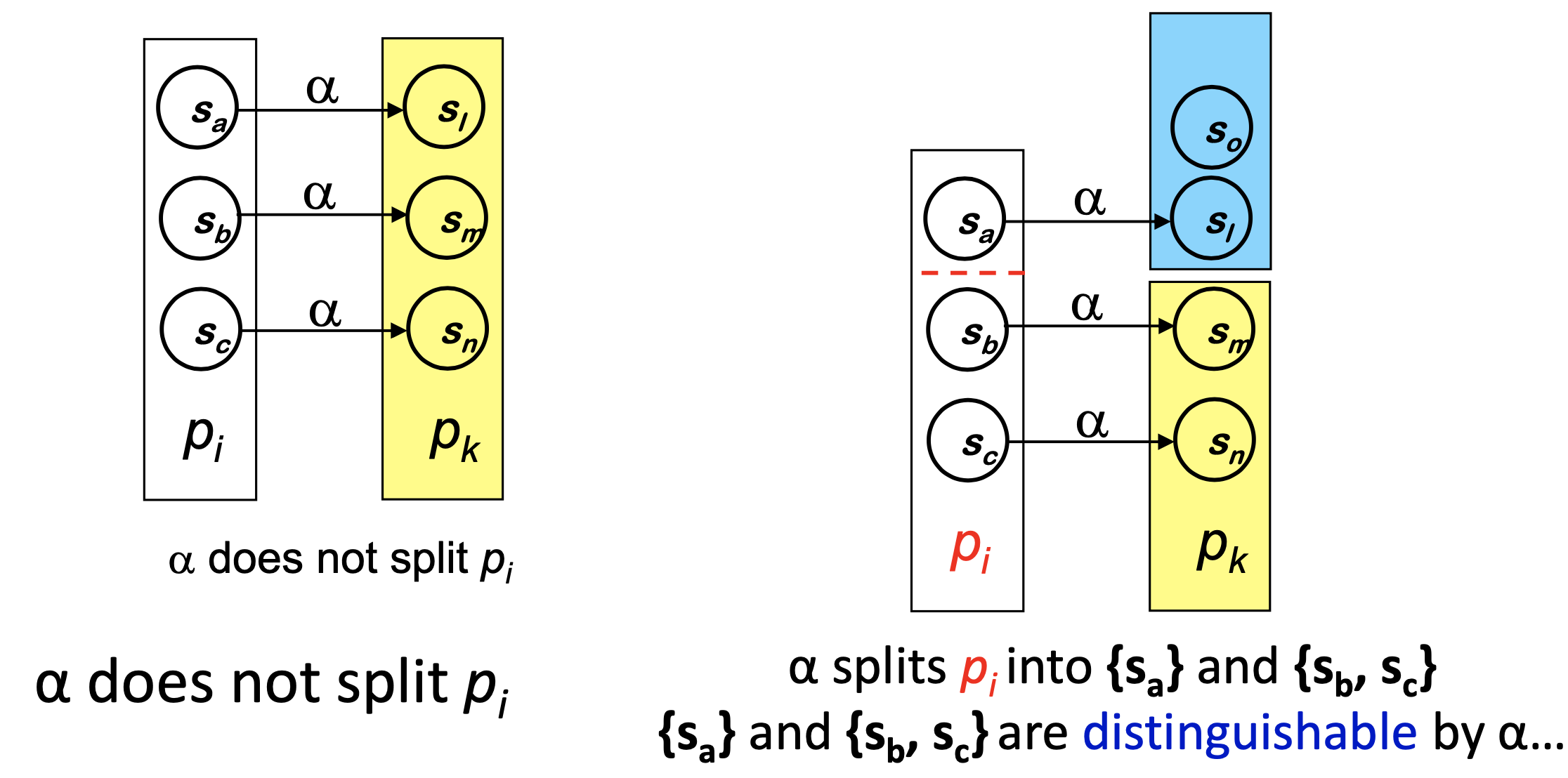
RE로 NFA 작성하기

Thompson's Construction

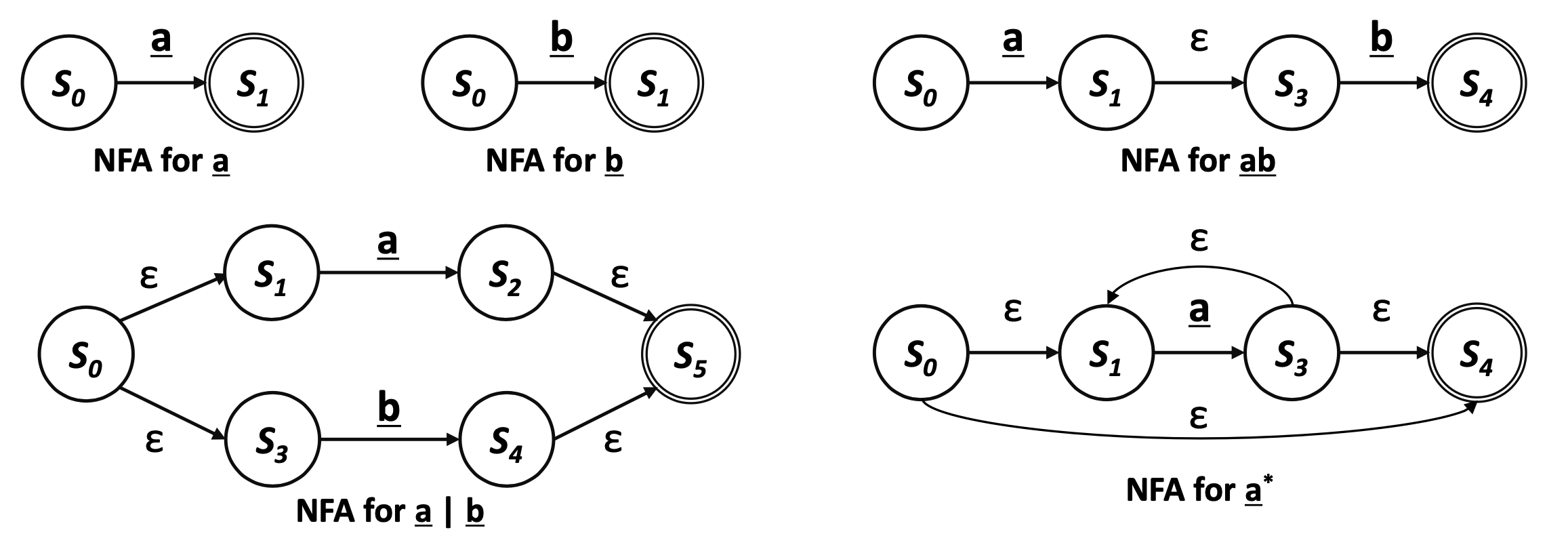
• Key Idea
  • NFA를 RE의 각 Symbol과 Operator를 통해 작성
  • 2개의 NFA를 붙힐땐 $\epsilon$ Transition 사용한다.

• 예시 : $a(b|c)^*$
  
  

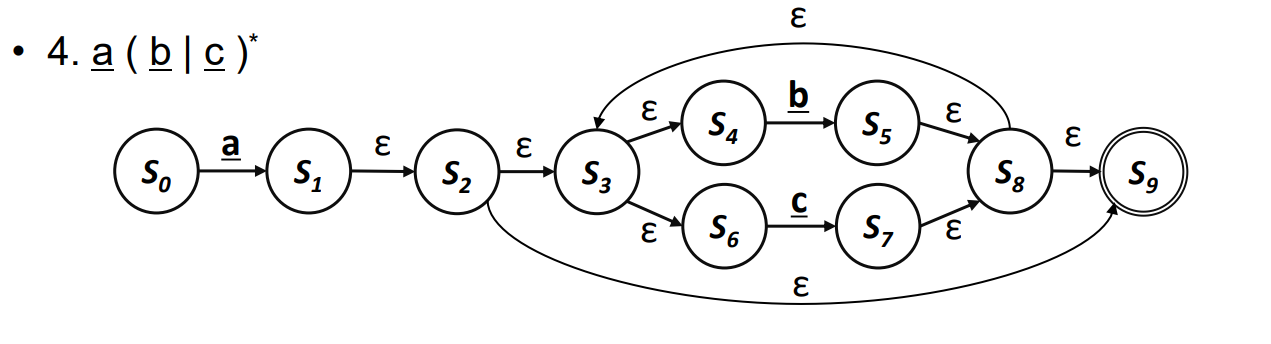
• 단순한 디자인도 가능하다
• 최종적으로 하고 싶은것.
  

Tompson's Construction - Inductive Base

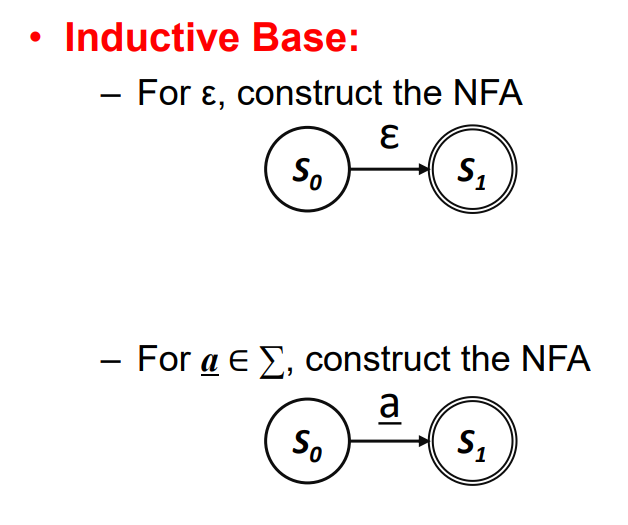
Inductive Step

• N(r)과 N(s)가 RE r과 s를 위한 NFA일때
  

---

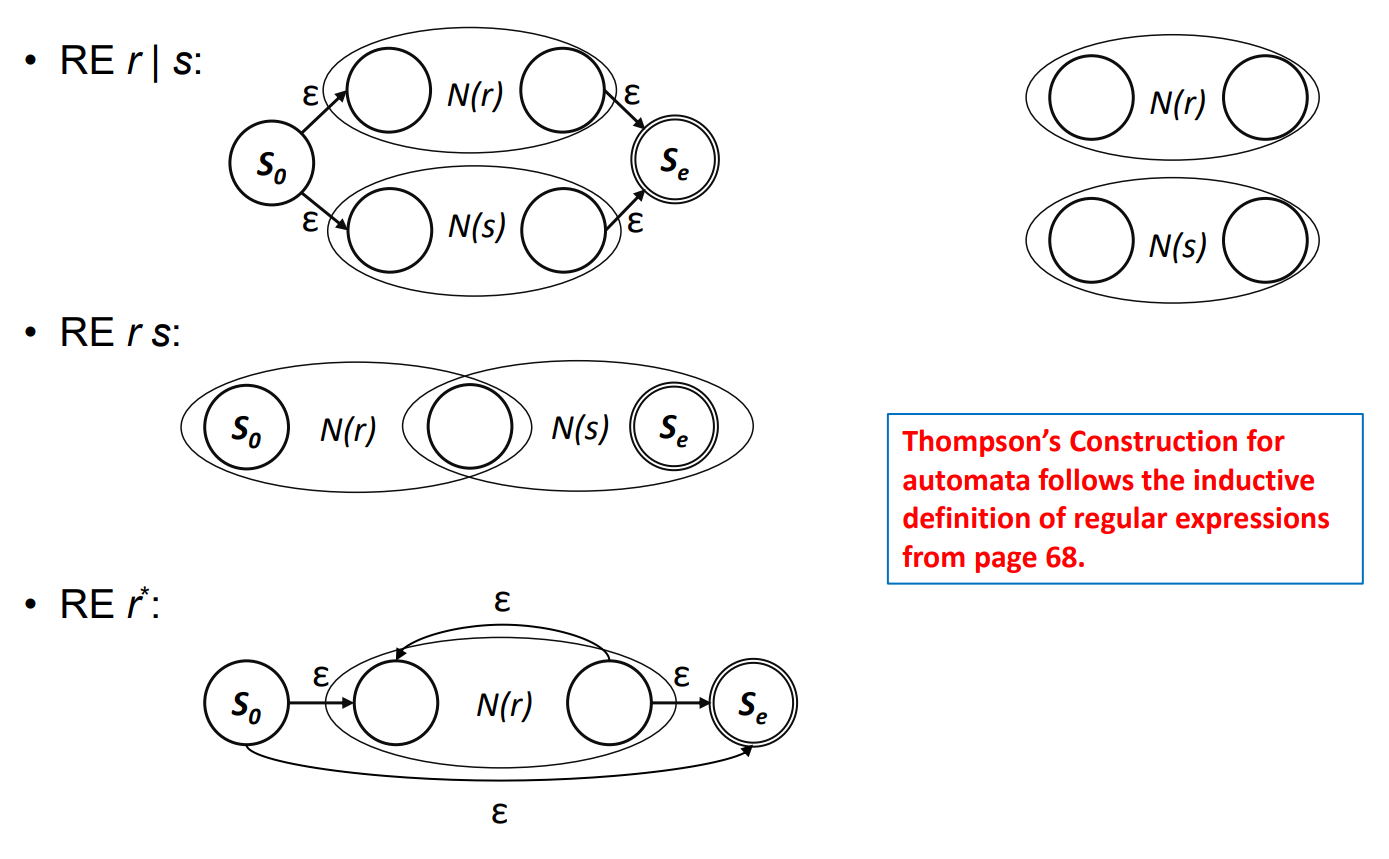
Subset Construction

NFA >> DFA

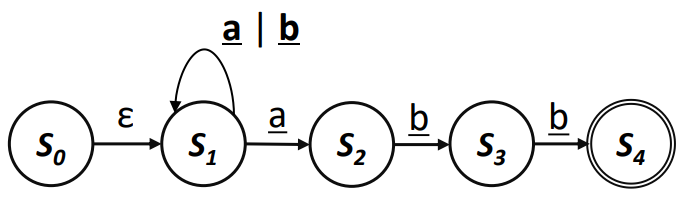
본 NFA를 DFA로 변환한다 가정한다

• $S_1$에서 입력 a를 받으면 $S_1$ 혹은 $S_2$로 이동하게 되는데 이를 둘 다 따라가는 것이다!
• $\{S_1, S_2\}$ 라는 가상 상태(Virtual State)를 이용해 이를 DFA로 변환한다!

만약 $\{S_1, S_2\}$ 상태에서 b를 입력받게 된다면?

• Virtual State안의 State들이 b를 받았을때 갈수 있는 모든 State를 고려해 다음 Virtual State(2개 이상 가능성) 혹은 State로 연결한다.

$\epsilon$ Transition의 상황은?

• $\epsilon$ Transition의 경우, Transition의 시작지 State와 목적지 State를 미리 합쳐 Virtual State로 만든다!

$\cdot$ $S_0$의 경우 $\epsilon$ Transition을 가졌기에 목적지 State인 $S_1$과 합쳐져 $\{S_0, S_1\}$ Virtual State가 된다.
$\cdot$ $S_0$과 $S_1$에서 각각 a를 입력 받았을때 갈수있는 목적지 State는 $S_1$ 과 $S_2$ 이기에, 이 둘을 합쳐 Virtual State로 만든다.

• 위 과정을 Initial State에서 시작해 모든 State/Virtual State의 Transition에 대해 더이상 추가할게 없을때까지 반복한다.
• State중 Accept State를 포함하는 Virtual State 혹은 그냥 Accept State는 Accept State가 된다.
• 결과적으로 생겨난 Virtual State들에 새로운 이름을 지어주면 된다.

• $Move(s_i , a)$ - $s_i$ 에서 a 입력을 받았을때 가는 State의 집합
  • Virtual State
• $ε-closure(s_i)$ - $s_i$ 에서 $\epsilon$ Transition을 만났을때 가는 State의 집합
  • Virtual State

알고리즘

Dstates : 현재 Tracking 중인 Virtual State들의 모임. 확인 후 Mark 해준다.

While Loop에 돌아가는 Dstate의 원소는 Mark 되지 않은것만

1. Initial State에서 $\epsilon$ Transition 확인

2. Dstate안에 있는 Mark되지 않은 State / VirtualState들에 대해 모든 Input의 경우로 $ε-closure(s_i)$ / $Move(s_i , a)$ 함수 돌려서 확인하기
   2.1. Transition 이후 $\epsilon$ Transition을 만날 경우까지 고려한다.
   - move >> epsilon 순서로 실행
   2.2 여기서 출발지로 사용되는 Virtual State는 미리 Mark되어 다시 While loop에 오지 않는다.
   2.3 특정 Input에 도착하는 State들의 집합을 U로 정의한다.

3. 그렇게 생긴 U라는 Virtual State가 Dstate에 없으면 < 새로운 Virtual State > Mark되지 않은 상태로 Dstate 에 추가함.

4. U 를 전이함수에 추가한다.

5. Dstate가 비면, 즉 모든 가능한 Virtual State/State의 Input이 확인이 되면 끝난다.

6. 기존 nfa의 accepting state를 가지는 모든 Virtual State / State는 Acceping State가 된다!

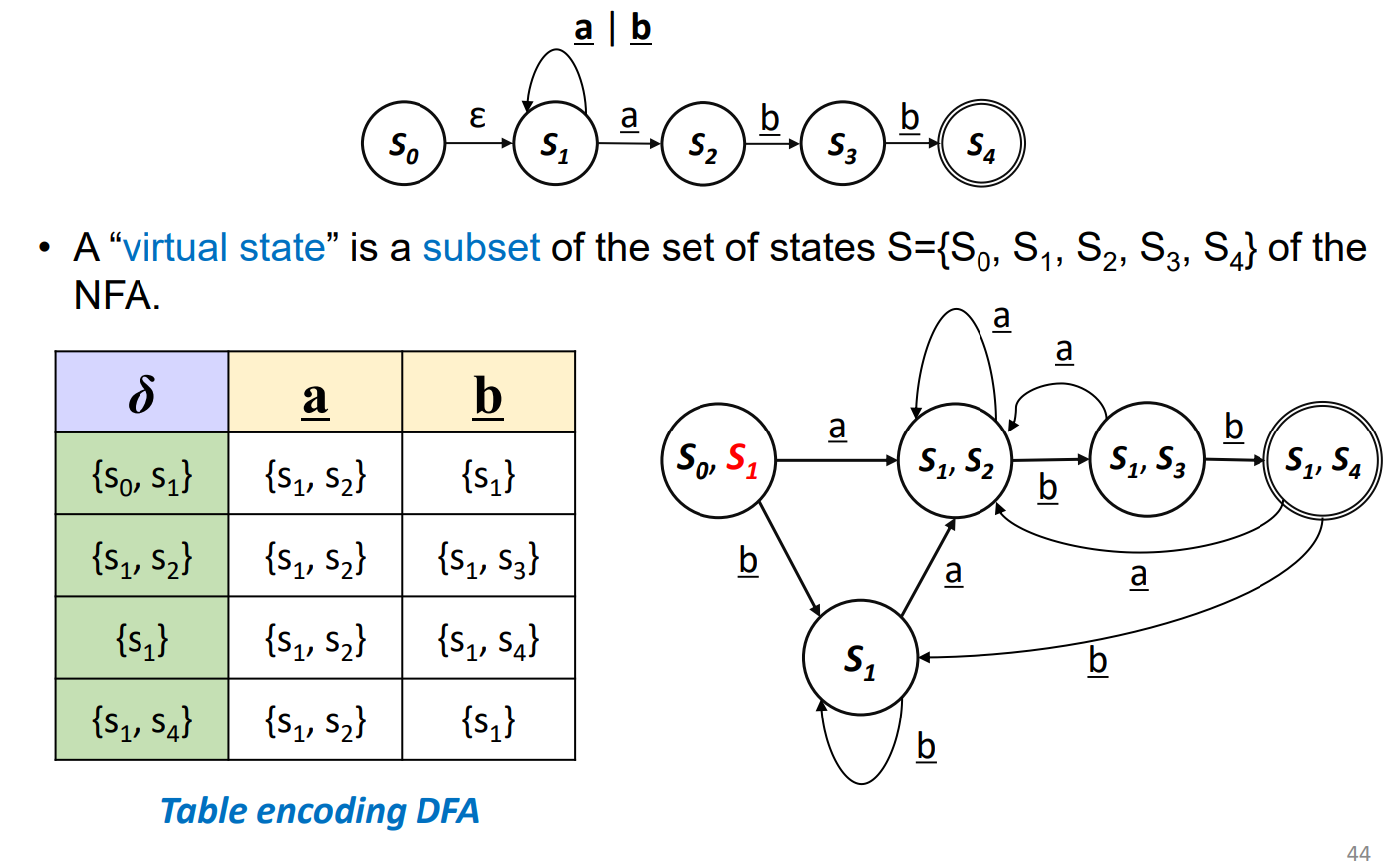
>> Next State로 가능한 모든 State를 전부 찾아내서 Virtual State로 묶어내는 과정

결과 / Result

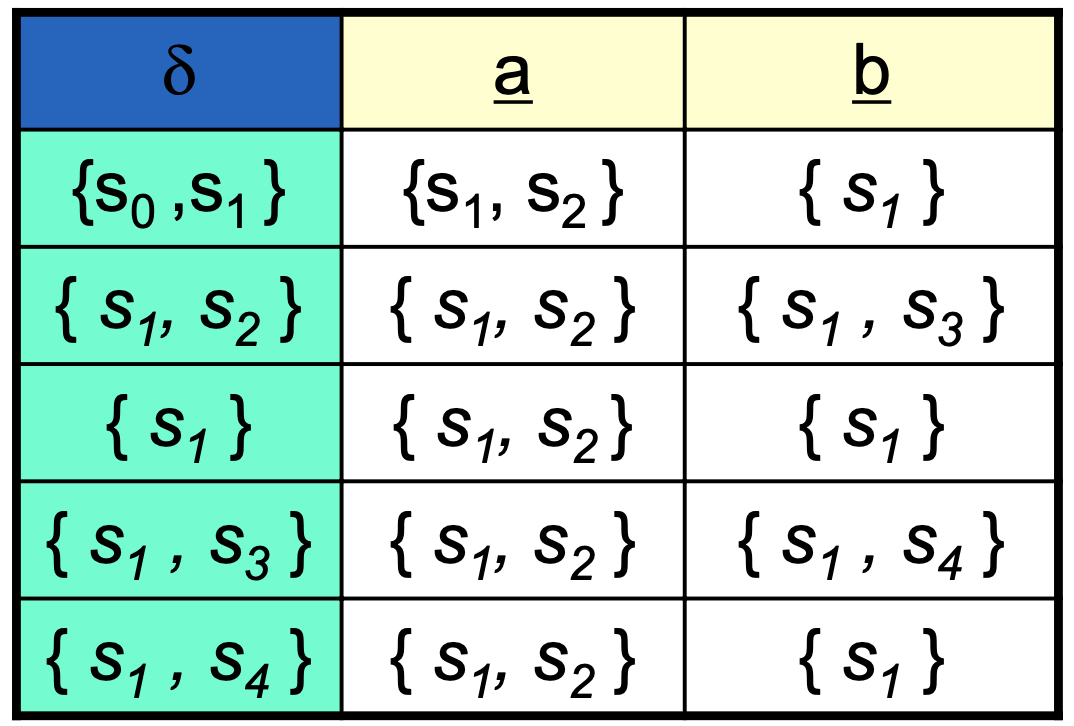
DFA 완성.

---

DFA Minimization

• Distinguishable State 찾기
• 두 State가 Distinguishable 하지 않을시 합쳐서 단일 State로 표현

Distinguishable?

• 두 State에서 w 문자열을 입력 받았을때 하나는 Accept되고 하나는 Accept되지 않는것

Not Distinguishable?

• 두 State에서 w 문자열을 입력 받았을때 둘 다 Accept 될 경우

즉, 동일한 입력에 대해 동일한 결과를 주기에 합쳐도 된다는 것.

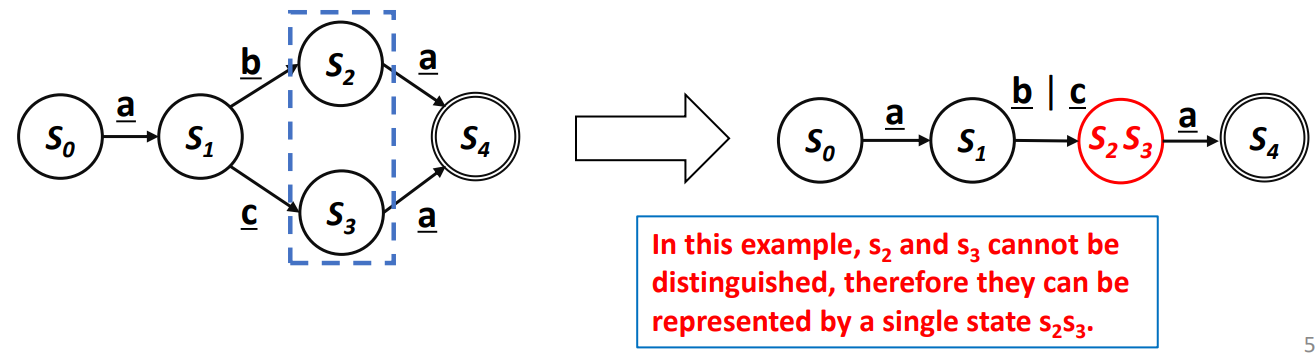
$S_2$ 와 $S_3$은 같은 "a" 입력을 받았을때 둘 다 accept 되기에($S_4$에 도달함) 둘은 합쳐질수 있다.

절차

예시

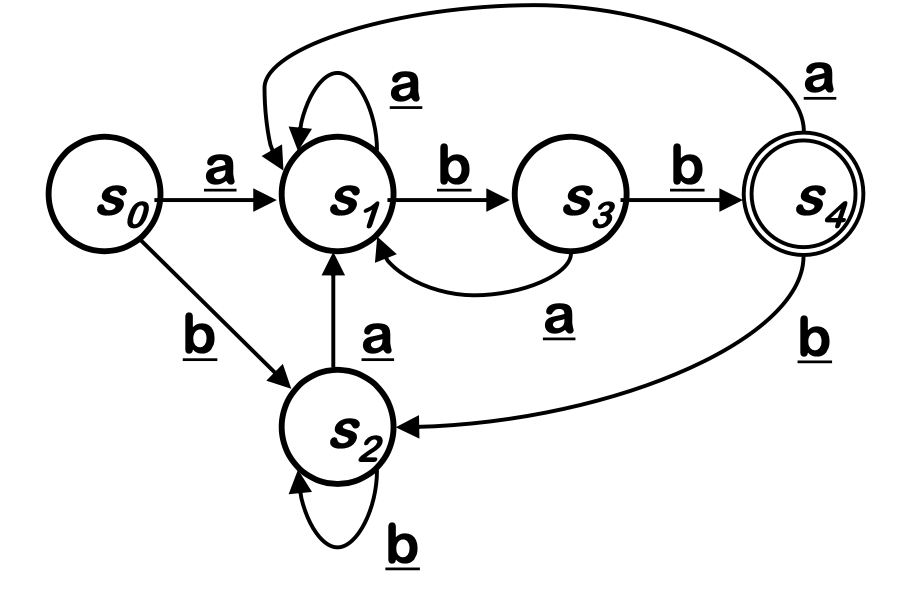
STEP 1

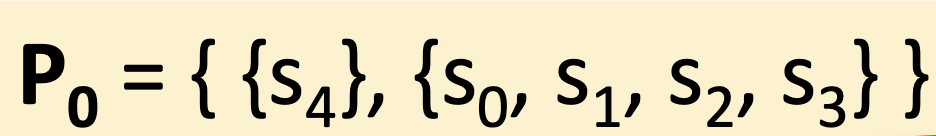
1. State(S)들을 두가지 Partition으로 분류한다.
   • Final State : F
   • Final State가 아닌것 : S - F
2. P = {S, S-F} , P는 두 집합으로 이루어진 또 다른 집합.

STEP 2

• p는 P에 포함된 파티션
• Split 함수
  • Symble A에 대해 Distinguishable 할 시< Transition 결과 서로 다른 Partition으로 이동한다.> 그를 이용해 같은 partition으로 Transition 하는 쌍 끼리 파티션을 분리 한다.
  • 그렇지 않을시 분리하지 않는다.
    - alpha 입력에 대해 파티션이 나뉘는 경우와 나뉘지 않는 경우
    - 우측 경우 빨간색 선으로 파티션이 나뉘게 된다
    
  • 이미 하나만 있는 Partition은 더이상 나뉘어 질수 없다.
  • 이를 모든 State에 반복한다.
    저기서 합집합은 새로 나뉘어진 partition 혹은 나뉘어지지 않은 파티션을 T에 추가하되, 중복되지 않게 한다는것

참고영상

• 이를 P가 더이상 변하지 않을때까지 반복한다
  • while (P is still changing)
  • old_P 를 하나 두어 관리하면 될듯 하다.
  • 결과를 이용해 DFA를 최소화한다. 여러 State가 들어간 집합은 내부 State들이 Not Distinguishable 하다는 것이다.

---

Scanner Generator

RE > NFA > DFA > Minimal DFA 자동화

C Scanner generator

• lex
• flex
• Mks lex

Java Scanner generator

• Jlex
• Jflex
• JavaCC

JLex

user code // copied verbatim to the scanner file
%%
JLEX directives (declarations)
%%
regular expression rules

• 유저코드 < 위엔 없음 >
• 알파벳 정의
• RE 정의 및 토큰 정의

---

Regex의 한계

• Regex의 경우 정확히 n번만 반복하게 할수 없다.
  Ex. $0^n1^n$ : 0이 n번, 또 1이 정확히 n번 반복하게 한다.
• counting을 고려하지 않기 때문이다.

Regex와 Context-Free-Grammar

• Regex는 CFG보다 덜 Formal하다.
• 모든 Regex는 CFG로 표현 가능하고, 모든 CFG는 Regex로 표현할수 없다.
• Regex로 표현 가능한 언어는 Regular language라 부른다.