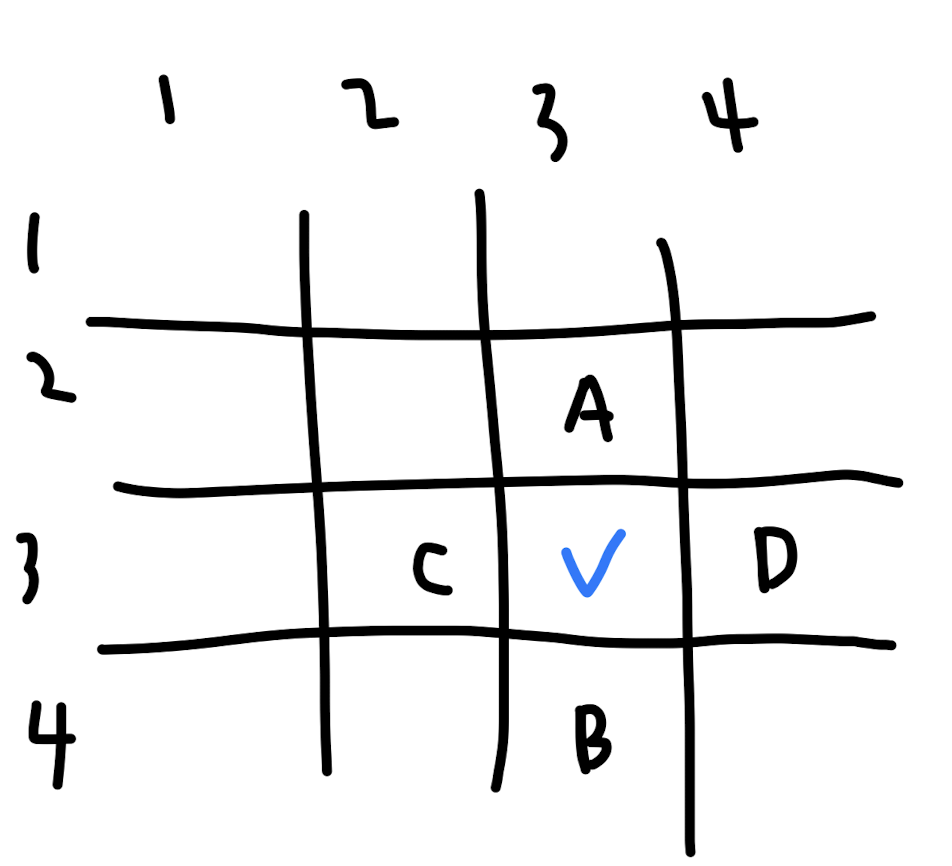
1090 - 체커
풀이 참고 - 2주만에 통과하는 알고리즘 코딩테스트 (2024년)
코테에서 다 물먹은 나...
코테에서 다 떨어질 것만 같아서(맞긴하다.) 서류를 쓸 의지도 안생길 지경
심기일전해서 강의를 들을려고 하는데...
코테를 보고, 준비하면서 참 완탐과 구현이 중요하다고 생각한다.
왜냐면 내가 최근 연달아 본 3개의 코테에서 모두 다 완탐 + 구현에서 뭔가 한두개씩 삐끗, 혹은 풀이를 너무 오래 붙잡고 있어서 터졌기 때문이다.
여하튼 강의를 들으면서 풀이를 생각하기도 어려웠고, 내가 항상 사고하면서 생각하지 못하는 부분을 후벼파는 문제라 따로 정리하고자 한다.
문제 설명
https://www.acmicpc.net/problem/1090
(x,y)인 n개의 체커가 주어져 있고, 체커를 움직여서 특정 한 칸에 k개의 체커를 모이도록 해야한다. (k는 1 ~ n) 이다.
첫번째 방식(틀림)
내가 처음에 생각한 방법은 x의 값들과 y의 값들의 평균을 구해가지고 각각의 x,y를 이동시킨 값을 구하는 방식이였다.
4
3 2
3 4
2 3
4 3만약 위의 예시인 경우에는 x는 3, y도 3이 나온다.
좌표평면을 그려보면 정답이다.
나와있는 예제들도 다 잘된다.
하지만 반례가 있으니...
4
3 2
3 4
2 101
4 101이렇게 되면 x는 3, y는 52가 나와버린다.
2개의 체커가 모이도록 하는데 고작 2만([3,2],[3,4]) 이동하면 되는데, 이렇게 되면 y가 50은 넘게 이동해야한다.
두번째 방식(틀림)
이렇게 생각하게 된 것은
1. x,y좌표가 각각 1,000,000보다 작거나 같은 수이다.
2. 음... x,y좌표 전부 다 완탐을 돌리진 못하겠담
3. 그러면 x,y 각각의 최대값과 최소값만 돌려볼까?
라는 아이디어에서 시작했다.
# 메모리 초과나는 풀이
import sys
n = int(input())
xl = []
yl = []
for _ in range(n):
x,y = map(int,input().split())
xl.append(x)
yl.append(y)
dis = [] # 각 좌표에 대한 거리의 차가 들어있는 변수
xn = max(xl) - min(xl) + 1
yn = max(yl) - min(yl) + 1
for i in range(min(xl),max(xl)+1):
for j in range(min(yl), max(yl) + 1):
dis.append([0]*n)
a = 0
for i in range(xn):
for j in range(yn):
for k in range(n):
dis[a][k] = abs(xl[k] - (min(xl) + i)) + abs(yl[k] - (min(yl) + j))
a += 1 # dis에 담기위해...
ans = [999999999] * n
for k in range(n):
for j in dis:
jl = sorted(j)
if ans[k] > sum(jl[:k+1]):
ans[k] = sum(jl[:k+1])
print(*ans)이 코드는 전형적인 나의 고질병인 무식한 완탐 + 엄청 긴 리스트 남발형 풀이인데 메모리 초과가 떴다.
# 시간초과
import math
n = int(input())
xl = []
yl = []
for _ in range(n):
x, y = map(int, input().split())
xl.append(x)
yl.append(y)
ans = [math.inf] * n
for i in range(min(xl), max(xl) + 1):
for j in range(min(yl), max(yl) + 1):
current_distances = []
for k in range(n):
distance = abs(xl[k] - i) + abs(yl[k] - j)
current_distances.append(distance)
current_distances.sort()
for k in range(n):
ans[k] = min(ans[k], sum(current_distances[:k + 1]))
print(*ans)역시나... 시간초과가 뜬다.
생각해보면 최악의 경우가 x,y 각각 100000개씩 가능하니 당연히 시간초과가...ㅠ
세번째 방식(맞음)
강의를 들으며 계속 궁금한 풀이가 있었는데 '우리의 집 중에 한 곳만 구하면 된다' 이거 였다.
아까는 x와 y의 최소, 최대 사이의 값을 다 구해보는 것이였는데, 이제는 아예 x,y의 좌표가 있는 값들에 대한 최소값만 확인하겠다는 거다.
각 좌표에 대한 값들만 확인해도 각 좌표에 대한 거리 비용만큼은 최소값이 나온다.
1차원으로 생각해보면
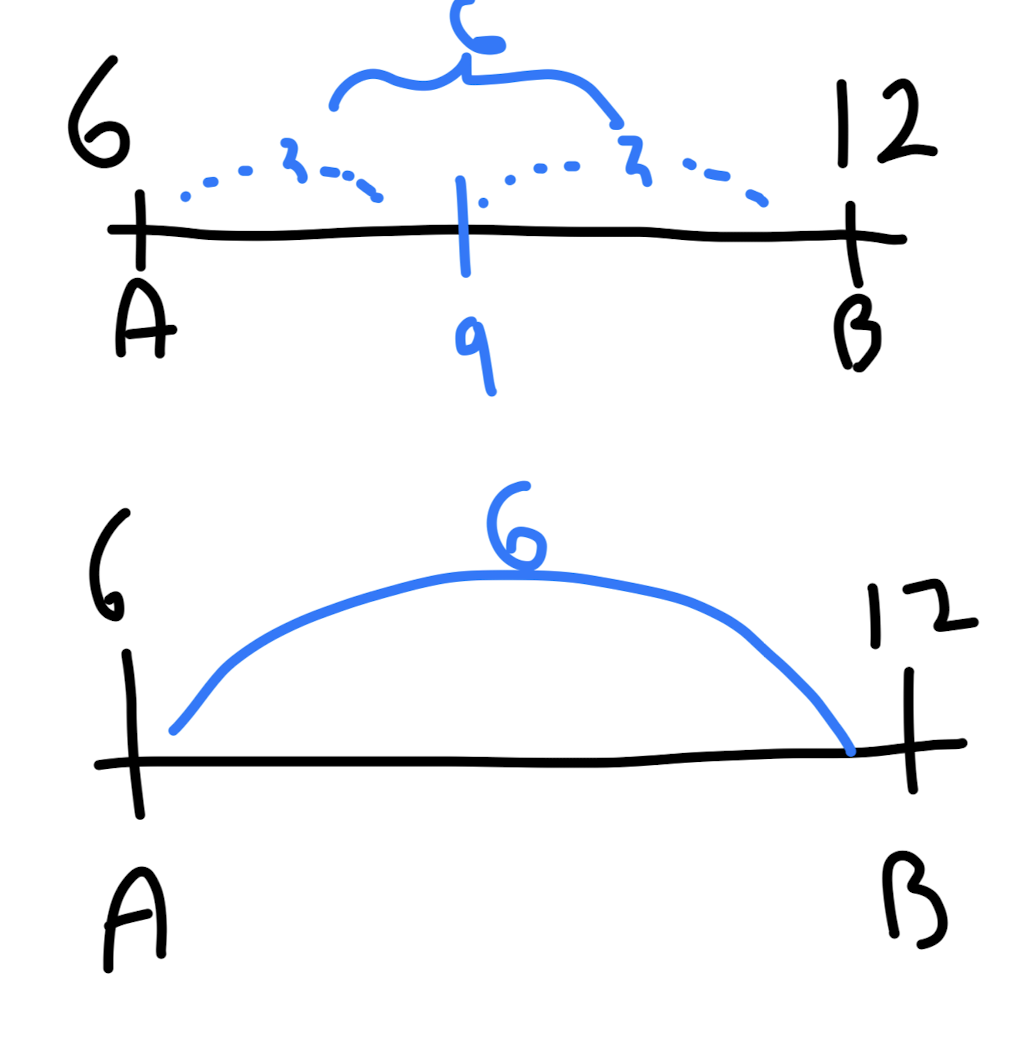
중간에 9를 넣으나 a에서 시작하나 b에서 시작하나 6인 것은 매한가지이다.
이걸 2차원으로 확장시켜 생각해보면 역시나... 그냥 그 좌표에서 시작해도 된다는 것을 알 수 있다. 이거 뭐 말로 표현을 못하겠다..ㅠ 좌표평면을 그려봐야 그나마 이해가 된다.
import math
n = int(input())
xl = []
yl = []
arr = []
ans = [math.inf]*n
for _ in range(n):
x,y = map(int,input().split())
arr.append([x,y])
xl.append(x)
yl.append(y)
l = []
for x in xl:
for y in yl:
dis = []
for nx, ny in arr:
dis.append(abs(nx - x) + abs(ny-y))
dis.sort()
for i in range(len(dis)):
d = sum(dis[:i+1])
if ans[i] > d:
ans[i] = d
print(*ans)각각의 거리에 대해 연산을 다 하고 나서 또 다시 최소 값을 구하는 것이 아니라
각각의 거리에 대해 연산을 하면서 최소값을 구할 수 있다.
참고로 문제를 풀다보면 각 좌표에 대한 최소값만 구하면 되는거 아닌가 싶을 수 있는데 바로 밑의 예시를 보면 아니라는 것을 알게된다. 3,3가 적합한데도 좌표끼리만 최소 값을 비교하기 때문이다.