최대공약수, 최소공배수

어라라... 초등수준의 수학을 기억 못하는 사람이 있나요..?

그게 바로 나였습니다.

분명 대학교 막 입학했을 땐 이런 건 금방금방 풀었는데, 왜 지금 와서는 못하는 걸까..?

일단 다시 기억해 보고자 정리해 보도록 하자.

최대공약수

a, b가 있고 각각 156, 60이라고 가정한다.
a, b 모두를 만족시키는 약수를 공약수라고 한다. 이 공약수들 중 가장 큰 값을 최대공약수라고 한다.

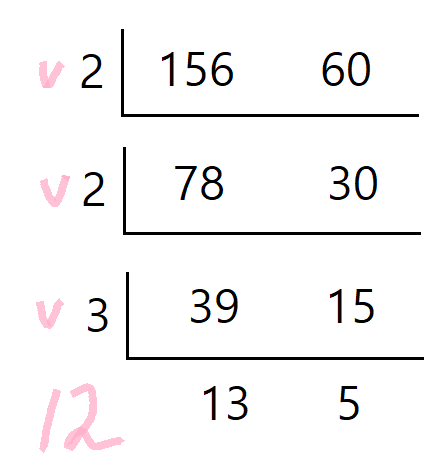
여기서는 2 x 2 x 3이라 최대공약수가 12이다.

최소공배수

공배수는 두 개 이상의 자연수의 공통적인 배수라고 한다. a의 배수이기도 하고 b의 배수이기도 해야 하는 수이다. 최소공배수는 이러한 공배수들 중에 가장 작은 수이다.

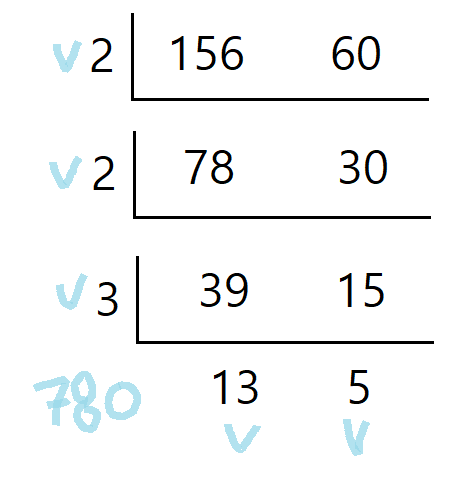
여기서는 2 x 2 x 3 x 13 x 5 해서 최소공배수가 780이다.

최대공약수를 gcd라고 하고, 최소공배수를 lcm이라고 표현하고 이는 파이썬의 math 라이브러리에서도 같은 표현으로 사용한다.

그리고 a x b = gcd(a,b) x lcm(a,b)와 같다.

유클리드 호제법

최대공약수를 구하는 알고리즘이다.
자연수 a가 b보다 클 때 a, b에 대해서 a를 b로 나눈 나머지를 r이라고 하면, a와 b의 최대공약수는 b와 r의 최대공약수와 같다. 이 과정을 반복하다가 나머지가 0이 되었을 때 나누는 수가 a, b의 최대공약수이다.

사실 말보다는 밑에 그림을 보는 게 이해하기 쉽다.

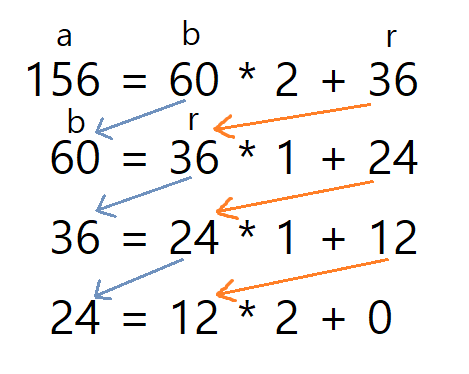
여기서 나머지가 0이 되었을 때 나누는 몫이 12이기 때문에 최대공약수는 12이다.

파이썬 코드로는?

a, b = map(int,input().split())

def gcd(a, b):
    while b > 0:
        tmp = a
        a = b
        b = tmp % b
    return a 

그러면 최소공배수는...?

두 개 이상의 자연수의 공통적인 배수 중 가장 작은 값이기 때문에 두 개의 곱을 두 개의 최대공약수로 나누면 된다.

def lcm(a, b):
    return a * b // gcd(a,b)

하지만 파이썬에서는 굳이 구현해서 사용하지 않아도 된다.

math 라이브러리

내가 주로 사용하고 있는 온라인저지 사이트는 백준과 프로그래머스인데, 실제로 코테볼 때도 주로 프로그래머스를 사용하였다.

프로그래머스의 파이썬 버전은 3.8.5이다.

3.5버전 이상이라면 math라이브러리의 gcd를 사용할 수 있다.
공식 레퍼런스 링크

또한 3.9버전부터는 lcm도 생겼다.
공식 레퍼런스 링크

하지만 위에서 보다시피 아직까진(2023년 12월) 코테에서 자주 보게되는 프로그래머스에선 3.9를 지원하지 않기 때문에 gcd만 사용하고 lcm은 직접 구현해도 좋을 거 같다.

문제 예시

백준 13241번 최소공배수
문제 링크

import math
a, b = map(int,input().split())
print(a * b // math.gcd(a,b))

백준 1735번 분수 합
문제 링크

import math
a, b = map(int,input().split())
c, d = map(int,input().split())

bottom = b * d // math.gcd(b,d)

top = bottom//b * a + bottom//d * c

print(top//math.gcd(bottom,top), bottom//math.gcd(bottom,top))