백준 1629 곱셈

https://www.acmicpc.net/problem/1629

문제해결

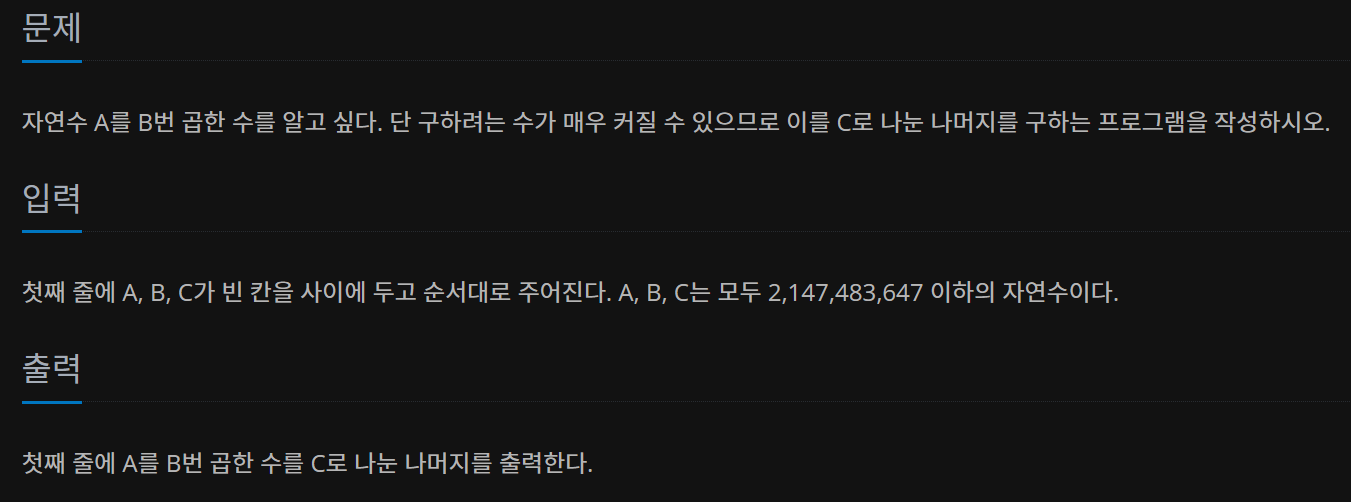
제곱의 성질과 모듈러의 성질을 알고 있다면 쉽게 풀 수 있는 문제이다.
문제에서 A, B, C 모두 2,147,483,647 이하의 자연수라고 했기 때문에 지수를 반으로 나누어 처리하면 시간복잡도는 O(logN)이 된다.

이 때, 지수가 짝수인 경우와 홀수인 경우를 나누어 생각해야 한다. 다음 예시를 보자.
10^11 = 10^5 * 10^5 * 10
10^5 = 10^2 * 10^2 * 10
10^2 = 10^1 * 10^1

즉, 지수가 짝수인 경우 밑^지수/2 * 밑^지수/2
지수가 홀수인 경우 밑^지수/2 * 밑^지수/2 * 밑 형태임을 알 수 있다.

소스코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

/**
 * Math 클래스의 pow 메소드를 이용해서 풀려고 했으나 틀림
 * 제곱의 성질을 이용하여 분할정복으로 풀이 -> 시간복잡도 O(logN)
 * 힌트 : 지수를 2로 나눔
 */

public class b1629 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        long a = Long.parseLong(st.nextToken());
        long b = Long.parseLong(st.nextToken());
        long c = Long.parseLong(st.nextToken());
        System.out.println(func(a, b, c));
    }

    public static long func(long a, long b, long c) {
        // b가 1일 때
        if (b == 1) {
            return a % c;
        }   
        long temp = func(a, b / 2, c);
        // b가 홀수일 때
        if (b % 2 == 1) {
            return (temp * temp % c) * a % c;
        }
        // b가 짝수일 때
        return temp * temp % c;
    }
}

회고

처음에 시간복잡도를 고려하지 않고 단순하게 Math 클래스의 pow 메소드를 이용하여 풀이하였다. 연속된 틀렸습니다 받고 제곱의 성질과 모듈러의 성질에 대한 힌트를 얻어서 해당 문제를 해결했다. 여러 번의 시도 끝에 성공!

초기코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class b1629 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        long a = Long.parseLong(st.nextToken());
        long b = Long.parseLong(st.nextToken());
        long c = Long.parseLong(st.nextToken());
        long result = 0;
        result = (long) Math.pow(a, b);
        System.out.println(result%c);
    }
}