백준 18352 특정 거리의 도시 찾기

https://www.acmicpc.net/problem/18352

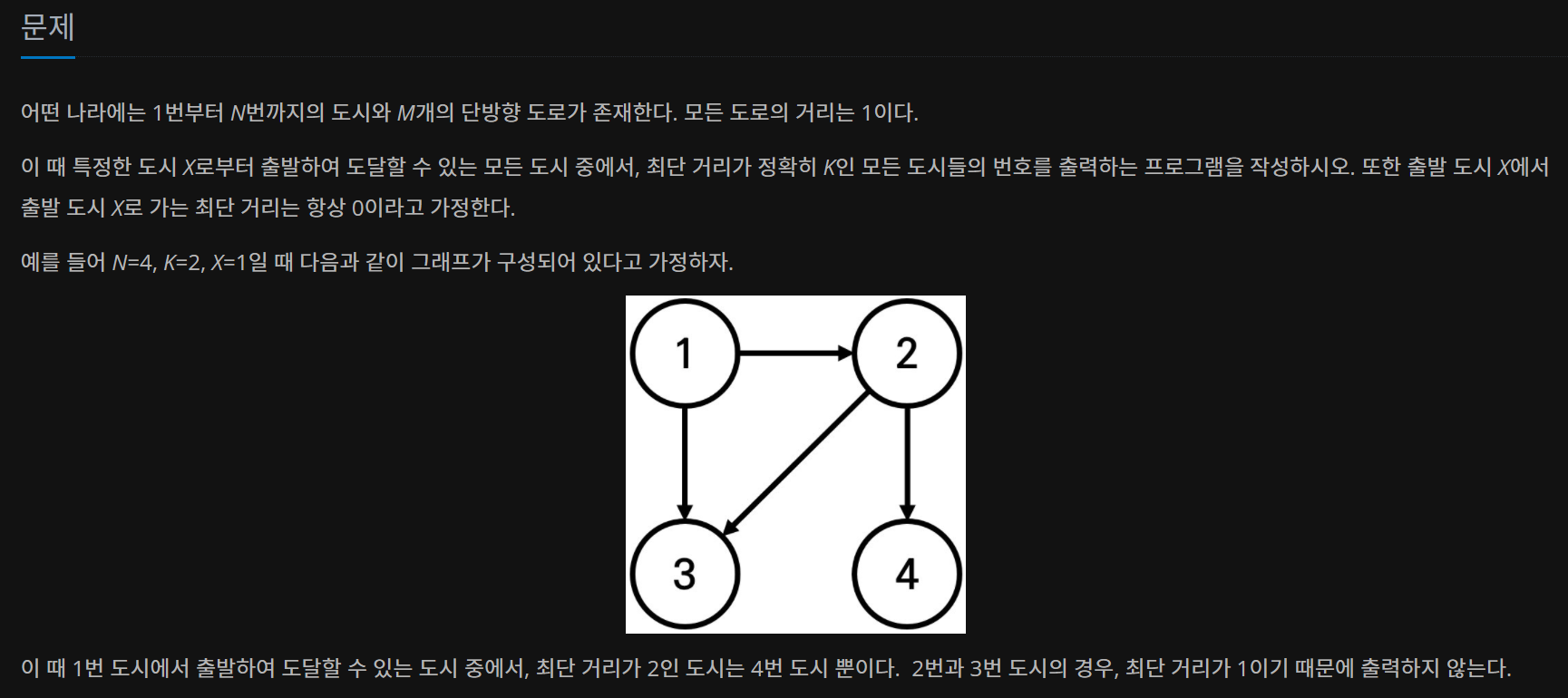
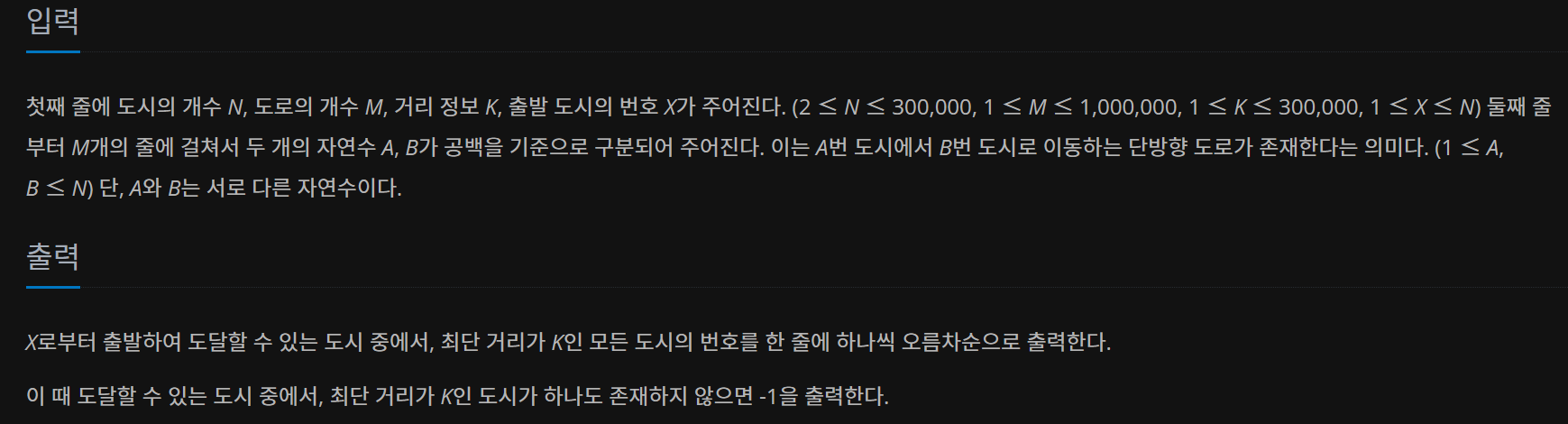
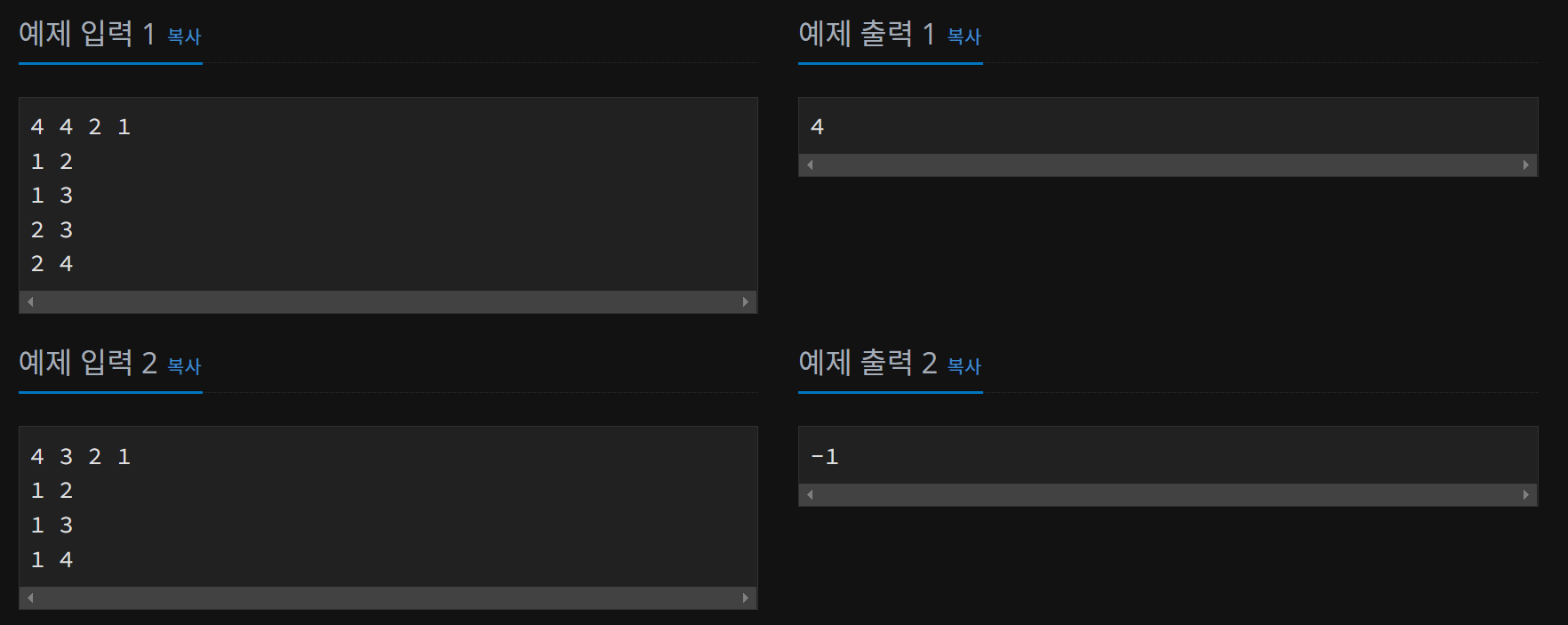
문제해결

그래프는 인접 행렬과 인접 리스트 두 가지로 표현할 수 있다.
먼저, 인접 행렬과 인접 리스트의 개념에 대해 알아보자.
인접 행렬이란 2차원 배열로 그래프의 연결 관계를 표현하는 방식으로 모든 관계를 저장해서 노드의 개수가 많을수록 불필요한 메모리가 낭비된다.
인접 리스트란 리스트로 그래프의 연결 관계를 표현하는 방식으로 연결된 정보만을 저자하기 때문에 메모리를 효율적으로 사용한다. 그러나 인접 행렬 방식에 비해 특정한 두 노드가 연결되어 있는지에 대한 정보를 얻는 속도가 느리다.

해당 문제는 간선 개수가 적어서 인접 리스트 방식으로 출발 도시로부터 최단 거리가 k인 도시 정보를 구하였다.

1. 인접 리스트 선언
2. 거리에 대한 정보 배열 d 선언하고 -1로 초기화
3. 출발 도시 x에서 출발 도시 x로 가는 최단 거리는 항상 0
4. bfs 탐색으로 이동할 수 있으면서 아직 방문하지 않은 도시의 최단 거리 갱신
5. 최단 거리가 k인 도시가 여러 개일경우 오름차순으로 출력
6. 최단 거리가 k인 도시가 하나도 없으면 -1 출력

나중에 찾아보니까 다익스트라로 푸는 방법도 있었는데 다익스트라에 대해 공부하지 못했고 모든 도로의 거리가 1(간선의 가중치 = 1)이기 때문에 bfs로 풀어도 되는 문제라고 한다!

소스코드

package search;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;

public class b18352 {
    static int n, m, k, x;
    // 인접 리스트
    static ArrayList<ArrayList<Integer>> graph = new ArrayList<>();
    static int[] d = new int[300001]; // 모든 도시에 대한 최단 거리 초기화

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        n = Integer.parseInt(st.nextToken());
        m = Integer.parseInt(st.nextToken());
        k = Integer.parseInt(st.nextToken());
        x = Integer.parseInt(st.nextToken());
        for (int i = 0; i <= n; i++) {
            graph.add(new ArrayList<Integer>());
            d[i] = -1;
        }
        /**
         * graph[0]
         * graph[1] -> 2 -> 3
         * graph[2] -> 3 -> 4
         */
        for (int i = 0; i < m; i++) {
            st = new StringTokenizer(br.readLine());
            int a = Integer.parseInt(st.nextToken());
            int b = Integer.parseInt(st.nextToken());
            graph.get(a).add(b);
        }
        d[x] = 0; // 시작 도시 거리는 0
        Queue<Integer> queue = new LinkedList<>();
        queue.offer(x);
        while (!queue.isEmpty()) {
            int now = queue.poll();
            // 현재 도시에서 이동할 수 있는 모든 도시 탐색
            for (int i = 0; i < graph.get(now).size(); i++) {
                int nextNode = graph.get(now).get(i);
                // 아직 방문하지 않은 도시인 경우
                if (d[nextNode] == -1) {
                    // 최단 거리 갱신
                    d[nextNode] = d[now] + 1;
                    queue.offer(nextNode);
                }
            }
        }
        // 최단 거리가 k인 모든 도시의 번호 오름차순으로 출력
        boolean check = false;
        for (int i = 1; i <= n; i++) {
            if (d[i] == k) {
                System.out.println(i);
                check = true;
            }
        }
        // 최단 거리가 k인 도시가 없을 경우 -1 출력
        if (!check) {
            System.out.println(-1);
        }
    }
}