백준 9095 1, 2, 3 더하기

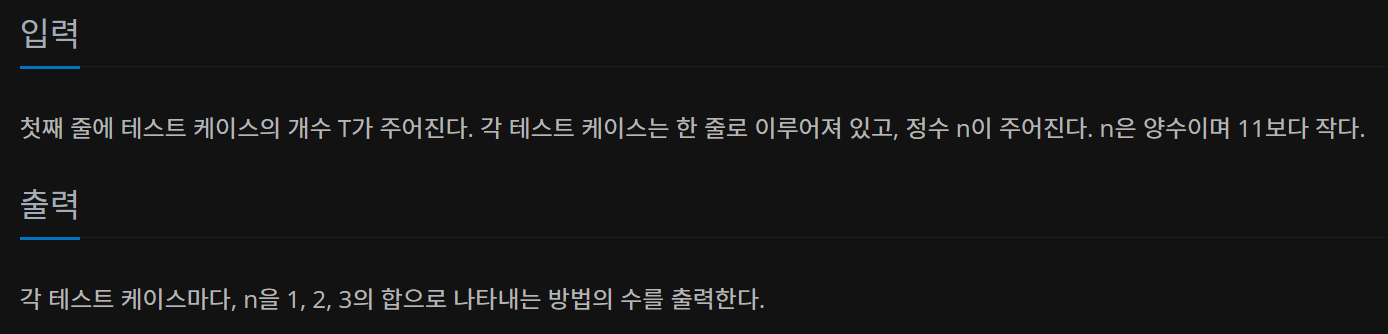
https://www.acmicpc.net/problem/9095

문제해결

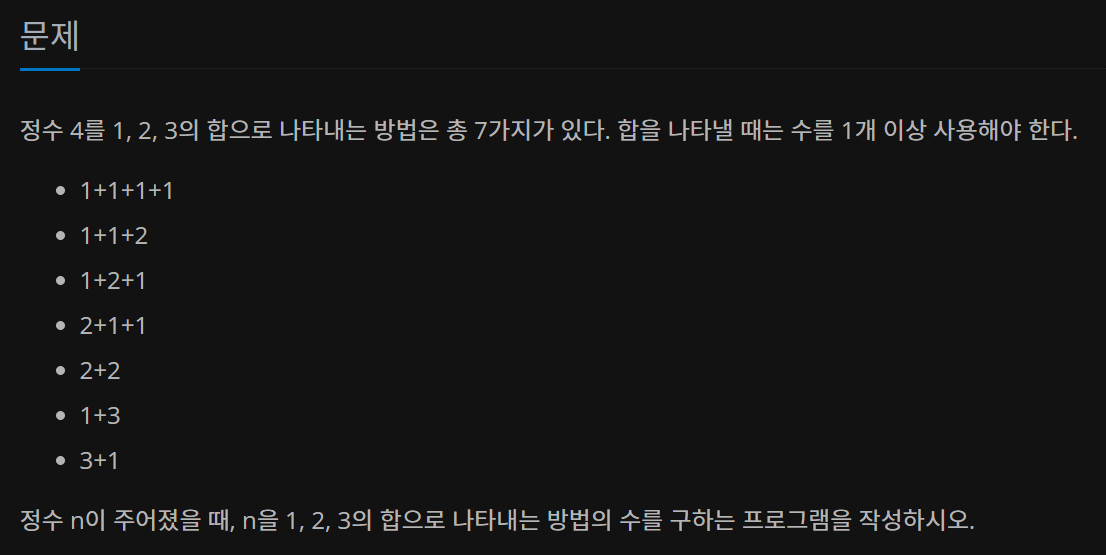
대표적인 다이나믹 프로그래밍 문제 중에 하나인 1, 2, 3 더하기 문제이다.
먼저 문제로부터 점화식을 찾았다. (난이도가 낮을수록 문제를 통해 쉽게 점화식을 찾을 수 있다고 한다.)
D[n] = 정수 n이 주어졌을 때, n을 1, 2, 3의 합으로 나타내는 방법의 수

마지막 수에 집중해보자.
1, 2, 3의 합으로 나타낼 수 있으니 마지막 수가 1인 경우 마지막 수 이전까지의 합은 n-1이 되고 마지막 수가 2인 경우 마지막 수 이전까지의 합은 n-2가 된다. 3의 경우도 마찬가지로 마지막 수 이전까지의 합은 n-3이 된다.
따라서 점화식은 D[n] = D[n-1] + D[n-2] + D[n-3] 이 된다.

점화식을 찾고 나면 초기값을 설정해줘야하는데 D[0]의 값은 얼마가 될까?
D[0]은 0을 1, 2, 3의 합으로 나타내는 방법의 수를 의미하는데 이 값은 공집합으로 1이 된다.
다음으로 D[1]은 1을 1, 2, 3의 합으로 나타내는 방법의 수로 1이 된다.
이와 같은 방법으로 D[2] = 1+1, 2 -> 2, D[3] = 1+1+1, 1+2, 2+1, 3 -> 4가 된다.

시간복잡도는 각각의 합을 구하는거라서 O(N)이 된다.

처음 DP 문제를 마주했을 때 이전과는 다른 유형에 당황했고 생각보다 짧았던 코드에 당황했다. 점화식을 찾는데 아직 익숙하지 않지만 계속 풀다보면 익숙해지겠지!

소스코드

public class b9095 {
    static int[] d;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        int t = Integer.parseInt(br.readLine());
        while (t-- > 0) {
            int n = Integer.parseInt(br.readLine());
            d = new int[11]; // n은 양수이며 11보다 작음
            d[0] = 1; // 공집합도 집합임 -> 개수 1
            d[1] = 1;
            d[2] = 2;
            d[3] = 4;
            for (int i = 4; i < d.length; i++) {
                d[i] = d[i - 1] + d[i - 2] + d[i - 3];
            }
            bw.write(d[n] + "\n");
        }
        bw.flush();
        bw.close();
    }
}