피보나치 수열 시간복잡도

재귀함수의 대표적인 예로 피보나치 수열이 있다. 시간복잡도에 대해 크게 고민해보지 않았는데 공부하다가 문득 궁금해져서 피보나치 수열의 시간복잡도를 재귀, 동적 프로그래밍, 반복문으로 비교해보고자 한다.

피보나치 수열은 첫째, 둘째항은 1이고 그 다음 항부터는 이전 항 2개를 더한 값으로 이루어진 수열이다.

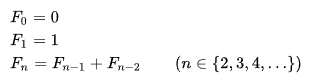
위의 점화식에 따라 계산된 피보나치 수열은 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... 다음과 같다.

1. 재귀함수

재귀함수는 자기 자신을 다시 호출하여 작업을 수행하는 방식의 함수를 의미하며 반드시 종료조건이 있어야 한다.

public static int fibo(int x) {
        if (x <= 1) {
            return x;
        } else {
            return fibo(x - 1) + fibo(x - 2);
        }
    }

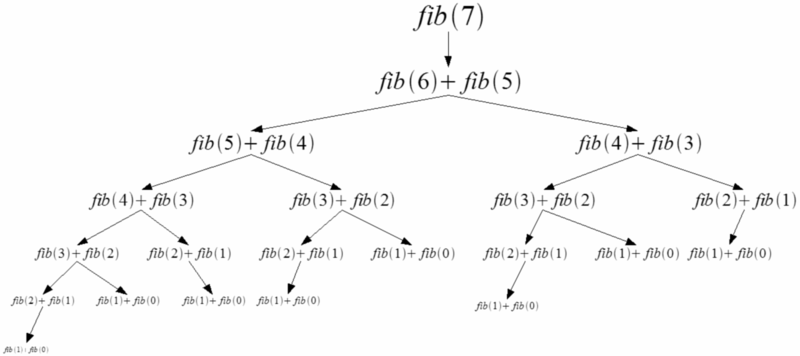
해당 그림에서 알 수 있듯이 이미 계산된 값을 다시 계산하여 시간복잡도는 O(2^n)이 된다. 또한 재귀함수의 경우 자기 자신을 호출할 때 스택에 계속 쌓이게 되는데 재귀가 깊을 경우 제한된 메모리 범위를 벗어나면 런타임 에러가 발새한다.

2. 동적 프로그래밍

동적 프로그래밍은 이전에 구해놓은 값을 이용하여 구하는 방식으로 피보나치 수열을 동적 프로그래밍으로 구현하면 O(N)의 시간복잡도를 갖는다.

private static int getDpFibo(int fiboCnt) {
   fiboDpArray = new int[fiboCnt + 1];
        
   fiboDpArray[0] = 0;
   fiboDpArray[1] = 1;
        
   if (fiboCnt > 1) {
     for (int i = 2; i <= fiboCnt; i++) {
        fiboDpArray[i] = fiboDpArray[i - 2] + fiboDpArray[i - 1];
     }
   }
        
    return fiboDpArray[fiboCnt];

3. 반복문

반복문을 이용하여 피보나치 수열을 구현하면 시간복잡도는 O(N)이다.

private static int getLoopFibo(int fiboCnt) {
    if (fiboCnt <= 1) {
        return 1;
    } else {
        int a = 0;
        int b = 1;
        int sum = 0;
        
        for (int i = 2; i <= fiboCnt; i++) {
            sum = a + b;
            a = b;
            b = sum;
        }
            
        return sum;
    }
}

Reference

• https://wedul.site/421