문제
준서가 여행에 필요하다고 생각하는 N개의 물건이 있다. 각 물건은 무게 W 와 가치 V 를 가지는데, 해당 물건을 배낭에 넣어서 가면 준서가 V만큼 즐길 수 있다. 준서는 최대 K 무게 까지의 배낭만 들고 다닐 수 있다. 준서가 최대한 즐거운 여행을 하기 위해 배낭에 넣을 수 있는 물건들의 가치의 최댓값은?
입력
첫 줄에 물품의 수 N(1<= N <= 100)과 준서가 버틸 수 있는 무게 K(1<= K <= 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1<=W<= 100,000)와 해당 물건의 가치 V(0 <= V <=1000)가 주어진다. 입력으로 주어지는 모든 수는 정수이다.
출력
한 줄에 배낭에 넣을 수 있는 최대 가치 값을 출력한다.
🔑 풀이
마찬가지로 기본+필수 동적 계획법 문제이다.
LSC 문제 풀이와 비슷하게, 준서가 버틸 수 있는 가방의 무게를 1부터 K까지 증가시키면서 각 물건을 담을 수 있는지 없는지 여부를 확인한다.
즉, 1만큼 견딜 수 있는 가방이 있을 때, 최대 가져갈 수 있는 가치 -> 2만큼 견딜 수 있는 가방이 있을 때, 최대 가져갈 수 있는 가치....순으로 구하면서 견딜 수 있는 무게 값 K이고, 모든 물건을 고려한 마지막 경우의 값을 출력하면 된다.
그림으로 다시 살펴보자.
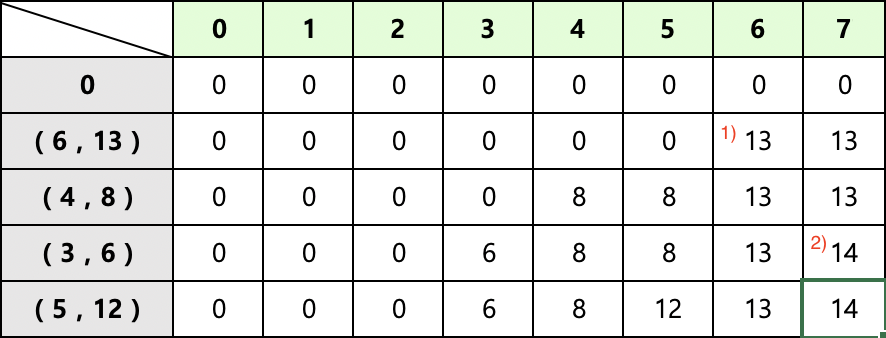
마찬가지로 2차원 행렬을 이용하여 값을 구할 것이다.
- i 는 0 ~ N ( 물건의 개수 )
- j 는 0 ~ K ( 견딜 수 있는 최대 무게 )로 둔다.
위의 그림에서는 이해 하기 편하게 물건의 ( 무게, 가치 ) 쌍으로 표현하였는데, 실제로는 값 0,1,2,..N 이다. 0번째 물건, 1번째 물건으로 생각하면 편하다.
첫번째 물건부터 차례로 가방의 무게를 1 ~ K까지 증가시키면서 최대 가져갈 수 있는 가치를 생각해보자.
-
견딜 수 있는 무게( j )가 1인 가방과 (6, 13) 인 물건
6 > 1 이므로, 가치 13을 가져가지 못한다. 그렇다면 무게가 1인 가방이 이전까지 가져올 수 있었던 최대 값인dp[i-1][j]즉, dp[0][1]의 값을 가져오면 된다. -
견딜 수 있는 무게가 2인 가방과 (6, 13)인 물건
마찬가지로 6 > 2 이므로, 해당 물건을 넣지 못한다.
견,무가 2인 가방이 최대로 가져올 수 있는 가치 값은dp[i-1][j]즉 dp[0][2]의 값을 가져온다.
이렇게 현재 견딜 수 있는 무게 j 보다 넣을 물건의 무게가 더 크다면 물건을 가져가지 못한다. 그렇다면 지금 고려하고 있는 가방의 견딜 수 있는 무게 j가 그 전까지 가져올 수 있었던 가치 값을 그대로 가져와야한다.
이전 값을 가져와야 한다고, dp[i][j-1] 값을 잘 못 생각할 수 도 있는데(나의 경우), 전이라고 한다면 무게 j인 상태에서, i번째 물건을 넣기 전인 상태이므로, dp[i-1][j] 여야 한다.
dp[i][j] = dp[i-1][j]그 다음 위의 그림의 빨간 1) 번 표시를 살펴보자.
- 견딜 수 있는 무게가 6인 가방과 (6, 13)인 물건
물건 (6, 13)을 가방이 담을 수 있으므로, 가치는 13을 가져갈 수 있다.
다만, 무게 6인 가방이 이전까지 가져 갈 수 있었던 값 dp[i-1][j] 과 비교하여 최대값을 가져가야 한다.
그 다음은 빨간 2) 번 표시를 살펴보자.
- 견딜 수 있는 무게가 7인 가방과 (3, 6)인 물건
무게 7에 물건 (3, 6)를 담을 수 있다. 가치를 6으로 가져갈 수 있음. 나머지 4 무게 만큼 더 가져갈 수 있기 때문에, 이전까지 무게 4 가방이 최대로 가져갈 수 있었던 가치 값인 dp[i-1][4] 를 더 해준다.
dp[i][j] = max(dp[i-1][j], dp[i-1][j-W]+V)🛎 패스트 캠퍼스: 알고리즘/ 자료구조 온라인 강의의 해설을 참고하였음.
- 설명이 좀 복잡하긴 한데, 한번 풀어서 쓰니까 제대로 이해할 수 있는 거 같음. 근데 놀랍게도 백준 동적계획법 1 단계 문제들이였다. 하하..내일도 1단계 문제들 풀어봐야겠다.
