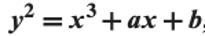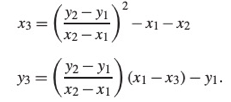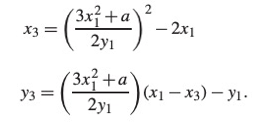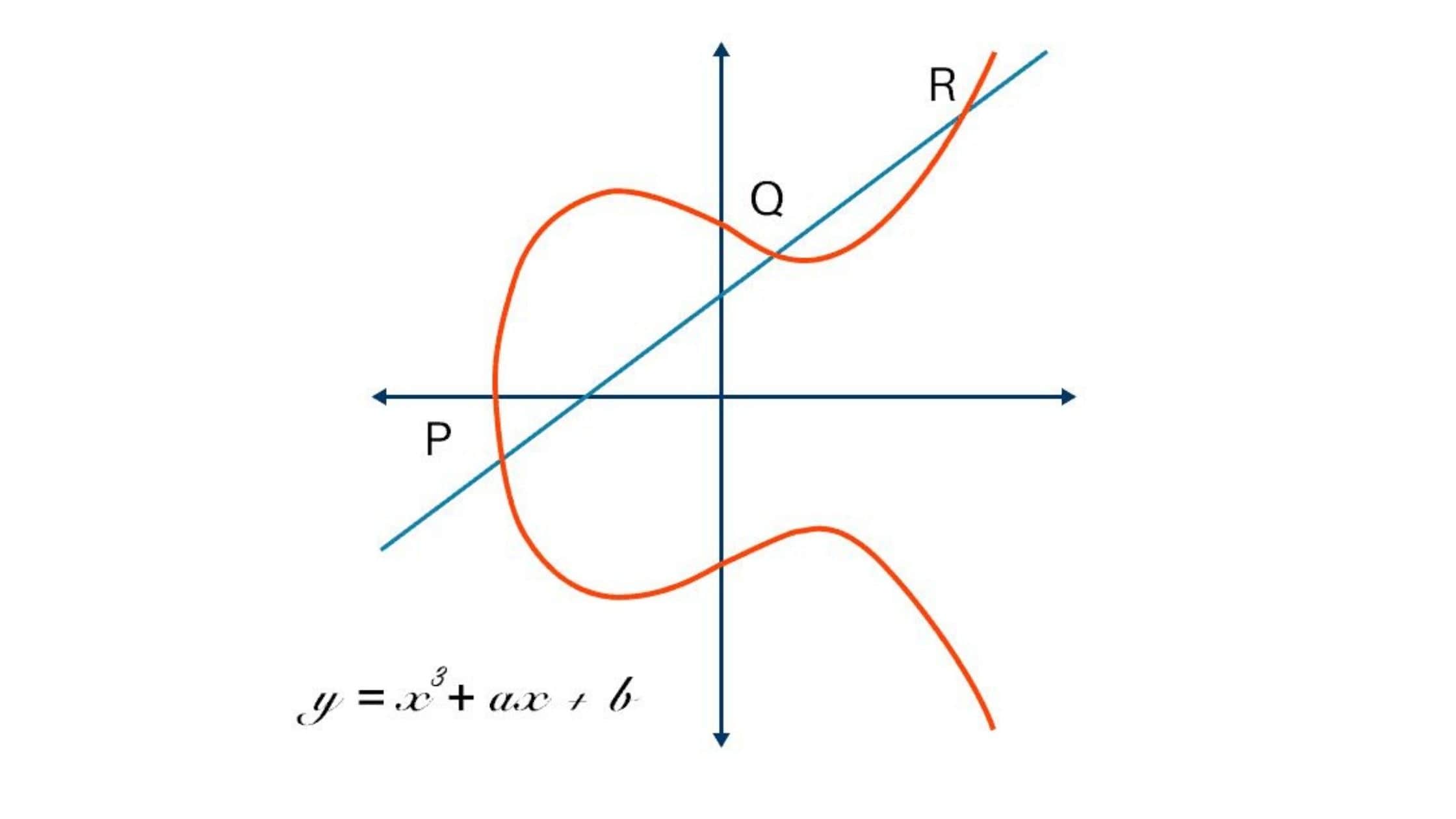
정의
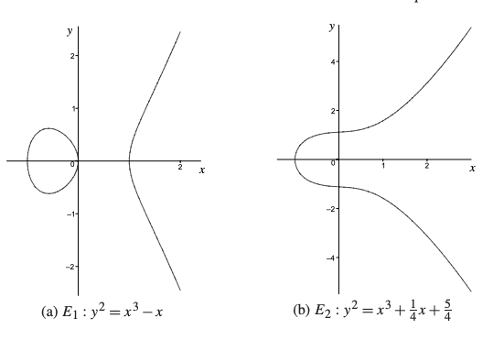
이런 꼴로 생긴 곡선을 타원 곡선이라고 합니다.
일반적으로 표현하면!이러한 식입니다.
타원 곡선을 이용해서 암호를 만들었습니다.
이 암호를 타원 곡선 암호 혹은 ECC라고 합니다.
ECC는 공개키 암호화 방식으로 쓰입니다.
타원 곡선 암호(ECC)를 사용하는 이유
공개키 암호에는 RSA라는 것이 있다. RSA암호가 깨지려면 기본적으로 소인수 분해를 해야합니다. 소인수 분해를 하는 것이 쉬운일은 아니지만 컴퓨터의 발전에 따라 소인수 분해를 하는 속도가 빨라지고 있습니다. 따라서 RSA암호가 깨지지 않으려면 RSA의 Key의 비트를 늘려야했습니다.
Key의 비트가 늘어날수록 속도는 느려집니다. 따라서 RSA보다 작은 Key로 동일한 보안수준을 보장해주는 ECC를 만들었습니다.
타원 곡선 안에서 점들의 규칙을 정의하겠습니다.
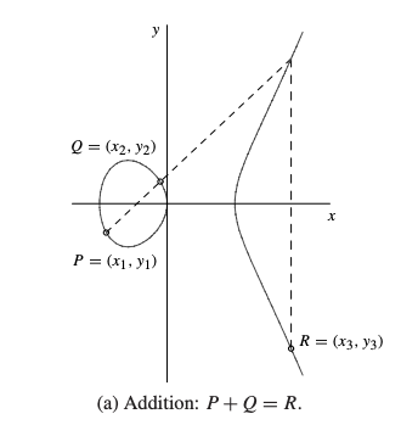
1. Addition (P+Q = R)
P 와 Q를 지나는 직선 y = mx + n과
주어진 타원곡선
을 이용해
R(x3, y3)을 구할 수 있습니다.
2. Doubling (2P = R)
점P에서의 접선의 방정식과
주어진 타원곡선
!
을 이용해 R(x3, y3)을 구할 수 있습니다.
3. ECC를 사용하는 암호 시스템
1. Key Exchange : ECDH(Elliptic Curve Diffe-Hellman)
2. Encryption / Decryption : EC ELGamal
3. Digital Signature : ECDSA(Elliptic Curve Digital Signature Algorithm)
ECC의 기본 연산과 각 시스템이 궁금하시다면
저의 GitHub를 참고해주세요.
https://github.com/imchanyang/Elliptic_Curve_Cryptography